标签:style blog http color com 使用
水平集方法由 Osher 和 Sethian 于 1988 年提出[1],最初应用于流体力学领域,后被广泛应用于各种同曲线演化相关的科学研究和工程领域。1997 年Caselles等人率先将这一理论应用到图像科学领域后,开始了基于水平集方法的图像处理技术的研究。
为了提高分割的稳健性,先后提出了基于边界边缘的几何轮廓线模型、基于区域的几何轮廓线模型、基于先验形状知识的几何轮廓线模型,纹理图像分割模型、运动图像的分割分割模型及这些模型集成化的图像分割模型。多模型成分集成是近年该学术流派发展的重要趋势。
水平集方法来解决图像分割问题就是与几何活动轮廓模型相结合,首先直接使用连续曲线来描述图像边缘,同时利用图像信息来定义某一能量泛函自变量中包括边界轮廓曲线然后应用欧拉-朗格拉日方程的动态格式来得到与该能量泛函相对应的曲线演化方程,即一类Hamilton-Jacobi方程最后应用水平集方法来模拟初始曲线沿能量下降最快的方向演化的过程,以便求得最佳的边界轮廓曲线。该方法可以归属于边缘检测的一类分割方法。
实施水平集方法的关键是界面演化的法向速度设计,通常称为速度函数。Caselles,Catte,Coll,Dibos,Malladi,Sethian,Vemuri分别基于轮廓的平均曲率运动和图像的梯度为主要成分构造水平集方法的速度函数,最早建立图像分割的几何主动轮廓线模型;
Kichenassamy,Kumar,Olver,Tannenbaum,Yezzi,Caselles,Kimmel,Sapiro基于Riemammian空间中的最小测地距离得到了经典的测地几何轮廓线模型; 这些模型皆为基于轮廓边缘的几何变形模型。上述方法的共同点是首先建立包含轮廓线(面)与图像边缘相关信息的能量泛函,使得当能量达到极小值时轮廓线正好与要分割的对象边界重合,其最速下降的速度即可做为水平集的速度函数。由于许多医学图像及卫星遥感图像等包含大量噪声,难免出现强的边缘或要分割对象的弱的边界,而该类方法主要依据边缘轮廓线处的局部信息,尽管都考虑增加常速度项进行改善,但效果有限,其自然的改进是充分考虑区域信息。(ITK中的水平集类)
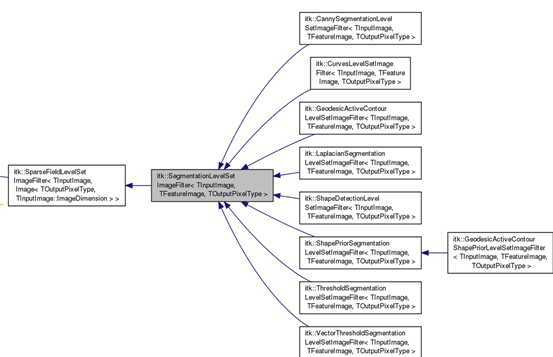
以变分方法为框架综合考虑区域信息的经典的图像分割模型是Mumford-Shah模型,Mumford-Shah泛函包括三个部分,其一是表达模型数据与观测数据相近程度的数据项,其二是表达区域内部数据平滑的平滑项,其三是约束模型轮廓长度最小的长度约束项。其中,前两项基于区域信息,第三项基于轮廓线信息。由于理论分析和实际应用的困难,在具体使用时均做不同的近似或简化。其一是用定义在Sobolev空间中规则的泛函序列近似原泛函,使得在Γ收敛的意义下新的泛函序列收敛到原泛函。
Chan-vese针对分段常值图像,基于简化的Mumford-Shah模型和水平集方法提出了不含梯度项的主动轮廓线模型,该模型的原理与Yezzi,Tsai,Willsky提出的两相与三相图像分割的统计方法非常相似,而后者不仅考虑不同区域的平均图像强度,并考虑了不同区域的平均标准差。集成区域和边界信息的经典模型还有Zhu,Yuille的融合主动轮廓线模型、区域增长模型、能量模型/Bayes模型/最小描述长度模型的区域竞争模型和Paragios基于测地主动轮廓线模型与最大后验概率的测地主动区域模型,Sifakis,Garcia,and Tziritas提出的Bayes模型和水平集方法结合的图像分割模型。
?
上述基于区域的几何变形模型或者假定要分割的图像为分段常值,或者假定不同区域的图像强度符合Gauss分布。实际上,通过不同的图像获取设备获取的图像,甚至相同的设备在不同环境下获取的图像,其分布模型可能不同。Sarti,Corsi,Mazzini,采用最大似然估计建立了符合分布的超声图像的分割方法。
区域信息的融合增强了模型的稳健性。但当将要分割的对象部分被遮挡或部分缺损时,即使边界和区域信息融合的变形模型亦无法分割得到正确的结果。先验形状知识的融合不仅能有效克服该困难,并且能够进一步改善变形模型的性态。以变分水平集为框架,在基于轮廓的能量或基于区域的能量函数基础上集成先验形状能量的相关的研究
计划:怎样学习在图像分割中水平集算法,布布扣,bubuko.com
标签:style blog http color com 使用
原文地址:http://www.cnblogs.com/taopanpan/p/3806216.html