标签:style class blog code http color
题目:输入n个整数,找出其中最小的K个数
方法一:直接std::sort,T(n) = O(nlgn)
方法二:直接std::nth_element T(n) = O(n) 但是修改了原数组
void MinKth(std::vector<int>& num, int kth, std::vector<int>& result) { if (num.size() == 0 || || kth <= 0 || kth > num.size()) { throw std::invalid_argument("invalid_argument"); } std::nth_element(num.begin(), num.begin() + kth - 1, num.end()); for (int i = 0; i < kth; ++i) { result.at(i) = num.at(i); } }
自己实现 nth_element:
一次划分:
int Partition(std::vector<int>& num, int first, int last) { if (first < 0 || last >= num.size() || first > last) { throw std::invalid_argument("invalid_argument"); } int index = rand() % (last - first + 1) + first; int key = num.at(index); std::swap(num.at(first), key); int midIndex = first; for (int i = first + 1; i <= last; ++i) { if (num.at(i) < num.at(first)) { std::swap(num.at(++midIndex), num.at(i)); } } std::swap(num.at(midIndex), num.at(first)); return midIndex; }
void GetKth(std::vector<int>& num, int kth, std::vector<int>& result) { if (num.size() == 0 || kth > num.size()) { throw std::invalid_argument("invalid_argument"); } int first = 0; int last = num.size() - 1; int index = Partition(num, first, last); while (index != kth - 1) { if (index > kth - 1) { last = index - 1; index = Partition(num, first, last); } else { first = index + 1; index = Partition(num, first, last); } } for (int i = 0; i < kth; ++i) { result.at(i) = num.at(i); } }
方法三:O(nlgk)解法
先创建一个大小为K的数据容器来存储最小的k个数,然后顺序遍历原数组:
如果容器中已有数字少于K个,则直接将原数组元素读入到容器中
如果容器中已有K个数字,表示已满,这时 我们找出容器中K个数的最大值,将这个最大值与待插入元素比较:
如果待插入元素比最大值还要大,那么直接忽略
如果待插入元素比最大值要小,那么就用这个元素替换掉最大值
我们该选取什么数据结构来表示这个数据容器呢?
如果是vector数组,那么每次找最大值需要O(k)时间,总时间为O(nk)
注意到我们每次仅仅需要的是最大值,很自然地想到最大堆,每次调整堆需要O(lgk),总时间为O(nlgk)
(1) 数据容器使用vector
void GetKth(const std::vector<int>& num, int kth, std::vector<int>& result) { if (num.size() == 0 || kth <= 0 || kth > num.size()) { throw std::invalid_argument("invalid_argument"); } for (int i = 0; i < num.size(); ++i) { if (result.size() < kth) { result.push_back(num.at(i)); } else { auto maxIter = std::max_element(result.begin(), result.end()); if (num.at(i) < *maxIter) { *maxIter = num.at(i); } } } }
(2)数据容器使用 堆
首先 堆是一棵完全二叉树,根据完全二叉树的性质,我们可以非常方便的由根节点定位到左子节点和右子节点
一般使用数组来表示完全二叉树,结点之间的关系依靠 结点编号来维持
假设父节点的编号为 index (1<= index <= num.size() ) 其左子节点编号为 2*index, 其右子节点编号为 2*index + 1
(注:图片来自于:http://www.cnblogs.com/Anker/archive/2013/01/23/2873422.html)
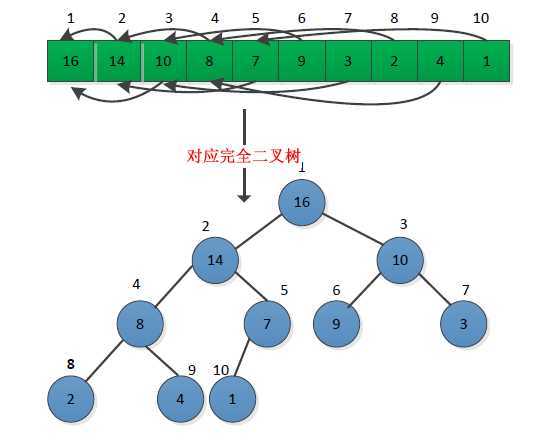
(1) 堆调整
堆调整操作是对编号为index的结点进行“下降”,使以index为根的子树成为最大堆
(注:图片来自于:http://www.cnblogs.com/Anker/archive/2013/01/23/2873422.html)
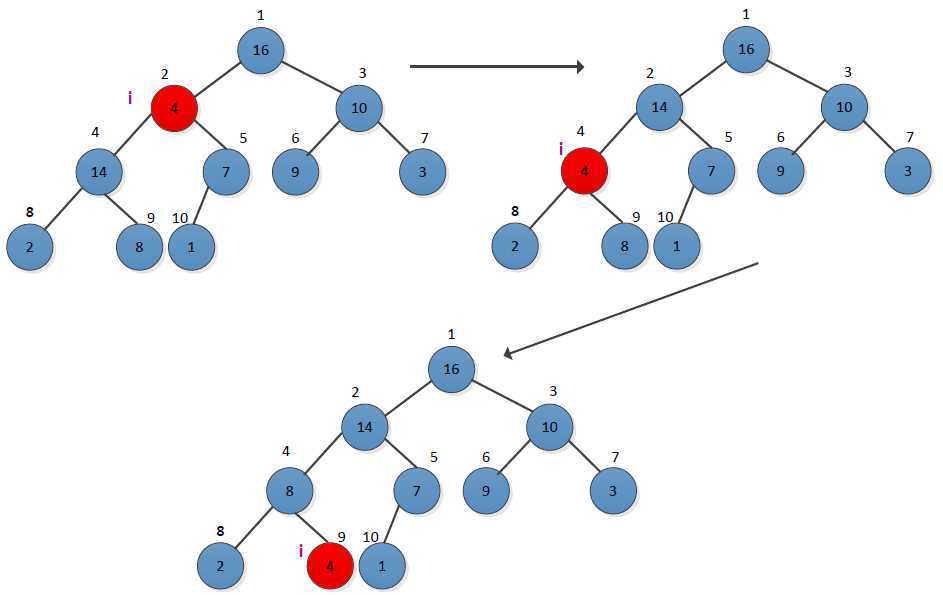
void MaxHeapAdjust(std::vector<int>& num, int index) { int leftIndex = 2 * index; int rightIndex = 2 * index + 1; int largest = 0; if (leftIndex <= num.size()) { if (num.at(leftIndex - 1) > num.at(index - 1)) { largest = leftIndex; } else { largest = index; } } if (rightIndex <= num.size()) { if (num.at(rightIndex - 1) > num.at(largest - 1)) { largest = rightIndex; } } if (largest == 0) return; if (largest != index) { std::swap(num.at(index - 1), num.at(largest - 1)); MaxHeapAdjust(num, largest); } }
(2) 建堆
建立最大堆的过程是自底向上地调用最大堆调整程序将一个数组A[1.....N]变成一个最大堆。将数组视为一颗完全二叉树,从其最后一个非叶子节点(n/2)开始进行堆调整
for (int i = num.size() / 2; i >= 1 ; --i) { MaxHeapAdjust(num, i); }
堆调整和建堆操作都已经说清楚了,再回到本题中来
我们首先取K个数建堆,然后对其后的数字不断与堆顶元素(即最大值)做比较,如果比堆顶元素要小,即更新堆顶元素,并以堆顶元素为根结点进行堆调整操作
void GetKth(const std::vector<int>& num, int kth, std::vector<int>& heap) { if (num.size() == 0 || kth <= 0 || kth > num.size()) { throw std::invalid_argument("invalid_argument"); } for (int i = 0; i < kth; ++i) { heap.push_back(num.at(i)); } for (int i = heap.size() / 2; i >= 1 ; --i) { MaxHeapAdjust(heap, i); } for (int i = kth; i < num.size(); ++i) { if (num.at(i) < heap.at(0)) { heap.at(0) = num.at(i); MaxHeapAdjust(heap, 1); } } }
最后上一张图总结一下两种方法的优缺点:

剑指offer (30) 最小的K个数,布布扣,bubuko.com
标签:style class blog code http color
原文地址:http://www.cnblogs.com/wwwjieo0/p/3807015.html