Computer Science Theory for the Information Age-5: 学习理论——VC维的定义以及一些例子

标签：style   blog   class   code   tar   ext   

学习理论——VC维的定义以及一些例子

    本文主要介绍一些学习理论上的东西。首先，我们得明确，从训练集上学习出来的分类器的最终目标是用于预测未知的样本，那么我们在训练的时候该用多少的样本才能使产生的分类器的效果尽可能的好呢？这些就是VC-理论要解决的问题。在介绍这个理论之前，我们得先介绍一个比较抽象的概念——VC维。这个指标是用与衡量假设空间的复杂程度。为了能更好的理解VC维，本文还会举一些例子来加深理解。

（一）由一个例子引出的动机

    为了更好的说明为什么我们要定义这个VC维，我们先来看一个例子。假设有一个数据库，这个数据库包含每个职员的年纪和工资，那么我们现在要查询35岁到45岁工资为60000～70000的职员数量？为了解决这个查询问题，我们将每个职员用一个二维的点来表示，坐标分别代表年龄和工资，那么这个查询问题就等价于：有多少个点落入一个与坐标轴平行的矩形里面。现在假设这个数据库的数据量非常大，我们不可能统计所有的点，所以我们一般在查询前先固定一个样本，然后统计这个样本里有多少个点落入矩形内，然后用这个样本估计出来的比例代替总体的比例。

    为了达到上述目的，我们总是希望所估计出来的值跟真实的值尽可能的接近。而根据大数定理可知，样本点越多，那么估计的效果就越好。但我们更希望能找样本点大小跟估计的精度之间的关系，也就是说找到最少的样本可以保证：以 $1-\delta$ 的概率使估计的值跟真实值之间的差在 $\epsilon$ 之内，通常这里的的 $\delta$ 和 $\epsilon$ 都很小。现在回过头来看上述的查询问题，我们规定如果一个矩形所包含的样本点一样，那么我们认为这样的矩形是等价的，因为用这些等价的矩形计算出来的估计值都是一样的。那么就有一个问题，那就是对于平面上 $n$ 个点，这样的等价矩形的的个数有多少个？

    首先， $n$ 个点的子集个数为 $2^n$ 个，所以矩形个数不会超过 $2^n$ ，但事实上这样的矩形只有 $\mathcal{O}(n^4)$ 。因为对于每一等价的矩形类都存在一个最小的矩形（将矩形四个边往里缩小直到遇到样本点时停止），而每一个最小矩形都最多只需要四个样本点即可确定，所以 $n$ 个点最多只能确定 $\mathcal{O}(n^4)$ 个最小矩形，也就是说等价矩形类的个数不超过 $\mathcal{O}(n^4)$ 。其实也可以直观的理解上述矩形等价类的个数为什么不是所有的子集数，我们假设这个等价矩形类的个数就是 $2^n$ 个，也就是说矩形内的样本点所行成的子集可以是任何子集。但事实上这是不可能的。举个例子，我们有五个样本点，其中前四个样本点分别处在一个矩形的四个边，而第五个样本点在矩形的内部，那么我们根本没办法形成这样的矩形使其仅包含前四个样本点（任何包含前四个样本点的矩形必定包含第五个样本点），也就是说这个矩形根本就无法形成仅包含前四个样本点的子集。注意这里的4其实就是这个矩形类对应的VC维，而在你了解了后面要介绍的打散概念后，在回过来看这个例子应该会理解的更加深入。

    令 $U$ 所有的职工集合，其大小为 $N$ 。 $\epsilon$ 是给定的容忍系数参数，随机抽取一个样本大小为 $n$ 的样本 $S$ 。对于每一个查询矩形 $R$ ，我们用 $\frac{|R\cap S|}{n}N$ 来估计 $|R\cap U|$ ，也就是说用样本计算出来的值来估计真实的值。我们当然希望对于每一个 $R$ 估计的误差都比较小，即对于所有的 $R$ 有：

$$\left| | R\cap U| - \frac{N}{n}|R\cap S|\right|\leq\epsilon N$$

当然这是不可能的，但我们可以通过选择较大的样本使出现大误差的概率比较小，也就是说我们选择的样本必须使以下不等式成立：

$$\begin{equation}\mathop{Pr}(\left| | R\cap U| - \frac{N}{n}|R\cap S|\right|>\epsilon N\ \text{for some R})\leq\delta\label{equ:1}\end{equation}$$

接下去我们来计算需要多大的样本才能使式子 $\ref{equ:1}$ 成立？

    首先，样本 $S$ 是从 $U$ 中均匀随机选取，那么对于一个固定 $R$ ，我们选到的样本点落入 $R$ 的概率 $q=\frac{|R\cap U|}{N}$ ，所以样本落入 $R$ 的个数（即 $|R\cap S|$ ）服从二项式分布 $B(S,q)$ 。因此根据Chernoff Bounds可知，当 $0\leq\epsilon\leq 1$ 时：

$$\begin{equation}\mathop{Pr}(\left| |R\cap U|-\frac{N}{n}|R\cap S|\right|>\epsilon N)\leq e^{-\frac{\epsilon^2n}{2q}}+e^{-\frac{\epsilon^2n}{3q}}\leq2e^{-\frac{\epsilon^2n}{3}}\end{equation}$$

对于某个固定的 $R$ 有上述的不等式，而对于所有的 $\mathcal{O}(n^4)$ 个 $R$ ，使用联合界得到：

$$\begin{equation}\mathop{Pr}(\left| |R\cap U| - \frac{N}{n}|R\cap S|\right|>\epsilon N\ \text{for some}\ R)\leq Cn^4e^{-\frac{\epsilon^2n}{3}}\end{equation}$$

令 $\delta\geq Cn^4e^{-\frac{\epsilon^2n}{3}}\Longrightarrow n\geq\frac{2}{\epsilon^2}(\mathop{ln}Cn^4+\mathop{ln}\frac{1}{\delta})$ 。所以只要令 $n\geq\frac{2}{\epsilon^2}(\mathop{ln}Cn^4+\mathop{ln}\frac{1}{\delta})$ 即可使上述不等式成立。

    在另外一种更一般的情况，假设我们在平面上有概率分布 $P$ ，也就是说每个点不是以均匀的概率出现，而是以概率分布 $P$ 出现，那么我们该如何估计 $\mathop{Pr}(R)$ ？同样，我们可以根据 $P$ 独立的选取大小为 $n$ 的样本 $S$ ，然后用 $\frac{|S\cap R|}{n}$ 去估计 $\mathop{Pr}(R)$ ，同样我们希望对于每一个 $R$ ，这样的估计都会很好。事实上，这是比前一个例子更一般的情况，在前一个例子中在每一个点出现的概率为 $\frac{1}{N}$ ，而在这个例子中矩形的数量不再是 $\mathcal{O}(n^4)$ ，因为 $P$ 是连续的，也就是说矩形的数量是无限的，所以用联合界来求上界的方法不可取。而VC维对这样的情况或者更一般的情况都会有一个较好的结果，更一般的情况指的是区域不一定是矩形，也可能是半空间、球体等。对于每一类区域，比如矩形、半空间，它都有一个参数叫VC维。对于以下的概率都可以用VC维来界定它的上界：

$$\mathop{Pr}(|\text{实际值}-\text{估计值}|>\epsilon)<\delta$$

这里 $\delta$ 与 $\epsilon$ 和VC维有关。

（二）VC维的定义

定义：一个集合系统记为 $(U,\mathcal{S})$ ，其中 $U$ 为这个集合的全集，可以是有限的也可以是无限的， $\mathcal{S}$ 为 $U$ 的子集所组成的集合。

比如上一节介绍的例子中， $U=\mathbb{R}^2$ ， $\mathcal{S}$ 就是所有平行矩形的集合。

定义：打散概念。一个子集 $A\subseteqq U$ ，如果 $A$ 的每一个子集都可以用 $A$ 与 $\mathcal{S}$ 中的某个元素的相交来表示，那么我们就说集合 $A$ 能够被 $\mathcal{S}$ 打散。

也就是说，对于 $A$ 中的任一子集，都可以用 $A\cap S,S\in\mathcal{S}$ 来表示。

定义：VC维。一个集合系统 $(U,\mathcal{S})$ 的VC维定义为能够被 $\mathcal{S}$ 打散的最大的 $U$ 的子集。

也就是说假设 $(U,\mathcal{S})$ 的VC维为 $d$ 的话，那么肯定存在一个子集 $A\in U,|A|=d$ 能够被 $\mathcal{S}$ 打散，并且对于任意 $B\subseteqq U, |B|>d$ 肯定不可以被 $\mathcal{S}$ 打散。

（三）VC维的例子

 1. 与坐标轴平行的矩形的VC维。

    首先，至少存在四个点的子集可以被平行的矩形打散，比如以下的四个点

并且对任意五个点肯定不会被打散，任画五个点，用一个最小的矩形将这五个点包围起来，则最多只需要4个点即可确定这个矩形，现在如果我们把这四个点形成一个子集，那么不存在矩形仅仅只包含住这四个点。所以与坐标轴平行的矩形的VC维 $d=4$ 。

2. 实数线上的区间。

    很显然，实数线上的区间的VC维 $d=2$ 。

3. 实数线上的一对区间。

    很显然，从上图可知存在四个点可以被打散，对任意的五个点，我们只需要取1，3，5就无法用两个区间去包含住。

4. 凸多边形。

    凸多边形的VC维是无限的。首先，我们在单位圆上选 $n$ 个点，那么这 $n$ 个点的任意子集总可以用凸多边形来包围，而 $n$ 可以趋向无穷大。

5. d维半空间。

定义：半空间： $\{x|\alpha^T x\geq \alpha_0\}$ ，超平面的一边。

首先证明存在 $d+1$ 个点可以被半平面打散。选择原点加上 $d$ 个坐标轴上的单位向量，设 $A$ 是这 $d+1$ 个点的任一个子集。第一种情况， $A$ 包含原点，取 $\alpha$ ，其中 $\alpha$ 的第 $i$ 个分量定义如下： $\alpha_i=1$ 当且仅当第 $i$ 个坐标轴的点不在 $A$ ，否则 $\alpha_i=0$ 。所以对于 $A$ 中任一个元素 $x^T\alpha=0\leq 0$ ，对于不在 $A$ 中的任一个元素 $x^T\alpha=1>0$ ，所以在这种情况下，这 $d+1$ 个顶点也就可被打散。

    第二种情况， $A$ 不包含原点，取 $\alpha$ ，其中 $\alpha$ 的第 $i$ 个分量定义如下： $\alpha_i=1$ 当且进当第 $i$ 个坐标轴的点不在 $A$ ，否则 $\alpha_i=-1$ 。所以对于 $A$ 中任一个元素 $x^T\alpha=-1\leq 0$ ，对于不在 $A$ 中的任一元素 $x^T\alpha=0\ \text{or}\ 1\geq 0$ ，所以这种情况下，这 $d+1$ 个顶点也可被打散。

    现在证明任何一个 $d+2$ 个点形成的子集都不能被打散。

    定义凸壳（Convex Hull）：对于一个集合 $A=\{x_1,x_2,\cdots,x_n\}$ ，由 $A$ 所形成的凸壳记为 $\mathop{convex}(A)=\{x|x=\sum_i\alpha_ix_i,0\leq\alpha_i\leq1,\sum_i\alpha_i=1\}$ 。

直观上看，这个凸壳就是用一个最小的凸区域来包围集合 $A$ 。

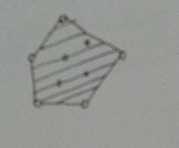
假如一个 $d+2$ 点的集合中存在二个子集 $A$ 和 $B$ ， $A\cap B=\varnothing$ ， $\mathop{convex}(A)\cap\mathop{convex}(B)\neq\varnothing$ 的话，那么我们无法用一个超平面将 $A$ 与 $B$ 分隔开来，也就是说不存在超平面它的一边只包含 $A$ 或 $B$ ，即不存在只包含 $A$ 或 $B$ 的半空间，所以这 $d+2$ 集合无法用半空间打散。

定理（Radon）：对任意集合 $S\in\mathbb{R}^d$ 且满足 $|S|\geq d+2$ ，那么存在 $S$ 的一个划分 $A$ 和 $B$ 使得 $\mathop{convex}(A)\cap\mathop{convex}(B)\neq\varnothing$ 。

证明：不失一般性我们只证明 $|S|=d+2$ 。

    构造矩阵 $\mathbf{A}_{d\times(d+2)}$ ， $\mathbf{A}$ 的每一列都是 $S$ 的一个点，在 $\mathbf{A}$ 的最后一行加上一个全1的行向量得到 $\mathbf{B}=\left(\begin{array}&\mathbf{A}\\\mathbf{1}^T\end{array}\right)$ ，由于 $\mathop{rank}(B)\leq d+1$ ，所以 $\mathbf{B}$ 的列是线性相关的。所以方程 $\mathbf{B}x=0$ 存在非零解 $x=(x_1,x_2,\cdots,x_n)^T$ ，把 $x$ 重新排序，使 $x_1,\cdots,x_s\geq 0, x_{s+1},\cdots,x_{d+2}<0$ 。由于 $\mathbf{B}$ 的最后一行全1，故 $\sum_{i=1}^{d+2}x_i=0$ 。所以肯定同时存在正负分量。

    将 $x$ 进行正则化，即将 $x$ 的每个分量都除以 $\sum_{i=1}^sx_i$ ，得一个新的 $x^\prime$ （ $x^\prime$ 同样是 $\mathbf{B}x=0$ 的解，并且为了方便我仍然记为 $x$ ），故有 $\sum_{i=1}^sx_i=1$ 。记 $b_i$ 为 $\mathbf{B}$ 的第 $i$ 列（相应 $\alpha_i$ 为 $\mathbf{A}$ 的第 $i$ 列）。

    由 $\mathbf{B}x=(b_1,b_2,\cdots,b_s,b_{s+1},\cdots,b_{d+2})x=0$ $\Longrightarrow$ $\sum_{i=1}^{d+2}b_ix_i=0$ $\Longrightarrow$ $\sum_{i=1}^sb_ix_i+\sum_{i=s+1}^{d+2}b_ix_i=0$ $\Longrightarrow$ $\sum_{i=1}^sb_i|x_i|=\sum_{i=s+1}^{d+2}b_i|x_i|$ $\Longrightarrow$ $\sum_{i=1}^s\left(\begin{array}&\alpha_i\\1\end{array}\right)|x_i|=\sum_{i=s+1}^{d+2}\left(\begin{array}&\alpha_i\\1\end{array}\right)|x_i|$ $\Longrightarrow$ $\left\{\begin{array}&\sum_{i=1}^s\alpha_i|x_i|=\sum_{i=s+1}^{d+2}\alpha_i|x_i|\\\sum_{i=1}^s|x_i|=\sum_{i=s+1}^{d+2}|x_i|\end{array}\right.$ 。由 $\sum_ix_i=0\Longrightarrow\sum_{i=1}^s|x_i|=\sum_{i=s+1}^{d+2}|x_i|=1$ 。记集合 $A=(\alpha_1,\cdots,\alpha_s)$ ，集合 $B=(\alpha_{s+1},\cdots,\alpha_{d+2})$ ，则 $\mathop{convex}(A)=\sum_{i=1}^s\alpha_i|x_i|, \mathop{convex}(B)=\sum_{i=s+1}^{d+2}\alpha_i|x_i|$ 。所以， $\mathop{convex}(A)\cap\mathop{convex}(B)\neq\varnothing$ 。注意，这里的 $\mathop{convex}(A)\neq\mathop{convex}(B)$ ， $\sum_{i=1}^s\alpha_i|x_i|=\sum_{i=s+1}^{d+2}\alpha_i|x_i|$ 只表示存在一个系数使二者相等，并不是说对所有系数都相等。

 6. $d$ 维空间的球体。

    一个 $d$ 维空间的球体： $\{x||x-x_0|\leq r\}$ ，它的VC维是 $d+1$ 。首先，存在 $d+1$ 个点可以被半空间打散，那么也肯定存在 $d+1$ 个点可以被 $d$ 维球体打散。现在我们证明任意 $d+2$ 个点都不能被球体打散。

    反证法：假设有一个 $d+2$ 个点的集合 $S$ 可以被球体打散，那么意味着对任何 $A_1\subseteqq S, A_2\subseteqq S, A_1\cap A_2=\varnothing, A_1\cup A_2=S$ ，存在着球体 $B_1,B_2$ 分别只包含 $A_1,A_2$ ，即 $B_1\cap S=A_1,B_2\cap S=A_2$ (尽管 $B_1\cap B_2$ 有可能不为空集，但相交的部分决不含有 $S$ 中的点)。那么可以肯定存在一个超平面，其一边只包含 $A_1$ ，一边只包含 $A_2$ ，即这 $d+2$ 个点可以被半空间打散，这与前面的结论矛盾。

（四）打散函数。

     考虑一个集合系统 $(U,\mathcal{S})$ ，它的VC维为 $d$ ，那么对于 $A\subseteqq U, |A|=n\leq d$ ， $A$ 可以被打散成 $2^n$ 份，也就是说存在 $2^n$ 个 $A$ 的子集，可以用 $S\in\mathcal{S}$ 表示成 $A\cap S$ 。那么对于 $|A| = n >d$ ， $A$ 可以被打散成多少份呢？这就是我们接下去要介绍的打散函数（shatter-function）

定义打散函数：一个集合系统 $(U,\mathcal{S})$ 的打散函数 $\Pi_{\mathcal{S}}(n)$ 指的是大小为 $n$ 的集合 $A\in U$ 中能够用 $A\cap S,S\in\mathcal{S}$ 表示的子集个数。即 $\Pi_{\mathcal{S}}(n)=\max_{A\subseteqq U,|A|=n}|\{A\cap S|S\in \mathcal{S}\}|$ 。

很显然，当 $n\leq d$ 时， $\Pi_{\mathcal{S}}(n)=2^n$ ，也就是说当 $n\leq d$ 时，打散函数以 $2^n$ 增长；当 $n>d$ 时，他的增长将变慢，事实上可以证明 $\Pi_{\mathcal{S}}(n)$ 以 $n$ 的多项式增长。如果VC维是无限的话，那么 $\Pi_{\mathcal{S}}(n)$ 将一直以指数级增长。

    有了 $\Pi_{\mathcal{S}}(n)$ 的定义后，那么VC维也可以定义成 $dim(\mathcal{S})=\max\{n|\Pi_{\mathcal{S}}(n)=2^n\}$ 。在之前我们已经看到对于平行于坐标轴的矩形，最多只有 $\mathcal{O}(n^4)$ 个子集可以用矩形包围住，这里的指数4刚好是平行矩形系统的VC维。

（五）打散函数与VC维的关系。

    首先来证明一个不等式 $\sum_{i=0}^d\binom{n}{i}=\binom{n}{0}+\cdots+\binom{n}{d}\leq2n^d$ 。

采用归纳法证明 $d<n$ 时成立。显然，当 $d=0,1$ 时等式成立；假设 $d=k$ 时 $\sum_{i=0}^k\binom{n}{i}\leq2n^k$ 成立，则

$$\sum_{i=0}^{k+1}\binom{n}{i}=\sum_{i=0}^k\binom{n}{i}+\binom{n}{k+1}\leq2n^k+\frac{n(n-1)\cdots (n-k)}{(k+1)!}\leq2n^k+n^{k+1}\leq 2n^{k+1}$$

所以 $\sum_{i=0}^d\binom{n}{i}\leq2n^d$ 成立。

    当 $d\geq n$ 时， $\sum_{i=0}^d\binom{n}{i}=2^n\leq2n^d$ ，由 $\frac{2n^d}{2^n}=\frac{2n^nn^{d-n}}{2^n}\geq2(\frac{n}{2})^n\geq 1$ 而得到。

    故，综上： $\sum_{i=0}^d\binom{n}{i}\leq2n^d$ 。

 利用上述不等式，我们可以证明如下的定理。

定理：对于一个VC维至多为 $d$ 的任意集合系统 $(U,\mathcal{S})$ ， $\Pi_{\mathcal{S}}(n)\leq \sum_{i=0}^d\binom{n}{i}$ 对所有 $n$ 都成立。

 证明：以下我们分三种情况对上述定理进行证明：

1. 当 $n\leq d$ 时， $\sum_{i=0}^d\binom{n}{i}=2^n$ 且 $\Pi_{\mathcal{S}}(n)=2^n$ ，所以定理上的不等式成立。

2. 当 $d=0$ 时，我们可以证得 $|\mathcal{S}|\leq 1$ 。因为若 $|\mathcal{S}|>1$ ，则 $|\mathcal{S}|$ 中至少有两个集合 $S_1,S_2$ ，并且存在 $x\in S_1$ 且 $x\notin S_2$ ，于是我们可以令 $A=\{x\}$ ，则 $A$ 可以被 $\mathcal{S}$ 打散，即 $(U,\mathcal{S})$ 的VC维大于等于1，这于 $d=0$ 产生矛盾，所以 $|\mathcal{S}|\leq 1$ 。

    若 $|\mathcal{S}|= 1$ ，则 $\Pi_{\mathcal{S}}(n)=1$ 对所有 $n$ 都成立， $\Pi_{\mathcal{S}}(n)=1\leq\binom{n}{0}=1$ 。

    若 $|\mathcal{S}|= 0$ ，则 $\Pi_{\mathcal{S}}(n)=0$ 对所有 $n$ 都成立， $\Pi_{\mathcal{S}}(n)=0\leq\binom{n}{0}=1$ 。

3. 当 $n>d$ 时，令 $A\in U, \Pi_{\mathcal{S}}(n)$ 表示可以表示成 $A\cap S, S\in\mathcal{S}$ 的 $A$ 的子集个数（注意这里的 $A$ 指所有满足 $|A|=n$ ）。不失一般性，令 $U=A$ ，将 $S\in\mathcal{S}$ 用 $S\cap A$ 代替，并且移掉相同的集合(比如 $S_1\cap A=S_2\cap A$ ，则我们只保留其中的一个)，这样处理后 $\Pi_{\mathcal{S}}(n)=|\mathcal{S}|$ ，所以要证 $\Pi_{\mathcal{S}}(n)\leq\sum_{i=0}^d\binom{n}{i}$ ，即证 $|\mathcal{S}|\leq\sum_{i=0}^d\binom{n}{i}$ 。

    构造一个新的集合系统 $(A-\{u\},\{S-\{u\}|S\in\mathcal{S}\})$ ，记为 $(A-\{u\},\mathcal{S}_1)$ 。我们来讨论集合 $S\subseteqq A-\{u\}$ 的情况。

   (1) $S$ 与 $S\cup\{u\}$ 只有一个在 $\mathcal{S}$ 中，则对 $\mathcal{S}$ 与 $\mathcal{S}_1$ 的贡献各一个；(2) $S$ 与 $S\cup\{u\}$ 两个都在 $\mathcal{S}$ 中，则对 $\mathcal{S}$ 的贡献为两个，对 $\mathcal{S}_1$ 的贡献为一个。所以 $|\mathcal{S}|$ 比 $|\mathcal{S}_1|$ 大，并且多出的数量为出现(2)的情况。

    构造一个新的集合系统 $(A-\{u\}, \{S|\text{both}\ S\ \text{and}\ S\cup\{u\}\ \text{are in}\ \mathcal{S}\})$ ，记为 $(A-\{u\},\mathcal{S}_2)$ 。所以 $|\mathcal{S}|=|\mathcal{S}_1|+|\mathcal{S}_2|=\Pi_{\mathcal{S}_1}(n-1)+\Pi_{\mathcal{S}_2}(n-1)=\Pi_{\mathcal{S}}(n)$ 。现在来证明以下两个结论：

(1) $\mathcal{S}_1$ 的VC维至多为 $d$ ;

(2) $\mathcal{S}_2$ 的VC维至多为 $d-1$ 。

对于(1)，假如 $\mathcal{S}_1$ 的VC维超过 $d$ ，那么 $\mathcal{S}$ 的VC维也肯定要超过 $d$ ；对于(2)，假如有集合 $B\subseteqq A-\{u\}, |B|\geq d$ 被 $\mathcal{S}_2$ 打散，那么 $B\cup\{u\}$ 肯定也会被 $\mathcal{S}$ 打散。（这是因为 $B\cup\{u\}$ 的子集包括两种，一种是包含 $u$ 的，一种不包含 $u$ ，不包含 $u$ 的肯定可以表示成 $(B\cup\{u\})\cap S$ ，包含 $u$ 的子集记为 $B^\prime\cup\{u\}$ ，由于 $B^\prime=B\cap S, S\in\mathcal{S}$ ，故 $(B^\prime\cup \{u\})=(B\cup\{u\})\cap(S\cup\{u\})$ ，其中 $S\cup\{u\}\in\mathcal{S}$ ）所以 $\mathcal{S}$ 的VC维至多为 $d+1$ ，与题意矛盾。

    最后，由于 $n\leq d，d=0$ 时不等式成立，所以根据归纳法可知：若 $\Pi_{\mathcal{S}_1}(n-1)\leq\sum_{i=0}^d\binom{n-1}{i}, \Pi_{\mathcal{S}_2}(n-1)\leq\sum_{i=0}^{d-1}(n-1)$ 成立，则：

$$\begin{align*}\Pi_{\mathcal{S}}(n) &=\Pi_{\mathcal{S}_1}(n-1)+\Pi_{\mathcal{S}_2}(n-1)\\&\leq\binom{n-1}{0}+\binom{n-1}{1}+\cdots+\binom{n-1}{d}+\binom{n-1}{0}+\binom{n-1}{1}+\cdots+\binom{n-1}{d-1}\\&\leq\binom{n-1}{0}+[\binom{n-1}{1}+\binom{n-1}{0}]+\cdots+[\binom{n-1}{d}+\binom{n-1}{d-1}]\\&\leq\binom{n}{0}+\binom{n}{1}+\cdots+\binom{n}{d}\end{align*}$$

其中 $\binom{n-1}{d-1}+\binom{n-1}{d}=\binom{n}{d}$ 。

（六）相交的集合系统。

    令 $(U,\mathcal{S}_1)$ 和 $(U,\mathcal{S}_2)$ 为集合 $U$ 下的两个集合系统，定义相交系统 $(U,\mathcal{S}_1\cap\mathcal{S}_2)$ ，其中 $\mathcal{S}_1\cap\mathcal{S}_2=\{A\cap B|A\in\mathcal{S}_1,B\mathcal{S}_2\}$ ，注意这里的交不是将 $\mathcal{S}_1$ 和 $\mathcal{S}_2$ 取交运算，而是对 $\mathcal{S}_1$ 和 $\mathcal{S}_2$ 中的元素取交运算。所以根据定义有 $|\mathcal{S}_1\cap\mathcal{S}_2|\leq|\mathcal{S}_1| |\mathcal{S}_2|$ 。

定理： $\Pi_{\mathcal{S}_1\cap\mathcal{S}_2}(n)\leq\Pi_{\mathcal{S}_1}(n)\Pi_{\mathcal{S}_2}(n)$ 。

证明：对于任何的 $A\subseteqq U$ ，以下不等式成立：

$$\begin{align*}&\left| \{A\cap (S_1\cap S_2)| S_1\in\mathcal{S}_1, S_2\in\mathcal{S}_2\}\right|\\\leq&\left| \{A\cap S_1| S_1\in\mathcal{S}_1\}\right|\cdot\left|\{A\cap S_2|S_2\in\mathcal{S}_2\}\right|\end{align*}$$

即 $\Pi_{\mathcal{S}_1\cap\mathcal{S}_2}(n)\leq\Pi_{\mathcal{S}_1}(n)\Pi_{\mathcal{S}_2}(n)$ 。

 

PS: 本人只粗略的检查了一遍，若有任何错误，还望指出，谢谢！

 

Computer Science Theory for the Information Age-5: 学习理论——VC维的定义以及一些例子,布布扣,bubuko.com

Computer Science Theory for the Information Age-5: 学习理论——VC维的定义以及一些例子

标签：style   blog   class   code   tar   ext   

原文地址：http://www.cnblogs.com/boostable/p/iage_VC_dimension.html