标签:class blog code http tar ext
一、决策树分类算法概述
决策树算法是从数据的属性(或者特征)出发,以属性作为基础,划分不同的类。例如对于如下数据集
(数据集)
其中,第一列和第二列为属性(特征),最后一列为类别标签,1表示是,0表示否。决策树算法的思想是基于属性对数据分类,对于以上的数据我们可以得到以下的决策树模型
(决策树模型)
先是根据第一个属性将一部份数据区分开,再根据第二个属性将剩余的区分开。
实现决策树的算法有很多种,有ID3、C4.5和CART等算法。下面我们介绍ID3算法。
二、ID3算法的概述
ID3算法是由Quinlan首先提出的,该算法是以信息论为基础,以信息熵和信息增益为衡量标准,从而实现对数据的归纳分类。
首先,ID3算法需要解决的问题是如何选择特征作为划分数据集的标准。在ID3算法中,选择信息增益最大的属性作为当前的特征对数据集分类。信息增益的概念将在下面介绍,通过不断的选择特征对数据集不断划分;
其次,ID3算法需要解决的问题是如何判断划分的结束。分为两种情况,第一种为划分出来的类属于同一个类,如上图中的最左端的“非鱼类”,即为数据集中的第5行和第6行数据;最右边的“鱼类”,即为数据集中的第2行和第3行数据。第二种为已经没有属性可供再分了。此时就结束了。
通过迭代的方式,我们就可以得到这样的决策树模型。
(ID3算法基本流程)
三、划分数据的依据
ID3算法是以信息熵和信息增益作为衡量标准的分类算法。
1、信息熵(Entropy)
熵的概念主要是指信息的混乱程度,变量的不确定性越大,熵的值也就越大,熵的公式可以表示为:
2、信息增益(Information gain)
信息增益指的是划分前后熵的变化,可以用下面的公式表示:
其中,

表示样本的属性,
)
是属性

所有的取值集合。
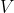
是

的其中一个属性值,

是

中

的值为
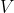
的样例集合。
四、实验仿真
1、数据预处理
我们以下面的数据为例,来实现ID3算法:
摘自 http://blog.sina.com.cn/s/blog_6e85bf420100ohma.html
我们首先需要对数据处理,例如age属性,我们用0表示youth,1表示middle_aged,2表示senior等等。
(将表格数据化)
2、实验结果
(原始的数据)
(划分1)
(划分2)
(划分3)
(最终的决策树)
MATLAB代码
主程序
- %% Decision Tree
- % ID3
-
- %导入数据
- %data = [1,1,1;1,1,1;1,0,0;0,1,0;0,1,0];
-
- data = [0,2,0,0,0;
- 0,2,0,1,0;
- 1,2,0,0,1;
- 2,1,0,0,1;
- 2,0,1,0,1;
- 2,0,1,1,0;
- 1,0,1,1,1;
- 0,1,0,0,0;
- 0,0,1,0,1;
- 2,1,1,0,1;
- 0,1,1,1,1;
- 1,1,0,1,1;
- 1,2,1,0,1;
- 2,1,0,1,0];
-
- % 生成决策树
- createTree(data);
生成决策树
- function [ output_args ] = createTree( data )
- [m,n] = size(data);
- disp(‘original data:‘);
- disp(data);
- classList = data(:,n);
- classOne = 1;%记录第一个类的个数
- for i = 2:m
- if classList(i,:) == classList(1,:)
- classOne = classOne+1;
- end
- end
-
- % 类别全相同
- if classOne == m
- disp(‘final data: ‘);
- disp(data);
- return;
- end
-
- % 特征全部用完
- if n == 1
- disp(‘final data: ‘);
- disp(data);
- return;
- end
-
- bestFeat = chooseBestFeature(data);
- disp([‘bestFeat: ‘, num2str(bestFeat)]);
- featValues = unique(data(:,bestFeat));
- numOfFeatValue = length(featValues);
-
- for i = 1:numOfFeatValue
- createTree(splitData(data, bestFeat, featValues(i,:)));
- disp(‘-------------------------‘);
- end
- end
选择信息增益最大的特征
- %% 选择信息增益最大的特征
- function [ bestFeature ] = chooseBestFeature( data )
- [m,n] = size(data);% 得到数据集的大小
-
- % 统计特征的个数
- numOfFeatures = n-1;%最后一列是类别
- % 原始的熵
- baseEntropy = calEntropy(data);
-
- bestInfoGain = 0;%初始化信息增益
- bestFeature = 0;% 初始化最佳的特征位
-
- % 挑选最佳的特征位
- for j = 1:numOfFeatures
- featureTemp = unique(data(:,j));
- numF = length(featureTemp);%属性的个数
- newEntropy = 0;%划分之后的熵
- for i = 1:numF
- subSet = splitData(data, j, featureTemp(i,:));
- [m_1, n_1] = size(subSet);
- prob = m_1./m;
- newEntropy = newEntropy + prob * calEntropy(subSet);
- end
-
- %计算增益
- infoGain = baseEntropy - newEntropy;
-
- if infoGain > bestInfoGain
- bestInfoGain = infoGain;
- bestFeature = j;
- end
- end
- end
计算熵
- function [ entropy ] = calEntropy( data )
- [m,n] = size(data);
-
- % 得到类别的项
- label = data(:,n);
-
- % 处理完的label
- label_deal = unique(label);
-
- numLabel = length(label_deal);
- prob = zeros(numLabel,2);
-
- % 统计标签
- for i = 1:numLabel
- prob(i,1) = label_deal(i,:);
- for j = 1:m
- if label(j,:) == label_deal(i,:)
- prob(i,2) = prob(i,2)+1;
- end
- end
- end
-
- % 计算熵
- prob(:,2) = prob(:,2)./m;
- entropy = 0;
- for i = 1:numLabel
- entropy = entropy - prob(i,2) * log2(prob(i,2));
- end
- end
划分数据
- function [ subSet ] = splitData( data, axis, value )
- [m,n] = size(data);%得到待划分数据的大小
-
- subSet = data;
- subSet(:,axis) = [];
- k = 0;
- for i = 1:m
- if data(i,axis) ~= value
- subSet(i-k,:) = [];
- k = k+1;
- end
- end
- end
原文链接是:http://blog.csdn.net/google19890102/article/details/28611225
[转载]简单易学的机器学习算法-决策树之ID3算的,布布扣,bubuko.com
[转载]简单易学的机器学习算法-决策树之ID3算的
标签:class blog code http tar ext
原文地址:http://www.cnblogs.com/khunwang/p/3810267.html









