标签:style blog strong http 2014 art
多面体的一个显著特性是可以由有限个向量和标量来描述。在这一节,我们研究多面体的其他有限表示方法,首先是多面体锥和它的极锥。我们将给从两个不同的多面体锥的表示方法,并从极锥的角度证明它们是等价的。
若多面体$C \subseteq \mathbb{R}^n$可表示成如下形式:\begin{align*} C = \{ \boldsymbol{x} \ | \ \boldsymbol{a}_j^\top \boldsymbol{x} \leq 0, j = 1, \dots, r \}, \end{align*}其中$\boldsymbol{a}_j \in \mathbb{R}^n$,$r$是某个正整数,则称$C$为多面体锥(polyhedral cone)。
若锥$C$可表示成如下形式:\begin{align*} C = cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \}) = \{ \boldsymbol{x} \ | \ \boldsymbol{x} = \sum_{j=1}^r \mu_j \boldsymbol{a}_j, \mu_j \geq 0, j = 1, \dots, r \}, \end{align*}其中$\boldsymbol{a}_j \in \mathbb{R}^n$,$r$是某个正整数,则称$C$为有限生成锥(finitely generated cone)。
下面这个引理说明了多面体锥和有限生成锥之间的关系。
命题2.3.1[Farkas‘引理]:设$\boldsymbol{a}_1, \dots, \boldsymbol{a}_r \in \mathbb{R}^n$,那么多面体锥$\{ \boldsymbol{x} | \boldsymbol{a}_j^\top \boldsymbol{x} \leq 0, j = 1, \dots, r \} $和有限生成锥$cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})$都是闭锥且互为极锥。
证明:多面体锥是闭半平面的交集,故多面体锥是闭锥;又有限生成锥可以看作正象限集合$\{ \boldsymbol{\mu} \ | \ \boldsymbol{\mu} \geq 0 \}$在线性变换$\sum_{j=1}^r \mu_j \boldsymbol{a}_j$下的象,于是由命题1.4.20之后的讨论知有限生成锥是闭锥。
由命题2.2.1(1)知\begin{align*} (\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})^* = (cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \}))^*, \end{align*}又由极锥的定义知\begin{align*} (\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})^* = \{ \boldsymbol{x} \ | \ \boldsymbol{a}_j^\top \boldsymbol{x} \leq 0, j = 1, \dots, r \}, \end{align*}于是由上两式可知\begin{align*} (cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \}))^* = \{ \boldsymbol{x} \ | \ \boldsymbol{a}_j^\top \boldsymbol{x} \leq 0, j = 1, \dots, r \}, \end{align*}故多面体锥是有限生成锥的极锥。又易知有限生成锥是闭凸锥,故由命题2.2.1(2)知\begin{align*} ((cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \}))^*)^* = cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \}), \end{align*}于是有\begin{align*} cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \}) = (\{ \boldsymbol{x} \ | \ \boldsymbol{a}_j^\top \boldsymbol{x} \leq 0, j = 1, \dots, r \})^*, \end{align*}故有限生成锥是多面体锥的极锥。
Farkas‘引理还有一个等价的形式,是包含等式约束的。设$\boldsymbol{x}, \boldsymbol{e}_1, \dots, \boldsymbol{e}_m, \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \in \mathbb{R}^n$,则$\boldsymbol{x}$属于多面体锥\begin{align*} P = \{ \boldsymbol{y} \ | \ \boldsymbol{e}_i^\top \boldsymbol{y} = 0, \ \boldsymbol{a}_j^\top \boldsymbol{y} \leq 0, i = 1, \dots, m, j = 1, \dots, r \}, \end{align*}当且仅当$\boldsymbol{x}$可以表示为\begin{align*} \boldsymbol{x} = \sum_{i=1}^m \lambda_i \boldsymbol{e}_i + \sum_{j=1}^r \mu_j \boldsymbol{a}_j, \end{align*}其中$\lambda_i$和$\mu_j$都是标量且$\mu_j \geq 0, j = 1, \dots, r$。证明很简单,设$\boldsymbol{a}_{r+i} = \boldsymbol{e}_i$,$\boldsymbol{a}_{r+m+i} = - \boldsymbol{e}_i$,$i = 1, \dots, m$,于是\begin{align*} P = \{ \boldsymbol{y} \ | \ \boldsymbol{a}_i^\top \boldsymbol{y} \leq 0, i = 1, \dots, r + 2m \}, \end{align*}设$C = cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_{r+2m} \})$,于是由Farkas‘引理知$P^* = C$。
下面这个定理是关于多面体凸性的重要定理,基于该定理,我们可以得到多面体的一个很有用的表示形式。
命题2.3.2[Minkowski-Weyl定理]:一个锥是多面体锥当且仅当它是有限生成锥。
证明:一方面,设有限生成锥是由$\boldsymbol{a}_1, \dots, \boldsymbol{a}_r \in \mathbb{R}^n$生成的。
若$cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \}) = \mathbb{R}^n$,那么锥$cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})$已经是多面体了,故不妨设存在向量$\boldsymbol{b} \not \in cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})$,那么由命题1.5.4的结论(这里满足的是条件(2),锥是闭集,单点集是紧集)知存在一个的超平面严格分离锥$cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})$和向量$\boldsymbol{b}$,即存在向量$\boldsymbol{\xi} \in \mathbb{R}^n$和标量$\gamma \in \mathbb{R}$使得对于$\forall \boldsymbol{x} \in cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})$有$ \boldsymbol{\xi}^\top \boldsymbol{b} > \gamma > \boldsymbol{\xi}^\top \boldsymbol{x}$。由于$cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})$是一个锥,故每一个$\boldsymbol{x}$必须满足$0 \geq \boldsymbol{\xi}^\top \boldsymbol{x}$(否则$\boldsymbol{\xi}^\top \boldsymbol{x}$将无上界),又$0 \in cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})$,故\begin{align*} \boldsymbol{\xi}^\top \boldsymbol{b} > \gamma > 0 \geq \boldsymbol{\xi}^\top \boldsymbol{x}, \ \forall \boldsymbol{x} \in cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \}), \end{align*}这意味着集合\begin{align*} P_b = \{ \boldsymbol{y} \ | \ \boldsymbol{b}^\top \boldsymbol{y} \geq 1, \ \boldsymbol{a}_j^\top \boldsymbol{y} \leq 0, \ j = 1, \dots, r \} \end{align*}非空(至少包含$\boldsymbol{\xi}/\gamma$)。由于$\{\boldsymbol{a}_1, \dots, \boldsymbol{a}_r\}$含有$n$个线性无关的向量,由命题2.1.3中的结论知$P_b$至少有一个极点,记为$\bar{\boldsymbol{y}}$,由命题2.1.4(1)知有两种可能:
事实上,第二种情况是不可能的,因为此时只可能有$\bar{\boldsymbol{y}} = 0$,而这与$\boldsymbol{b}^\top \bar{\boldsymbol{y}} = 1$矛盾,故只可能是第一种情况,这意味着超平面$\{ \boldsymbol{x} \ | \ \bar{\boldsymbol{y}}^\top \boldsymbol{x} = 0 \}$(这是一个$n-1$维的子空间,由$\{\boldsymbol{a}_1, \dots, \boldsymbol{a}_r\}$中$n-1$个线性无关的向量张成)分离锥$cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})$和点$\boldsymbol{b}$且不包含$\boldsymbol{b}$。将$ \boldsymbol{b} $取遍所有不是$cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})$的点,那么可知$cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})$是这$n-1$维超平面对应的半空间(由于这些超平面是由集合$\{\boldsymbol{a}_1, \dots, \boldsymbol{a}_r\}$中的$n-1$个线性无关的向量张成的,故这样的半空间只有有限个)的交集,故锥$cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})$是多面体锥。
若$\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \}$不包含$n$个线性无关的向量,设$\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \}$张成的子空间为$S$,那么有限生成锥\begin{align*} S^\perp + cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \}) \end{align*}含有$n$个线性无关的向量,由前面的推理知该锥是多面体锥。易知\begin{align*} cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \}) = S \cap (S^\perp + cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})), \end{align*}故$cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})$是两个多面体锥的交集,故$cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})$也是多面体锥。
另一方面,考虑多面体锥\begin{align*} C = \{ \boldsymbol{x} \ | \ \boldsymbol{a}_j^\top \boldsymbol{x} \leq 0, j = 1, \dots, r \}, \end{align*}由Farkas‘引理知$C^* = cone(\{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_r \})$,即$C^*$是有限生成锥,由前半部分的证明知$C^*$也是一个多面体锥,故$C^*$可以表示为如下形式:\begin{align*} C^* = \{ \boldsymbol{x} \ | \ \boldsymbol{c}_j^\top \boldsymbol{x} \leq 0, j = 1, \dots, \bar{r} \}, \end{align*}再次由Farkas‘引理和极锥定理知\begin{align*} C = (C^*)^* = cone(\{ \boldsymbol{c}_1, \dots, \boldsymbol{c}_{\bar{r}} \}), \end{align*}故$C$是有限生成锥。
由Minkowski-Weyl定理可以推出:任意多面体均可以表示成有限生成锥和有限点集凸包的和。
命题2.3.3[Minkowski-Weyl表示]:集合$P$是多面体当且仅当存在非空有限点集$\{
\boldsymbol{v}_1, \dots, \boldsymbol{v}_m \}$和有限生成锥$C$使得$P = conv(\{
\boldsymbol{v}_1, \dots, \boldsymbol{v}_m \}) + C$,即\begin{align*} P =
\left\{ \boldsymbol{x} \ | \ \boldsymbol{x} = \sum_{j=1}^m \mu_j
\boldsymbol{v}_j + \boldsymbol{y}, \sum_{j=1}^m \mu_j = 1, \mu_j \geq 0, j
= 1, \dots, m, \boldsymbol{y} \in C \right\}. \end{align*}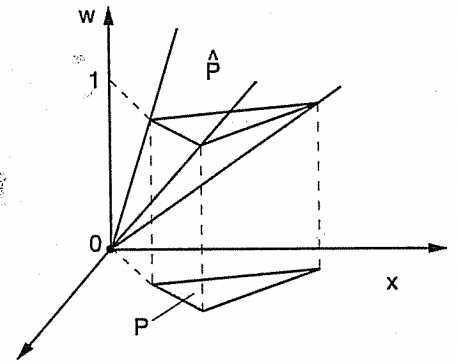
证明:一方面,若$P$是多面体,即\begin{align*}
P = \left\{ \boldsymbol{x} \ | \ \boldsymbol{a}_j^\top \boldsymbol{x} \leq
b_j, j = 1, \dots, r \right\}, \end{align*}其中$\boldsymbol{a}_j \in
\mathbb{R}^n$,$b_j \in \mathbb{R}$,$j = 1, \dots,
r$。如右图所示,考虑$\mathbb{R}^{n+1}$中的多面体锥\begin{align*} \hat{P} = \left\{
(\boldsymbol{x}, w) \ | \ 0 \leq w, \boldsymbol{a}_j^\top \boldsymbol{x}
\leq b_j w, j = 1, \dots, r \right\}. \end{align*}那么有\begin{align*} P =
\left\{ \boldsymbol{x} \ | \ (\boldsymbol{x}, 1) \in \hat{P} \right\},
\end{align*}由Minkowski-Weyl定理知$\hat{P}$也是有限生成锥,故其可表示为
\begin{align*}
\hat{P} = \left\{ (\boldsymbol{x}, w) \ | \ \boldsymbol{x} = \sum_{j=1}^m
\nu_j \bar{\boldsymbol{v}}_j, w = \sum_{j=1}^m \nu_j \bar{d}_j, j = 1,
\dots, m \right\}, \end{align*}其中$\bar{\boldsymbol{v}}_j \in
\mathbb{R}^n$,$\bar{d}_j \in \mathbb{R}$,$j = 1, \dots, m$。由于对于$\forall
(\boldsymbol{x}, w) \in \hat{P}$有$w \geq 0$,故对于$\forall j$有$\bar{d}_j \geq
0$。
设$J^+ = \{ j \ | \ \bar{d}_j > 0 \}$,$J^0 = \{ j \ | \ \bar{d}_j = 0 \}$。对于$j \in J^+$,令$\nu_j \bar{d}_j = \mu_j$,$\bar{\boldsymbol{v}}_j = \bar{d}_j \boldsymbol{v}_j$;对于$j \in J^0$,令$\nu_j \bar{d}_j = \mu_j$,$\bar{\boldsymbol{v}}_j = \boldsymbol{v}_j$,那么$\hat{P}$可重新表示为\begin{align} \label{equ: Minkowski-Weyl 2} \hat{P} = \left\{ (\boldsymbol{x}, w) \ | \ \boldsymbol{x} = \sum_{j \in J^+ \cup J^0} \mu_j \boldsymbol{v}_j, w = \sum_{j \in J^+} \mu_j, \mu_j \geq 0, j \in J^+ \cup J^0 \right\}, \end{align}由于$P = \{ \boldsymbol{x} \ | \ (\boldsymbol{x}, 1) \in \hat{P} \}$,于是\begin{align} \label{equ: Minkowski-Weyl 1} P = \left\{ \boldsymbol{x} \ | \ \boldsymbol{x} = \sum_{j \in J^+ \cup J^0} \mu_j \boldsymbol{v}_j, \sum_{j \in J^+} \mu_j = 1, \mu_j \geq 0, j \in J^+ \cup J^0 \right\}, \end{align}由此可以看出$P$是$conv(\{ \boldsymbol{v}_j \ | \ j \in J^+ \})$和有限生成锥$\{ \sum_{j \in J^0} \mu_j \boldsymbol{v}_j \ | \ \mu_j \geq 0, j \in J^0 \}$的向量和。
另一方面,若$P$是有如式(\ref{equ: Minkowski-Weyl 1})所示的形式,那么$P$可以表示成$P = \{ \boldsymbol{x} \ | \ (\boldsymbol{x}, 1) \in \hat{P} \}$,其中$\hat{P}$是式(\ref{equ: Minkowski-Weyl 2})所示的有限生成锥,由Minkowski-Weyl定理知$\hat{P}$也是多面体,那么由$P = \{ \boldsymbol{x} \ | \ (\boldsymbol{x}, 1) \in \hat{P} \}$可知$P$也是多面体。
根据Minkowski-Weyl表示,我们可以得到多面体的一些代数运算法则。
命题2.3.4[多面体的代数运算法则]:
证明:
多面体可以用来定义多面体函数,具体来说,若函数$f: \mathbb{R}^n \mapsto (-\infty, \infty]$的上境图$epi(f)$为$\mathbb{R}^{n+1}$里的多面体,则称$f$为多面体函数(polyhedral functions)。由于多面体是闭凸集,故多面体函数是闭凸函数。又多面体非空,且$f$不取$-\infty$,故$f$是正常函数。综上,多面体函数是正常闭凸函数。下面这个命题给出了多面体函数的一个表示。
命题2.3.5:设$f: \mathbb{R}^n \mapsto (-\infty, \infty]$是凸函数。那么$f$是多面体函数当且仅当$dom(f)$是多面体且\begin{align} \label{equ: polyhedral functions} f(\boldsymbol{x}) = \max_{j = 1, \dots, m} \{ \boldsymbol{a}_j^\top \boldsymbol{x} + b_j \}, \ \forall \boldsymbol{x} \in dom(f), \end{align} 其中$\boldsymbol{a}_j \in \mathbb{R}^n$,$b_j \in \mathbb{R}$,$m$是某正整数。
证明:一方面,若$f$有式(\ref{equ: polyhedral functions})的形式,则其上境图$epi(f)$可表示为\begin{align*} epi(f) = \left\{ (\boldsymbol{x}, w) \ | \ \boldsymbol{x} \in dom(f) \right\} \cap \left\{ (\boldsymbol{x}, w) \ | \ \boldsymbol{a}_j^\top \boldsymbol{x} + b_j \leq w \right\}, \end{align*}即$epi(f)$可以表示成两个多面体的交集,故$epi(f)$是多面体,即$f$是多面体函数。
另一方面,若$f$是多面体函数,则其上境图$epi(f)$是多面体,可表示为\begin{align} \label{equ: polyhedral functions epi} \left\{ (\boldsymbol{x}, w) \ | \ \boldsymbol{a}_j^\top \boldsymbol{x} + b_j \leq c_j w, j = 1, \dots, r \right\}, \end{align}其中$\boldsymbol{a}_j \in \mathbb{R}^n$,$b_j$和$c_j$是某个标量。由于对于任意$(\boldsymbol{x}, w) \in epi(f)$有$(\boldsymbol{x}, w + \gamma) \in epi(f)$,其中$\gamma$是非负实数,故$c_j \geq 0$(否则$c_j w$无下界)。对式(\ref{equ: polyhedral functions epi})进行归一化,则只可能有两种情况:$c_j = 0$或者$c_j = 1$。若对$\forall j$都有$c_j = 0$,则$f$不是正常函数,这与$f$是多面体函数矛盾。故存在某个$1 \leq m \leq r$的$m$使得\begin{align*} c_j = \begin{cases} 1 & j = 1, \dots, m, \\ 0 & j = m+1, \dots, r, \end{cases}\end{align*}那么\begin{align*} epi(f) = \left\{ (\boldsymbol{x}, w) \ | \ \boldsymbol{a}_j^\top \boldsymbol{x} + b_j \leq w, j = 1, \dots, m, \boldsymbol{a}_j^\top \boldsymbol{x} + b_j \leq 0, j = m+1, \dots, r \right\}, \end{align*}由此可知\begin{align*} dom(f) = \left\{ \boldsymbol{x} \ | \ \boldsymbol{a}_j^\top \boldsymbol{x} + b_j \leq 0, j = m+1, \dots, r \right\}, \end{align*}且\begin{align*} f = \max_{j = 1, \dots, m} \{ \boldsymbol{a}_j^\top \boldsymbol{x} + b_j \}, \ \forall \boldsymbol{x} \in dom(f). \end{align*}
下面两个命题说明多面体函数在加和和线性变换下仍然是多面体函数。
命题2.3.6:若$f_1$和$f_2$是多面体函数且$dom(f_1) \cap dom(f_2) \neq \emptyset$,则$f_1 + f_2$也是多面体函数。
证明:由命题2.3.5知$dom(f_1)$和$dom(f_2)$都是多面体,由命题2.3.4(1)知$dom(f_1) \cap dom(f_2)$也是多面体。再根据命题2.3.5可设\begin{align*} f_1(\boldsymbol{x}) = \max_{j = 1, \dots, m} \{ \boldsymbol{a}_j^\top \boldsymbol{x} + b_j \}, \ \forall \boldsymbol{x} \in dom(f_1), \\ f_2(\boldsymbol{x}) = \max_{j = 1, \dots, \bar{m}} \{ \bar{\boldsymbol{a}}_j^\top \boldsymbol{x} + \bar{b}_j \}, \ \forall \boldsymbol{x} \in dom(f_2), \end{align*}那么对于$\forall \boldsymbol{x} \in dom(f_1) \cap dom(f_2)$有\begin{align*} f_1(\boldsymbol{x}) + f_2(\boldsymbol{x}) & = \max_{j = 1, \dots, m} \{ \boldsymbol{a}_j^\top \boldsymbol{x} + b_j \} + \max_{j = 1, \dots, \bar{m}} \{ \bar{\boldsymbol{a}}_j^\top \boldsymbol{x} + \bar{b}_j \} \\ & = \max_{1 \leq i \leq m, 1 \leq j \leq \bar{m}} \{ \boldsymbol{a}_i^\top \boldsymbol{x} + b_i + \bar{\boldsymbol{a}}_j^\top \boldsymbol{x} + \bar{b}_j \} \\ & = \max_{1 \leq i \leq m, 1 \leq j \leq \bar{m}} \{ (\boldsymbol{a}_i + \bar{\boldsymbol{a}}_j)^\top \boldsymbol{x} + b_i + \bar{b}_j \}, \end{align*}由命题2.3.5知$f_1 + f_2$是多面体函数。
命题2.3.7:设$\boldsymbol{A}$是矩阵,$g$是多面体函数且$dom(g)$至少包含$\boldsymbol{A}\boldsymbol{x}$的一个点,那么$f(\boldsymbol{x}) = g(\boldsymbol{A} \boldsymbol{x})$也是多面体函数。
证明:设$g: \mathbb{R}^n \mapsto (-\infty, \infty]$是多面体函数,由命题2.3.5知$dom(g)$是$\mathbb{R}^n$中的多面体且\begin{align*} g(\boldsymbol{y}) = \max_{j = 1, \dots, m} \left\{ \boldsymbol{a}_j^\top \boldsymbol{y} + b_j \right\}, \ \forall \boldsymbol{y} \in dom(g), \end{align*}其中$\boldsymbol{a}_j \in \mathbb{R}^n$,$b_j \in \mathbb{R}$,$m$是某正整数。又\begin{align*} dom(f) = \left\{ \boldsymbol{x} \ | \ f(\boldsymbol{x}) < \infty \right\} = \left\{ \boldsymbol{x} \ | \ g(\boldsymbol{A}\boldsymbol{x}) < \infty \right\} = \left\{ \boldsymbol{x} \ | \ \boldsymbol{A}\boldsymbol{x} \in dom(g) \right\}, \end{align*}因此$dom(f)$是$dom(g)$在线性变换$\boldsymbol{A}$下的原象,由于$dom(g)$至少包含$\boldsymbol{A}\boldsymbol{x}$的一个点,故$dom(f)$非空,且由命题2.3.4(5)知$dom(f)$也是多面体。于是,对于$\forall \boldsymbol{x} \in dom(f)$有\begin{align*} f(\boldsymbol{x}) & = g(\boldsymbol{A}\boldsymbol{x}) \\ & = \max_{j = 1, \dots, m} \{ \boldsymbol{a}_j^\top \boldsymbol{A} \boldsymbol{x} + b_j \}, \\ & = \max_{j = 1, \dots, m} \{ (\boldsymbol{A}^\top\boldsymbol{a}_j)^\top \boldsymbol{x} + b_j \},\end{align*}由命题2.3.5知$f$也是多面体函数。
标签:style blog strong http 2014 art
原文地址:http://www.cnblogs.com/murongxixi/p/3704506.html