多面体与优化

标签：style   blog   class   ext   color   width   

　　多面体和优化有很大的关系，很多实际问题都可以形式化成和多面体或多面体函数相关的问题。此外，若一个问题的约束是多面体，则往往可以设计出比一般凸约束问题解法更好的优化算法，之前我们已经碰到过一些：

1. 凹函数 $f$ 若在凸集 $C$ 上不是常数函数，那么只可能在 $C$ 的相对边界上取得最小值(命题1.3.4)。
2. 线性函数或凸二次函数 $f$ 在多面体 $C$ 上有下界，那么 $f$ 可在 $C$ 上取得最小值(命题1.4.19)。

　　这一节我们更深入地介绍多面体在优化里的应用，尤其是线性规划(线性函数在多面体上的最小化问题)。线性规划里有一个经典结果：若多面体 $C$ 至少有一个极点且线性函数 $f$ 在 $C$ 上可取得最小值，那么该最小值必然可在 $C$ 的某些极点上取到(当然也可以在非极点上取到)。事实上，这是下面这个命题的特例，这里 $f$ 是凹函数， $C$ 是闭凸集。

　　命题2.4.1：集合 $C$ 是 $\mathbb{R}^n$ 的闭凸子集且至少有一个极点，若凹函数 $f: C \mapsto \mathbb{R}$ 在 $C$ 上可取得最小值，那么该最小值必然可在 $C$ 的某些极点上取到。

　　证明：设 $\boldsymbol{x}^* \in C$ 且 $f$ 在 $\boldsymbol{x}^*$ 处取得最小值。若 $\boldsymbol{x}^* \in ri(C)$ ，由命题1.3.4知 $f$ 是 $C$ 上的常数函数，那么显然 $f$ 可在 $C$ 的某些极点上取到最小值。若 $\boldsymbol{x}^* \not \in ri(C)$ ，由命题1.5.6的结论知存在超平面 $H_1$ 正常分离 $\boldsymbol{x}^*$ 和 $C$ 。由于 $\boldsymbol{x}^* \in C$ ，故 $H_1$ 包含 $\boldsymbol{x}^*$ ，于是 $H_1$ 不包含 $C$ ，那么集合 $C \cap H_1$ 的维度比 $C$ 小。

　　若 $\boldsymbol{x}^* \in ri(C \cap H_1)$ ，那么 $f$ 是 $C \cap H_1$ 上的常数函数，那么 $f$ 在 $C \cap H_1$ 的某些极点上取到最小值(由于 $C$ 有极点，由命题2.1.2知 $C$ 不包含直线，那么 $C \cap H_1$ 也不会包含直线，再由命题2.1.2知 $C \cap H_1$ 至少有一个极点)，又由命题2.1.1知这些极点也是 $C$ 的极点，也即 $f$ 可在 $C$ 的某些极点上取到最小值。若 $\boldsymbol{x}^* \not \in ri(C \cap H_1)$ ，则存在超平面 $H_2$ 正常分离 $\boldsymbol{x}^*$ 和 $C \cap H_1$ ，那么集合 $C \cap H_1 \cap H_2$ 的维度比 $C \cap H_1$ 小。

　　若 $\boldsymbol{x}^* \in ri(C \cap H_1 \cap H_2)$ ，那么 $f$ 是 $C \cap H_1 \cap H_2$ 上的常数函数，如此不断下去(由于每引进一个超平面都会使得集合 $C \cap H_1 \cap \dots$ 的维度降低，最多引进 $n$ 个超平面该过程就会停止，最终集合变成单点集)，直到 $\boldsymbol{x}^*$ 是某个集合 $C \cap H_1 \cap \dots \cap H_k$ 的相对内部点，那么 $f$ 是 $C \cap H_1 \cap \dots \cap H_k$ 上的常数函数，故此时 $f$ 即在 $C \cap H_1 \cap \dots \cap H_k$ 的极点上取得了最小值，再不断地利用命题2.1.1的结论可知这些极点也是 $C$ 的极点，也即 $f$ 可在 $C$ 的某些极点上取到最小值。

　　命题2.4.2[线性规划基本定理]：若多面体 $P$ 至少有一个极点，则在 $P$ 上有下界的线性函数 $f$ 必然可在 $P$ 的某些极点上取到最小值。

　　证明：由于 $f$ 在 $P$ 上有下界，那么由命题1.4.19知 $f$ 在 $P$ 上可取得最小值，由命题2.4.1知结论成立。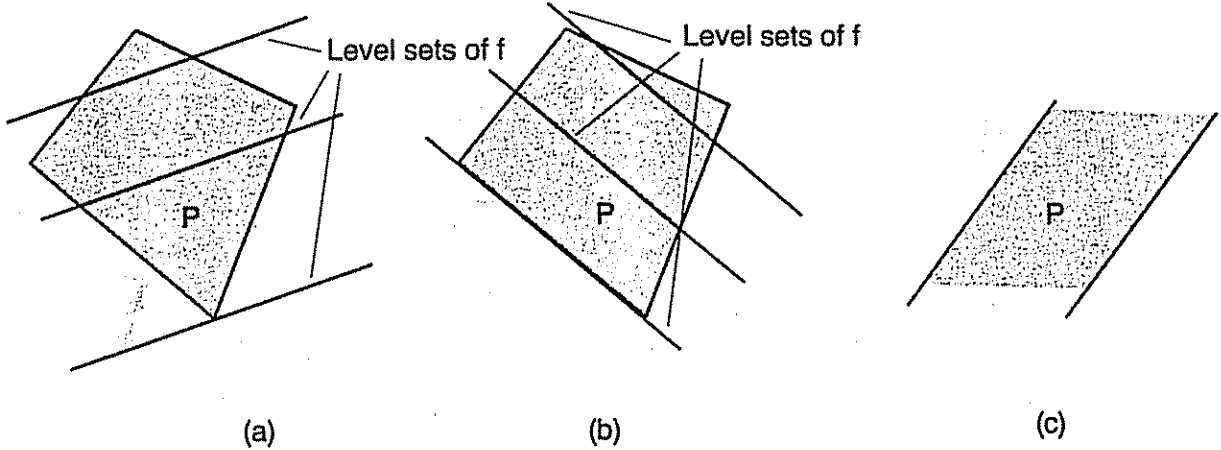

　　上图展示了线性规划的两种可能：

1. 约束集合 $P$ 有极点，那么此时目标线性函数要么在 $P$ 上无下界，要么在 $P$ 的极点上取得最小值。例如设 $P = [0, \infty)$ ，那么目标线性函数 $1 \cdot \boldsymbol{x}$ 在 $P$ 的极点 $0$ 处取得最小值；目标线性函数 $0 \cdot \boldsymbol{x}$ 在 $P$ 的任意一点处都取得最小值；目标线性函数 $-1 \cdot \boldsymbol{x}$ 在 $P$ 上无下界，故在 $P$ 上无法取得最小值。
2. 约束集合 $P$ 没有极点，那么由命题2.1.2知 $P$ 包含直线，那么 $P$ 的回收锥的线性空间 $L_P$ 的维度大于 $0$ ，若目标线性函数在 $P$ 有下界，那么由命题1.4.19知 $f$ 在 $P$ 上取得最小值。又 $f$ 在 $L_P$ 的所有方向上都必须是常数函数(否则 $f$ 无界)，故取得最小值的点集是线性空间为 $L_P$ 的一个多面体，故取得最小值的点集是无界的。例如设 $P = \mathbb{R}$ ，那么目标线性函数 $1 \cdot \boldsymbol{x}$ 在 $P$ 上无下界，故在 $P$ 上无法取得最小值；目标线性函数 $0 \cdot \boldsymbol{x}$ 在 $P$ 上取得最小值的点集就是 $P$ 。

多面体与优化,布布扣,bubuko.com

多面体与优化

标签：style   blog   class   ext   color   width   

原文地址：http://www.cnblogs.com/murongxixi/p/3704688.html