实际上我们真正买过房子的都知道,在选择房子的时候,需要考虑的不仅仅是面积,地段、结构、房龄、邻里关系之类的都应该是考虑对象,所以前面几讲谈论的,单纯用面积来谈房价,不免失之偏颇。
我们加入一些特性来考虑房价问题:
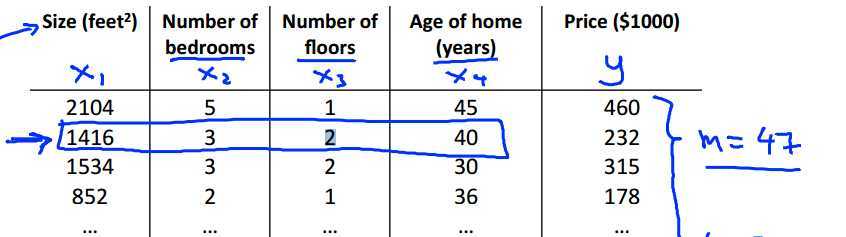
$n$:特性数目
$x ^{(i)}$:输入的第$i$个训练数据
$x ^{(i)} _j$:第$i$个训练数据的第$j$个特性
相应的,$h _\theta (x)$也就变了:
$h _\theta (x) = \theta _0 + \theta _1 x _1 + \theta _2 x _2 + \cdots +\theta _n x _n$
结合上节的向量内容,加上$x _0 = 1$,可得到:
$$ \matrix{x}= \begin{bmatrix} x _0 \cr x _1 \cr \vdots \cr x _n \cr \end{bmatrix} \matrix{\theta}= \begin{bmatrix} \theta _0 \cr \theta _1 \cr \vdots \cr \theta _n \cr \end{bmatrix} $$
$h _\theta (x) = \matrix{\theta} ^T \matrix{x}$
其中,$x _0 = 1$
$J(\matrix{\theta})=J(\theta _0,\theta _1,\cdots,\theta _n)=\frac{1}{2m}\sum _{i=1}^m{(h _\theta(x^{(i)}) - y^{(i)})^2}$
如上一讲所述,重复下面的公式直至收敛:
$\theta _j = \theta _j -\alpha \frac{\partial}{\partial \theta _j}J(\theta _0,\theta _1,\cdots,\theta _n)$
把微分方程计算开,即:
$\theta _j = \theta _j -\alpha \frac{1}{m}\sum _{i=1}^m{(h _\theta(x^{(i)}) - y^{(i)}) x ^{(i)} _j}$
在实际运作中,难免会遇到特征值很大的情况,比如说1~10000000,这时候如果想要处理的话,计算量很大,不是很利于实际操作,所以缩小下范围是个不错的选择。
归一化,其实就是把数据处理下,限制在某一特定范围,便于后续处理,且能加快程序收敛速度。
$x _i=\frac {x _i - \bar{x}} {\sigma}$
$\sigma=\sqrt{\frac {1} {n} \sum _{i=1} ^n {(x _i -\bar{x}) ^2}}$
步长的选择,单变量、多变量并没有什么区别,不能过大,不能过小,至于原因,可以看上一讲的东西,其实都一样。
如果说房子给出了长、宽两项来预测房价,我们都知道的,两变量处理起来比单变量麻烦,其实这时候完全可以用面积来代替长、宽,这样只有一个变量,处理起来也方便很多。
可能有时候线性回归不能很好拟合给定的样本,比如说房价预测:
$h _\theta (x) = \theta _0 +\theta _1(size) +\theta _2{(size)} ^2 +\theta _3 {(size)} ^3$
可能这种式子能更好拟合样本,这时候看式子里有平方、立方,不是线性的了。
其实可以转变成线性的:
$x _1=(size)$
$x _2={(size)} ^2$
$x _3={(size)} ^3$
这样替换进去又是我们熟悉的多变量回归了。
同样开根号也是可以根据实际情况去选择的,处理的时候同上述方法。
除了迭代法之外,其实利用线性代数只是,是可以直接算出$\matrix{\theta}$的。
举个例子,4组特性的房价预测:
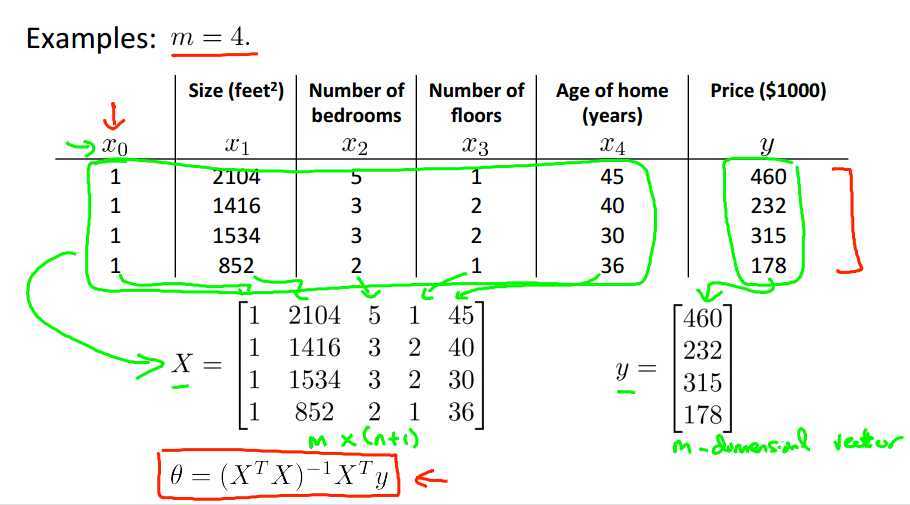
$\theta = (\matrix{X} ^T \matrix{X})^{-1}\matrix{X} ^T \matrix{y}$
$\matrix{X} ^T \matrix{X}$不可逆处理方式:
去掉冗余特性;
删除过多特征。
本篇主要参考了以下资料:
Coursera公开课机器学习:Linear Regression with multiple variables,布布扣,bubuko.com
Coursera公开课机器学习:Linear Regression with multiple variables
原文地址:http://www.cnblogs.com/newc/p/3812982.html