标签:
本文研究如何在区域内随机均匀布点, 来源于 <算法可视化 Visualizing Algorithms>, 这在CAE, 图形学中都有重要意义.
http://www.bilibili.com/video/av2182749/
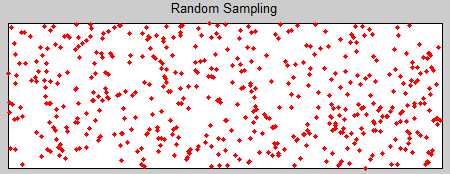
比如在 3*1 的区域内随机布点 1000 个, 如果每个点都是坐标都是随机给的, 结果可能并不均匀.
如 randomPoints.m 所演示的.

1 function randomPoints() 2 xmax = 3; 3 ymax = 1; 4 N = 500; 5 x = xmax*rand(N,1); 6 y = ymax*rand(N,1); 7 figure(1); 8 plot(x,y,‘.‘,‘markerSize‘,5,‘markerEdgeColor‘,‘r‘); hold on; 9 title(‘Random Sampling‘); 10 axis equal; 11 axis([0,xmax,0,ymax]); 12 set(gca,‘xTick‘,[],‘yTick‘,[]); 13 end
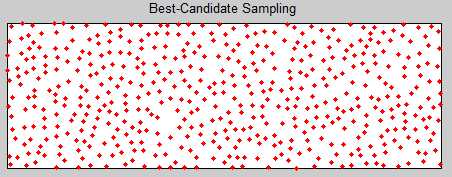
接下来介绍一种方法称为 Best-Candidate Sampling, 基本思路是, 没加一个点需要在若干 (numCandidates) 点 (比如 10)中寻找和已知点最近距离最大的那个点.
每加一个点的伪代码如下:
bestCandidate= 0; bestDistance = 0; loop i=1:numCandidates{ c = [rand(),rand()]; % 随机点 c 的坐标 d = distance( findClosest(samples,c), c ); % 获取 c 和已知点中最近的距离 if (d > bestDistance){ % 如果 c 点的距离大于任何点 bestDistance = d; % 更新最大距离 bestCandidate = c; % 更新最佳点 } }
这种方法可以获得比较均匀的分布, 但是当数据点比较多时, 需要很多的计算量. 另外, numCandidates 越大, 分布也越均匀. 但是同样带来的计算量增长也是不可忽略的. 计算结果可以参考代码 bestCandidate.m

1 function bestCandidate() 2 xmax = 3; 3 ymax = 1; 4 N = 500; 5 x = zeros(N,1); y = zeros(N,1); 6 x(1) = rand(1,1)*xmax; % 初始布置一个点 7 y(1) = rand(1,1)*ymax; % 或许可以布置多个点在边界上哦 8 numCandidates = 10; 9 for ii = 2:N 10 xCand = rand(numCandidates,1)*xmax; % 随机选择 numCand.. 个候选点 11 yCand = rand(numCandidates,1)*ymax; 12 bestDistance = 0; 13 for jj = 1:numCandidates 14 dists = sqrt( (x(1:ii-1)-xCand(jj)).^2 + (y(1:ii-1)-yCand(jj)).^2 ); % 已知点和 jj 号候选点的距离 15 dist = min(dists); % 获取最小的距离 16 if (dist > bestDistance) % 如果 c 点的距离大于任何点 17 bestDistance = dist; % 更新最大距离 18 bestCandidate = jj; % 更新最佳点 19 end 20 end 21 x(ii) = xCand(bestCandidate); y(ii) = yCand(bestCandidate); % 插入一个点 22 end 23 figure(1); 24 plot(x,y,‘.‘,‘markerSize‘,5,‘markerEdgeColor‘,‘r‘); hold on; 25 title(‘Best-Candidate Sampling‘); 26 axis equal; 27 axis([0,xmax,0,ymax]); 28 set(gca,‘xTick‘,[],‘yTick‘,[]); 29 end
结果如下:
最后介绍的方法称为 泊松碟采样 Poisson Disk Sampling, 06~07 年提出. 这种方法效果更佳, 因为它排除了两个点半径小于固定值 r 的情况. 基本思路如下:
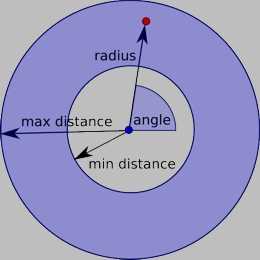
1. 设定随机初始点和背景网格. 为保证每个网格内至多只有一个点, 网格尺寸为 r/2pi, r 为任意两点间的最小距离.
2. 循环直到没有可选点
a) 从已知可选点中选择一个, 在其外生成一个圆环 (内径 r, 外径 2r)
b) 从圆环中选择候选点(典型地, k=30个). 检测候选点和已知点之间的最小距离(可以利用背景网格减少计算量) 假如距离小于设定值 r, 则放弃该候选点; 否则加入一个新点.
c) 假如无法增加候选点, 那么可以将中心点变为不可选.
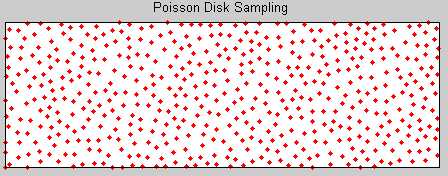
Poisson Disk 方法有很多改进和扩展, 其计算量已经为 O(N lg N), 甚至有快速算法到了 O(N); 但这里为了代码演示, 我们不考虑优化, 也不采用背景网格. 如 poissonDisk.m 所演示的.

1 function poissonDisk() 2 close all;clear all;clc; 3 xmax = 3; 4 ymax = 1; 5 N = 5000; % 一个比较大的数, 足以存放点 6 r = sqrt(3*1/500/pi*2); % 最小半径, 这样设计大约有 500 个点 7 x = zeros(N,1); y = zeros(N,1); 8 ava = zeros(N,1); 9 x(1) = rand(1,1)*xmax; % 初始布置一个点 10 y(1) = rand(1,1)*ymax; % 或许可以布置多个点在边界上哦 11 ava(1) = 1; cnt = 1; 12 numCandidates = 30; 13 while(sum(ava)~=0) % 可选点判断 14 cava = find(ava(1:cnt)); % 找出可选点 15 cnum = cava( floor( rand()*length(cava)+1 )); % 从可选点中选一个 16 rCand = ( rand(numCandidates,1)+1 )*r; % 随机选择 numCand.. 个候选点 17 thetaCand = rand(numCandidates,1)*2*pi; 18 xCand = rCand.*cos(thetaCand) + x(cnum); 19 yCand = rCand.*sin(thetaCand) + y(cnum); 20 % 寻找是否有合适点 21 flag = 0; 22 for jj = 1:numCandidates 23 dists = sqrt( (x(1:cnt)-xCand(jj)).^2 + (y(1:cnt)-yCand(jj)).^2 ); % 已知点和 jj 号候选点的距离 24 dist = min(dists); % 获取最小的距离 25 if (dist > r && xCand(jj) <= xmax && yCand(jj) <= ymax ... 26 && xCand(jj) >= 0 && yCand(jj) >= 0 ) % 如果 c 点的距离大于任何点 27 x(cnt+1) = xCand(jj); y(cnt+1) = yCand(jj); 28 ava(cnt+1) = 1; 29 cnt = cnt + 1; 30 flag = 1; 31 break; 32 end 33 end 34 % 以下代码能运行表示在 numCandidates 候选点中没有可用的, 故将点 cnum 变为不可选 35 if flag == 0 36 ava(cnum) = 0; 37 end 38 end 39 figure(1); 40 plot(x,y,‘.‘,‘markerSize‘,5,‘markerEdgeColor‘,‘r‘); hold on; 41 title(‘Poisson Disk Sampling‘); 42 axis equal; 43 axis([0,xmax,0,ymax]); 44 set(gca,‘xTick‘,[],‘yTick‘,[]); 45 end
扩展阅读:
Jittered Grid: 将区域划分成一个个方块, 然后在方块里任意填充点. 同样效果不太好.
http://devmag.org.za/2009/05/03/poisson-disk-sampling/
标签:
原文地址:http://www.cnblogs.com/willowfly/p/4557643.html