标签:
A problem is a set of numbers in computability theory.
Problem $A$ is said to be m-reducible to problem $B$ ($A\leq_m B$) iff there exists a total computable function $f$ such that $x\in A\Leftrightarrow f(x)\in B$. This is the so-called m-reduction.
Given $A\leq_m B$, we have known that:
(i) if $B$ is recursive, then $A$ must be recursive;
(ii) if $B$ is r.e., then $A$ must be r.e.;
(iii) if $A$ is productive, then $B$ must be productive;
(iv) if $A$ is creative and $B$ is r.e., then $B$ must be creative.
Problem $A$ is r.e. iff $A\leq_m K$. An r.e. set is m-complete if every r.e. set is m-reducible to it. Thus, $K$ is one of m-complete sets.
(Myhill‘s Theorem) A set is m-complete iff it is creative.
Two sets $A$ and $B$ are many-one equivalent ($A\equiv_m B$) iff both $A\leq_m B$ and $B\leq_m A$ hold. Many-one equivalence is an equivalence relation since it is reflexive, symmetric and transitive. We define the equivalence class of a problem $A$ based on $\equiv_m$ as $d_m(A)=\{B |\text{ }A\equiv_m B\}$, which is known as m-degree.
Given two m-degrees $\mathbf{a}$ and $\mathbf{b}$, we further define $\mathbf{a}\leq_m\mathbf{b}$ iff $(\exists A_1\in \mathbf{a})(\exists B_1\in\mathbf{b})(A_1\leq_m B_1) $ and $(\forall A_2\in\mathbf{a})(\forall B_2\in\mathbf{b})(B_2\nleqslant_m A_2) $. This is a partial order on m-degrees since it is transitive and irreflexive.
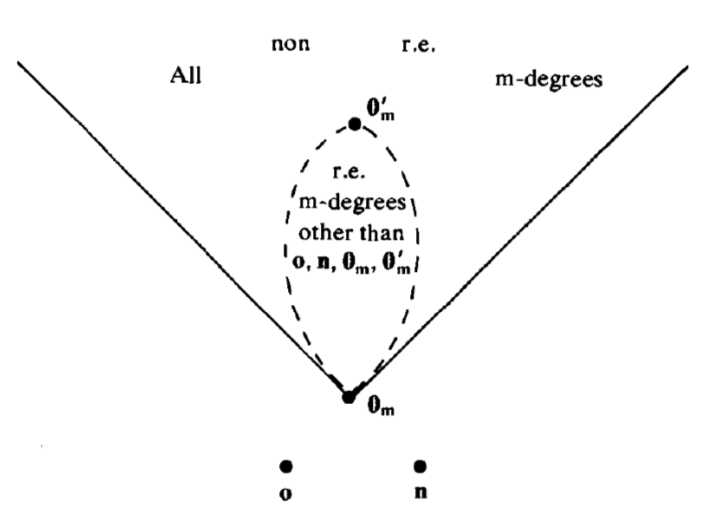
In the picture above, $o=\{\varnothing\}$, $n=\{\mathbb{N}\}$, $\mathbf{0}_m=\{A|A\text{ is recursive}\}$, and $\mathbf{0}_m‘=d_m(K)$. All m-degrees form a join-semilattice since for any $\mathbf{a}$ and $\mathbf{b}$, if we pick $A\in\mathbf{a}$ and $B\in\mathbf{b}$, there will exist $d_m(A\oplus B)$ as the least upper bound of $\mathbf{a}$ and $\mathbf{b}$. About lattice, we give the following picture as a refresher.
A function $f$ is polynomial-time computed by a program $P$ iff there exists some constants $c$ and $k$ such that for any instance $n$, $f(n)$ is computed by $P(n)$ within $c\cdot n^k$ steps.
A problem is polynomial-time decidable iff it is polynomial-time partially decidable.
A problem $A$ is poly-reducible to another problem $B$ ($A\leq_P B$) iff there exists a polynomial-time total computable function $f$ such that $A(n)\Leftrightarrow B(f(n))$.
A decision problem is a P problem iff there is a polynomial-time algorithm to solve it.
A decision problem belongs to NP iff there is a polynomial-time certifier for it. A certifier checks a certificate related to the problem. A P problem must be an NP problem, but whether P=NP is still unknown (probably not).
An NP-Hard problem is a problem to which any NP problem is poly-reducible. An NP-Complete problem is a problem that belongs to both NP and NP-Hard. From the definition of poly-reducibility, we can deduce that if $A\leq_P B$:
(1) $B$ belongs to NPC implies $A$ belongs to NP;
(2) if $A$ is NPC and $B$ is NP, then $B$ is NPC.
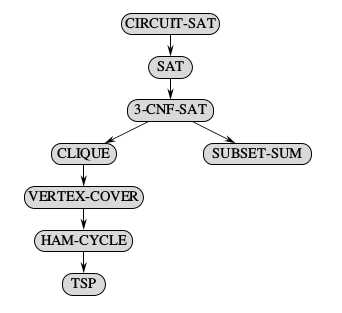
P=NP iff there exists an NPC problem that is polynomial-time solvable. Here are some famous NPC problems:
References:
1. Cutland, Nigel. Computability: an introduction to recursive function theory[M]. Cambridge: Cambridge University Press, 1980
2. Cormen, T. H. et al. Introduction to Algorithms [M] . 北京:机械工业出版社, 2006-09
Computability 6: Reducibility and NP Problems
标签:
原文地址:http://www.cnblogs.com/DevinZ/p/4539855.html