标签:
1.性质
红黑树是一种二叉查找树,但是每个节点增加一个表示结点颜色(红或黑)的字段,并且满足一下条件:
为方便处理边界条件,我们采用一个哨兵来表示NIL,如果某节点没有一个子结点或父结点,则该结点的相应指针指向NIL。
一棵有n个内结点(不包括NIL)的红黑树高度之多为2lg(n+1)。
2.旋转
在红黑树上执行插入或删除操作时,结果都可能违反红黑树的性质,我们需要改变树的指针结构来保持红黑树的性质。旋转是修正过程中会用到的操作,分为左旋和右旋,这里只介绍左旋操作,右旋刚好与左旋操作相反。下面是旋转的示意图
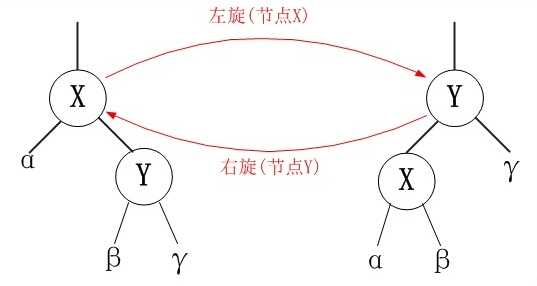
LEFT-ROTATE(T, x) y ← right[x] right[x] ← left[x] if left[y] != nil[T] p[left[y]] ← x p[y] ← p[x] if p[x] = nil[T] root[T] ← y else if x = left[p[x]] left[p[x]] ← y else right[p[x]] ← y left[y] ← x p[x] ← y
3.插入
插入操作与普通二叉树的插入操作接近,将新插入节点设置为红色(尽可能少违反二叉树性质),并在最后增加RB-INSERT-FIXUP(T, z)调节二叉树使其满足红黑树的性质。
RB-INSERT y ← nil[T] x ← root[T] while x != nil[T] do y ← x if key[z] < key[x] x ← left[x] else x ← right[x] p[z] ← y if y = nil[T] root[T] = z else if key[z] < key[y] left[y] ← z else right[y] ← z left[z] ← nil[T] right[z] ← nil[T] color[z] ← RED RB-INSERT-FIXUP(T, z)
标签:
原文地址:http://www.cnblogs.com/yitong0768/p/4561825.html