标签:
题目要求:
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle
1 [ 2 [2], 3 [3,4], 4 [6,5,7], 5 [4,1,8,3] 6 ]
The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
Note:
Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.
具体代码如下:

1 class Solution { 2 public: 3 int minimumTotal(vector<vector<int> > &triangle) { 4 int rows = triangle.size(); 5 if(rows == 0) 6 return 0; 7 8 int * dp = new int[rows]; 9 int szOfLastRow = triangle[rows - 1].size(); 10 for(int i = 0; i < szOfLastRow; i++) 11 dp[i] = triangle[rows - 1][i]; 12 13 for(int i = rows - 2; i > -1; i--) 14 { 15 int cols = triangle[i].size(); 16 for(int j = 0; j < cols; j++) 17 dp[j] = triangle[i][j] + min(dp[j], dp[j + 1]); 18 } 19 20 return dp[0]; 21 } 22 };
这个程序中最核心的地方在:
dp[j] = triangle[i][j] + min(dp[j], dp[j + 1]);
可以用图表示如下:
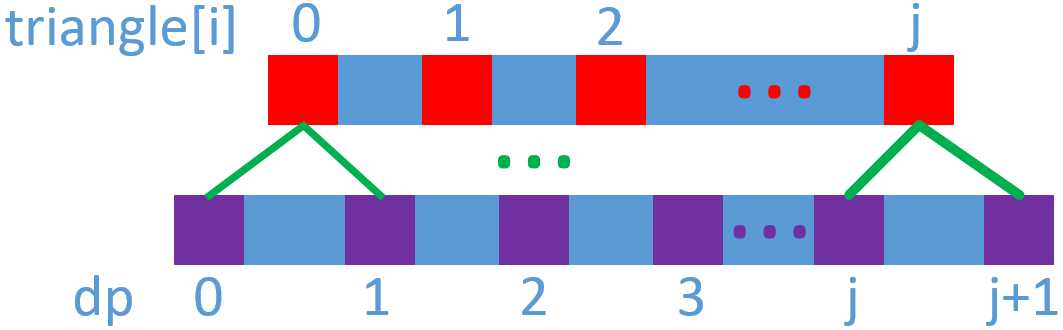
其中一个例子就是:
![]()
需要注意的就是这个例子中只改变的是dp[0],dp[1]并没有改变。
标签:
原文地址:http://www.cnblogs.com/xiehongfeng100/p/4562901.html