标签:
损失函数和风险函数
损失函数(loss function),代价函数(cost function)
用来度量预测错误的程度。常用的如下:
?
由于模型的输入、输出(X,Y)是随机变量,遵循联合分布P(X,Y),所以损失函数的期望是
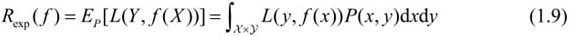
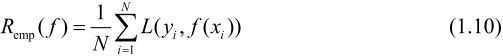
模型f(X)关于联合分布P(X,Y)的平均意义下的损失称之为
风险函数(risk function)或期望损失(expected loss)
模型f(X)关于训练数据集的平均损失称为
经验风险(empirical risk)或经验损失(empirical loss)
?
期望风险是模型关于联合分布的期望损失
经验风险是模型关于训练样本集的平均损失
根据大数定律,当样本容量N趋于无穷时,经验风险趋于期望风险
所以一个很自然的想法是用经验风险估计期望风险。要对经验风险矫正
这就关系到监督学习的两个基本策略:经验风险最小化和结构风险最小化
?
经验风险最小的模型是最优的模型,当样本大,经验风险最小化能保证有很好的学习效果,
比如,极大似然估计(maximum likelihood estimation)就是经验风险最小化的一个例子,
当模型是条件概率分布,损失函数是对数损失函数时,经验风险最小化就等价于极大似然估计
?
结构风险最小化是为了防止过拟合而提出来的策略。
结构风险最小化等价于正则化(regularization)。
结构风险在经验风险上加上表示模型复杂度的正则化项(regularizer)或罚项(penalty term)
复杂度表示了对复杂模型的惩罚用以权衡经验风险和模型复杂度。
结构风险小需要经验风险与模型复杂度同时小
?
?
过拟合与模型选择
如果追求提高对训练数据的预测能力,所选模型的复杂度则往往会比真模型更高
这种现象称为过拟合(over-fitting)。
过拟合是指学习时选择的模型所包含的参数过多,以致于出现这一模型对已知数据预测得很好,
但对未知数据预测得很差的现象。可以说模型选择旨在避免过拟合并提高模型的预测能力。
?
正则化
模型选择的典型方法是正则化。
正则化是结构风险最小化策略的实现,经验风险上加一个正则化项或罚项
正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化值就越大
比如,正则化项可以是模型参数向量的范数。
正则化的作用是选择经验风险与模型复杂度同时较小的模型。
正则化符合奥卡姆剃刀(Occam‘s razor)原理。
奥卡姆剃刀原理应用于模型选择时变为以下想法:在所有可能选择的模型中,能够
很好地解释已知数据并且十分简单才是最好的模型,也就是应该选择的模型。
从贝叶斯估计的角度来看,正则化项对应于模型的先验概率。
可以假设复杂的模型有较小的先验概率,简单的模型有较大的先验概率。
?
?
生成模型与判别模型
生成方法(generative approach)和判别方法(discriminative approach)。
所学到的模型分别称为生成模型(generative model)和判别模型(discriminative model)。
生成方法由数据学习联合概率分布P(X,Y),然后求出条件概率分布P(Y|X)作为预测的模型,即生成模型
典型的生成模型有:朴素贝叶斯法和隐马尔可夫模型
判别方法由数据直接学习决策函数f(X)或者条件概率分布P(Y|X)作为预测的模型,即判别模型
k近邻法、感知机、决策树、逻辑斯谛回归模型、最大熵模型、支持向量机、提升方法和条件随机场等
生成特点:生成方法可以还原出联合概率分布P(X,Y),而判别方法则不能
生成方法的学习收敛速度更快,即当样本容量增加的时候,学到的模型可以更快地收敛于真实模型;
当存在隐变量时,仍可以用生成方法学习,此时判别方法就不能用。
判别特点:判别方法直接学习的是条件概率P(Y|X)或决策函数f(X),直接面对预测,往往学习的准确率更高;
由于直接学习P(Y|X)或f(X),可以对数据进行各种程度上的抽象、定义特征并使用特征,因此可以简化学习问题。
?
?
?
?
?
?
?
?
?
?
?
标签:
原文地址:http://www.cnblogs.com/LauenWang/p/4564925.html