标签:
ZOJ Problem Set – 2770 Burn the Linked Camp
题目的大意为:
陆逊侦查得知刘备将自己的军队分为N个营,从左到右编号为1,2,3…N。第i个营有最大士兵数Ci,通过一段时间的观察,陆逊可以估算至少有k个士兵住在第i到第j个营地,最后陆逊必须要估算刘备的军队至少有多少士兵,以便应对。
输入:
有多个测试案例,在每个测试案例的第一行,有两个整数N(0<n<=1000)和M(0 <= M = 10000)。第二行中,有n个整数C1…CN。然后M行,每行有三个整数i,j,k(0 < <= j <= N,0≤k<2 ^ 31),这意味着从i到j营士兵总数量至少是K.
输出:
对于每一个测试案例,在一行一个整数,输出:根据陆逊的观察估算刘备军队最少的士兵数。然而,陆逊估计在输入数据可能很不精确。如果他的估计是不真实的,输出“Bad Estimations”在单一的一行。
解题思路:
题目要求从观察结果中求出刘备军队里士兵的最小值。由于每个营地都有能容纳士兵的最大值,存在不等约束关系,此题可以考虑用差分约束系统解题。
差分约束系统:
如果一个系统由n个变量和m个约束条件组成,其中每个约束条件都形如:
Xj-Xi<=Bk (i,j∈[1,n],k∈[1,m])
则称其为差分约束系统。
求解差分约束系统:
求解差分约束系统,可以转化成图论的单源最短路径问题,
Xj-Xi<=Bk
Xj<=Xi+Bk
类似最短路径的三角不等式
distance[v]<= distance[u]+weight[u,v]
即distance[v] - distance[u]<=weight[u,v]
因此,以每个变量Xi为结点,对于约束条件
Xj-Xi<=Bk 即 Xj<=Xi+Bk
连接一条边(i,j),权值为Bk
再增加一个源点A,A与所有顶点相连,权值均为0,如果图中存在负环,则无解,否则,从源点到其它顶点的单源最短路径就是问题的一组可行解。
设有N个营地,编号为 i(i=1、2、3…N), K(i)代表第i(i=1、2、3…N)个营地的士兵数加上编号小于i的所有营地的士兵数。
则第j(j=1、2、3…N)个营地的士兵数为K(j)-K(j-1)
若M(j)表示营地j能容纳的最大士兵数,则有不等关系:
K(j)-K(j-1)<=M(j)
变换得
K(j)<=K(j-1)+M(j)
为了避免第一个营地的特殊情况,我们增加一个编号为0且士兵数为0的营地,即K(1)-K(0)=K(1).这个营地只是辅助,对结果不产生影响。
我们设每个编号i的营地为顶点i(i=0,1,2…N),我们添加一个源点,源点到所有其他顶点都有一条有向边,权值为0,不需要保存该点,只是辅助解题,保证图的连通性。则K(j)和K(j-1)分别为从源点到j,j-1两点的最短路径权值,若营地j的士兵数为M(j),则有K(j)<=K(j-1)+M(j),可以从j到j-1连接一条有向边,权值为M(j),问题转化为求从源点到顶点j的单源最短路径。
因为从源点到点j的最短路径必定满足K(j)<=K(j-1)+M(j)
同理,从营地i到j之间至少有X个士兵,则有不等关系:
K(j)-K(i-1)>=X
变换为
K(i-1)<=K(j)-X
于是,从顶点j到顶点i-1连一条有向边,权值为-X,求解源点到j点的最短路径时必定也满足该不等式K(i-1)<=K(j)-X
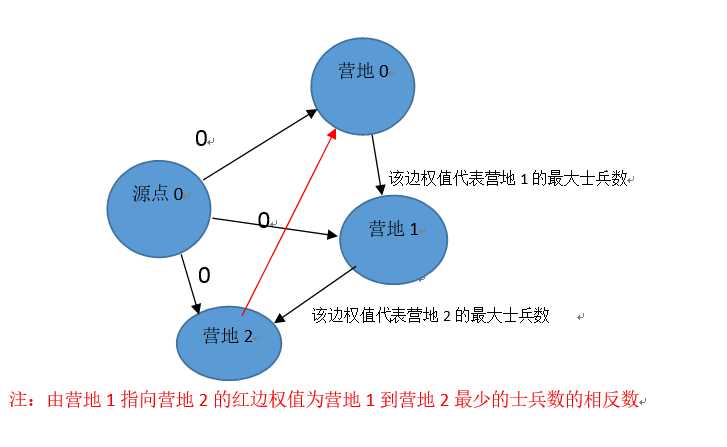
其中K(1),K(2)…K(N)为差分约束系统的一组解,当答案要求非负时,我们对每个解加上一个常数C便可。
最后源点到点N的最短路径便是问题的解,但实际上士兵数不能为负,因为求最少的士兵总数,我们可以加上一个最小的常数C,使得该组解非负。
当图中存在负权环时,问题无解。因为若存在负权环,不停地走这个环的话,最短路径趋向负无穷,显然不可能存在最短路径。
该题涉及负权边,用Bellman Ford算法求解最短路径较合适。
Bellman Ford算法思想是基于以下事实:
“两个点间如果存在最短路径,那么每个结点最多经过一次。”
也就是说,对n个结点的图,这条路不超过n-1条边。
如果一个结点经过了两个,说明我们走了一个圈:
如果该圈的权为正,显然不划算;
如果是负圈,不存在最短路径;
如果是零圈,去掉不影响最短路径。
路径边数上限为m的最短路径,可以通过由边数上限为m-1时的最短路径“外加一条边”来求,则最多只需要迭代n-1次就可以求出最短路径。
Bellman Ford算法伪代码如下:
//V(G)为图G的顶点集,E(G)为图G的边集
for i=0 to |V(G)|
for 每条边(u,v)属于E(G)//松弛每条边
if(distance[v]>distance[u]+weight[u,v])
distance[v]=distance[u]+weight[u,v]
end for
end for
for 每条边(u,v)属于E(G)//检查是否有负环
if(distance[v]>distance[u]+weight[u,v])
return false
end for
return true
算法时间复杂度O(VE)。
该算法简单容易理解,缺点是时间复杂度较高,这里可以用队列进行优化,本文重点是最短路径算法如何应用在差分约束系统,便不再赘述。
Bellman Ford算法用到松弛技术:
维护一个源点到所有其它点的距离表distance[],松弛一条边(u,v)的过程包括测试我们是否可以通过结点u对目前到v结点的最短路径distance[v]进行修改,如果通过u到达v的路径更短,则更新distance[v]。这样便是保证每两个结点都有
distance[v]<= distance[u]+weight[u,v]
伪代码如下:
if(distance[v]> distance[u]+weight[u,v])//不符合就调整
distance[v] = distance[u]+weight[u,v]
解题代码:
1 #include<stdio.h> 2 3 #include<vector> 4 5 int *disList;//求最短路径时维护的距离表 6 7 struct Edge{//边结构 8 9 int start;//起点 10 11 int end;//终点 12 13 int weight;//权值 14 15 }; 16 17 std::vector<Edge> E;//存放边集的容器 18 19 std::vector<Edge>::iterator it;//迭代器 20 21 bool bellmanford(int N)//求每个顶点到源点的最短路径 22 23 { 24 25 26 27 while(--N) //走N-1 条边 28 29 { 30 31 for (it = E.begin(); it != E.end();it++)//对每条边进行松弛 32 33 { 34 35 if (it->weight + disList[it->start]< disList[it->end]) 36 37 { 38 39 disList[it->end] = it->weight + disList[it->start]; 40 41 } 42 43 } 44 45 } 46 47 for (it = E.begin(); it != E.end(); it++)//若还能进行松弛,说明存在负环,无解 48 49 { 50 51 if (it->weight + disList[it->start]< disList[it->end]) 52 53 { 54 55 return false; 56 57 } 58 59 } 60 61 return true; 62 63 }; 64 65 void output(int N) 66 67 { 68 69 if (!bellmanford(N))printf("Bad Estimations\n"); 70 71 else//根据实际情况,兵营士兵数不能为负,将所有解化为正数 72 73 { 74 75 int min = disList[0]; 76 77 for (int i = 1; i <= N; i++) 78 79 { 80 81 if (min > disList[i])min = disList[i]; 82 83 } 84 85 if (min < 0) 86 87 { 88 89 disList[N] = disList[N] - min; 90 91 } 92 93 printf("%d\n", disList[N]); 94 95 } 96 97 }; 98 99 int main() 100 101 { 102 103 int N, M; 104 105 while (scanf_s("%d%d", &N,&M) ==2) 106 107 { 108 109 E.clear();//清空容器 110 111 disList = new int[N + 1]; 112 113 for (int i = 0; i <= N; i++)//初始化距离表 114 115 { 116 117 disList[i] = 0; 118 119 } 120 121 //输入数据 122 123 Edge e; 124 125 for (int i = 1; i <= N; i++) 126 127 { 128 129 scanf_s("%d", &e.weight); 130 131 e.start = i - 1; 132 133 e.end = i; 134 135 E.push_back(e);//营地i的最大士兵数为w,向矩阵图插入由i-1指向i权值为w的有向边 136 137 } 138 139 int a, b,c; 140 141 for (int i = 0; i < M; i++) 142 143 { 144 145 scanf_s("%d%d%d", &a,&b,&c); 146 147 e.start = b; 148 149 e.end = a - 1; 150 151 e.weight = -c; 152 153 E.push_back(e);//营地a与营地b之间至少士兵数为c,向矩阵图中插入由点b指向点a,权值为-c的有向边 154 155 } 156 157 output(N);//输出结果 158 159 delete[]disList;//释放内存 160 161 } 162 163 getchar(); 164 165 return 0; 166 167 }
ZOJ– 2770Burn the Linked Camp单源最短路径差分约束系统
标签:
原文地址:http://www.cnblogs.com/litianhan/p/4569834.html