标签:
k近邻法(k-nearest neighbor,k-NN)
输入:实例的特征向量,对应于特征空间的点;输出:实例的类别,可以取多类。
分类时,根据其k个最近邻的训练实例的类别,通过多数表决等方式进行预测。
实例类别已定,不具有显式的学习过程。k近邻法实际上利用训练数据集对特征
向量空间进行划分,并作为其分类的"模型"。
三个基本要素:k值的选择、距离度量及分类决策规则。
?
KDtree
实现k近邻法时,主要考虑的问题是如何对训练数据进行快速k近邻搜索。
k近邻法最简单的实现方法是线性扫描。这时要计算输入实例与每一个训练实例的距离。
为了提高k近邻搜索的效率,可以考虑使用特殊的结构存储训练数据,以减少计算距离的次数。
介绍kd树.
?
构造kd树
有数据集T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}
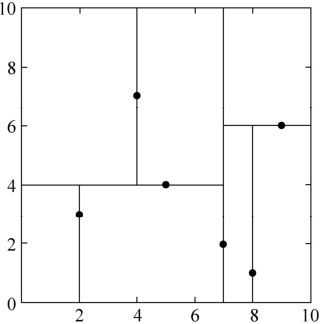
根结点对应包含数据集T的矩形,
选择x(1)轴,6个数据点的x(1)坐标的中位数是7,
以平面x(1)=7将空间分为左、右两个子矩形
接着,左矩形以x(2)=4分为两个子矩形,
右矩形以x(2)=6分为两个子矩形,如此递归
所得KD树如下:
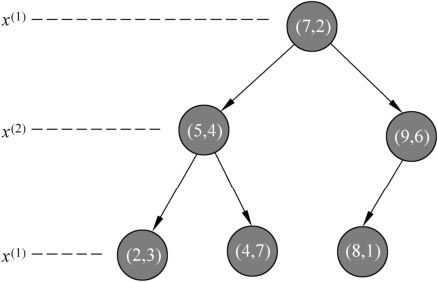
?
搜索kd树
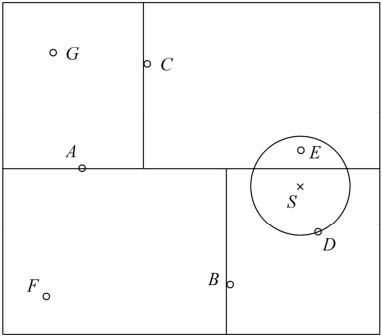
给定一个目标点,搜索其最近邻。
首先找到包含目标点的叶结点;然后从该叶结点出发,依次回退到父结点;
不断查找与目标点最邻近的结点,当确定不可能存在更近的结点时终止。
这样搜索就被限制在空间的局部区域上,效率大为提高。
?
包含目标点的叶结点对应包含目标点的最小超矩形区域。
以此叶结点的实例点作为当前最近点。
目标点的最近邻一定在以目标点为中心并通过当前最近点的超球体的内部
然后返回当前结点的父结点,若父结点的另一子结点的超矩形区域与超球体相交,
那么在相交的区域内寻找与目标点更近的实例点
如果存在这样的点,将此点作为新的当前最近点
算法转到更上一级的父结点,继续上述过程。
如果父结点的另一子结点的超矩形区域与超球体不相交,或不存在比当前最近点更近的点,则停止搜索。
?
?
?
?
?
?
?
?
?
标签:
原文地址:http://www.cnblogs.com/LauenWang/p/4570048.html