标签:
方老师重新开了一家农场,农场一共有N个节点和M条双向边,但是有一个很大的问题就是有比如一个农场A到达农场B只有一条路径,问至少添加多少条边使得任意两个农场之间的路径多于一条。
EOF结束。一行一个数表示至少需要添加多少条边。
| Sample Input | Sample Output |
|---|---|
7 7 1 2 2 3 3 4 2 5 4 5 5 6 5 7 |
2 |
N≤100000,M≤100000
解题思路:
我们先考虑原图连通的情况
首先跑一遍图,求出所有的桥,之后跑出边双连通分量数目.
将边双连通分量看成一个点.
之后我们考虑整个图,必然成了一棵树.
证明:
假设将边双连通分量看成一个点后图不是树,必然存在两个儿子之间连有边,这样就构成了边双连通,显然不合法,故命题正确.
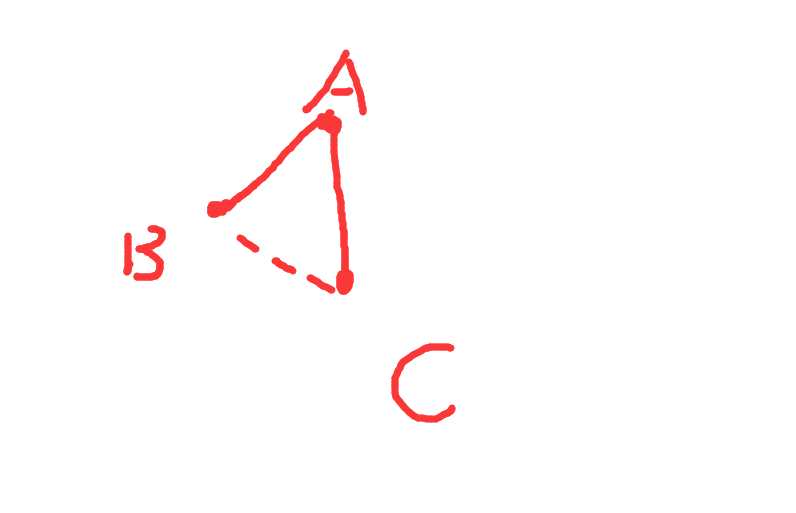
<B,C>之间不可能有边,否则构成了边双连通.
之后我们将问题转换为了树上至少连多少条边,使得树上任意两点的路径条数多于两条?
这样问题就很容易解了.
设树上的叶子有 N 个
If N ∈ (2 * k ) , ans = N / 2;
Else ans = ( N + 1 ) / 2
综合下得 ans = (N + 1 ) / 2;
为什么这样是对的呢?,我们将树上非叶的结点看成一个大圆圈,之后叶子,两两配对(找不到就自己和自己配),配对的顺序是第 x 个,和第 n – x + 1个,如图:
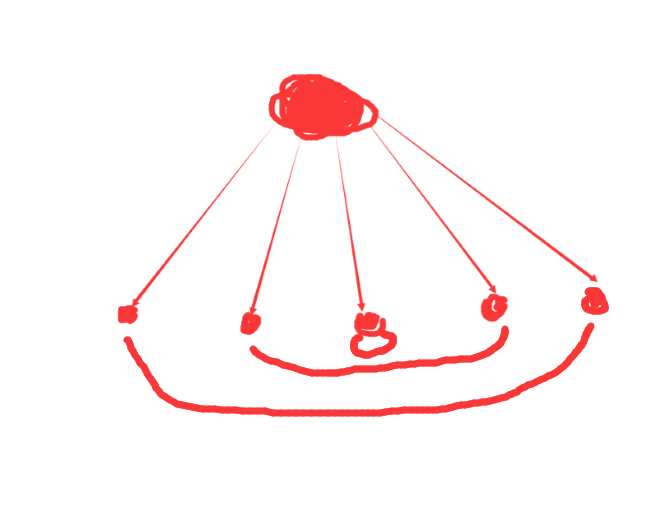
之后我们考虑,若原图不连通,如何求解?
还是看成大圆圈加几个根,把所有的叶子数加起来当成 N 就可以了.
这里有点要注意,我们给一旦连了一条边,其实我们就等于给大圆圈连了一条边了
<夜深了,就不证明了>
#include <iostream> #include <cstring> #include <cstdio> #include <algorithm> #include <vector> #include <set> #define pb push_back //#define localtest using namespace std; const int maxn = 1e5 + 50; int n,m,new_time[maxn],low[maxn],T,tot,degree[maxn],number[maxn]; bool use[maxn]; typedef pair<int,int> Etype; set<Etype>spj; typedef struct Edge { int v,isbridge; Edge(const int &v) { this->v = v; isbridge = 0; } }; vector<Edge>E[maxn]; int tarjan_dfs(int cur,int pre) { new_time[cur] = low[cur] = T++; for(int i = 0 ; i < E[cur].size() ; ++ i) { int nextnode = E[cur][i].v; if (!new_time[nextnode]) //树边 { int lowv = tarjan_dfs(nextnode,cur); if (lowv > new_time[cur]) { E[cur][i].isbridge = 1; #ifdef localtest cout << cur << " - " << nextnode << " is a bridge " << endl; #endif use[cur] = true , use[nextnode] = true; } low[cur] = min(low[cur],lowv); // updata } else if(new_time[nextnode] < new_time[cur] && nextnode != pre) //反向边 low[cur] = min(low[cur],low[nextnode]); } return low[cur]; } int main(int argc,char *argv[]) { while(~scanf("%d%d",&n,&m)) { spj.clear(); for(int i = 1 ; i <= m ; ++ i) { int u,v; scanf("%d%d",&u,&v); if (u > v) swap(u,v); Etype temp(u,v); if (spj.count(temp)) continue; else spj.insert(temp); E[u].pb(Edge(v)) , E[v].pb(Edge(u)); } memset(new_time,0,sizeof(new_time)); memset(number,0,sizeof(number)); memset(use,false,sizeof(use)); memset(degree,0,sizeof(degree)); T = 1; for(int i = 1 ; i <= n ; ++ i) if (!new_time[i]) tarjan_dfs(i,0); //跑割桥 for(int i = 1 ; i <= n ; ++ i) { for(int j = 0 ; j < E[i].size() ; ++ j) { int nextnode = E[i][j].v; if (low[i] != low[nextnode]) //缩点 { degree[low[i]] ++ ; degree[low[nextnode]] ++ ; } } } int leaf = 0; for(int i = 1 ; i <= n ; ++ i) if (degree[i] == 2) leaf++; printf("%d\n",(leaf+1)/2); for(int i = 1 ; i <= n ; ++ i) E[i].clear(); } return 0; }
UESTC_方老师和农场 2015 UESTC Training for Graph Theory<Problem L>
标签:
原文地址:http://www.cnblogs.com/Xiper/p/4570670.html