Naive Bayes、神经网络初步、SVM

标签：

PART 1    Naive Bayes

还是上节课说过的垃圾邮件分类问题，分为两种事件模型：

1.1.多变量Bernouli事件模型

　　【就是上节课介绍的

　　维护一个长长长长长的dictionary

　　对于某个样本(x,y)，x[i]=0or1表示dictionary第i个词是否在样本邮件中出现过，y=0or1表示样本是不是垃圾邮件

　　在这个模型中，Xi取值只有0or1，因此 $x_{i} | y$ 是Bernouli分布

　　$ANS= P\left( y\right) \prod ^{n}_{i=1}P\left( x_{i} | y\right)$

1.2.多项式事件模型

　　还是需要长长长长长的dictionary【设dictionary中有50000个词】

　　对于某个样本(x,y)，x[j]表示样本text中第j个位置出现的是哪个词(编号) $\in [1,50000] $

　　注：约定 $x^{\left( i\right) }_{j}$ 表示第i个样本中第j个位置出现的哪个词

　　在这个模型中，Xi可以取50000种值，因此 $x_{i} | y$ 是多项式分布

　　$ANS= P\left( y\right) \prod ^{n}_{i=1}P\left( x_{i} | y\right)$

　　在这个模型中涉及的参数：

　　$\phi_{y}=p\left( y=1\right)$

　　$\phi_{i|y=1}=p\left(x_{j}=i | y=1\right)$

　　$\phi_{i|y=0}=p\left(x_{j}=i | y=0\right)$ 　　【注意：words具体出现的位置和顺序并不会影响结果

　　对于i个样本的情况，可以求出似然函数，并求最大似然

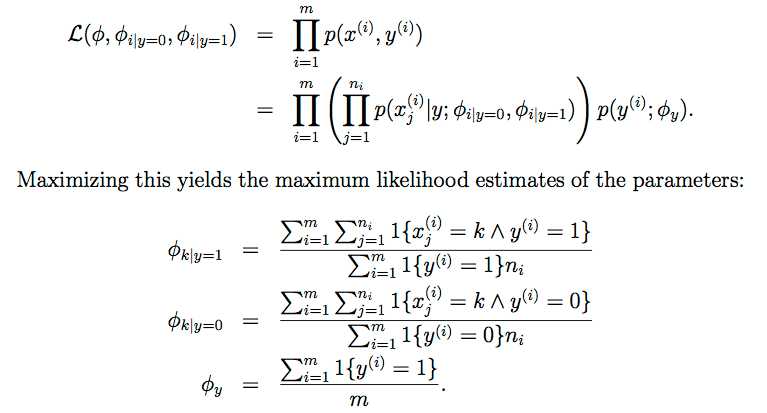
　　对这个结果也可以施行Laplace平滑，得　　【这里的|V|就是dictionary中单词的数目，就是上文中的50000

Naive Bayes、神经网络初步、SVM

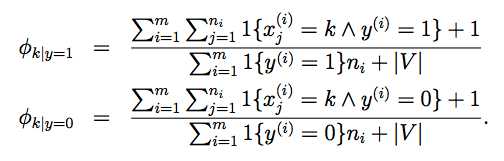
标签：

原文地址：http://www.cnblogs.com/pdev/p/4571961.html