标签:
提升树是以分类树或回归树为基本分类器的提升方法
提升树被认为是统计学习中性能最好的方法之一
提升方法实际采用加法模型(基函数的线性组合)与前向分步算法
以决策树为基函数的提升方法称为提升树
?
对分类问题决策树是二叉分类树
对回归问题决策树是二叉回归树
?
提升树模型可以表示为决策树的加法模型:

T(x;Θm)表示决策树;
Θm为决策树的参数;
M为树的个数。
提升树算法采用前向分步算法。
首先确定初始提升树f0(x)=0,第m歩的模型是

fm-1(x)为当前模型,通过经验风险极小化确定下一棵决策树的参数Θm,
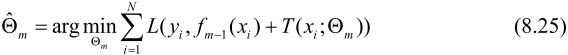
?
?
下面讨论针对不同问题的提升树学习算法,其主要区别在于使用的损失函数不同。
包括用平方误差损失函数的回归问题,用指数损失函数的分类问题
回归问题的提升树:
训练数据集T={(x1,y1),(x2,y2),…,(xN,yN)}
如果将输入空间x划分为J个互不相交的区域R1,R2,…,RJ,并且在每个区域上确定输出的常量cj,那么树可表示为

参数Θ={(R1,c1),(R2,c2),…,(RJ,cJ)}表示树的区域划分和各区域上的常数。
J是回归树的复杂度即叶结点个数。
利用如下前向分布算法:
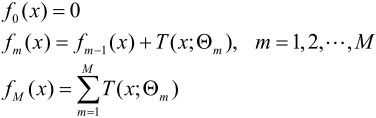
在前向分步算法的第m步,给定当前模型fm-1(x),需求解
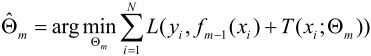
得到Θ,即第m棵树的参数。
当采用平方误差损失函数时:
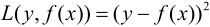
其损失变为:
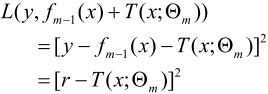
这里:

是当前模型拟合数据的残差(residual)。
所以,对回归问题的提升树算法来说,只需简单地拟合当前模型的残差。
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
标签:
原文地址:http://www.cnblogs.com/LauenWang/p/4574211.html