标签:
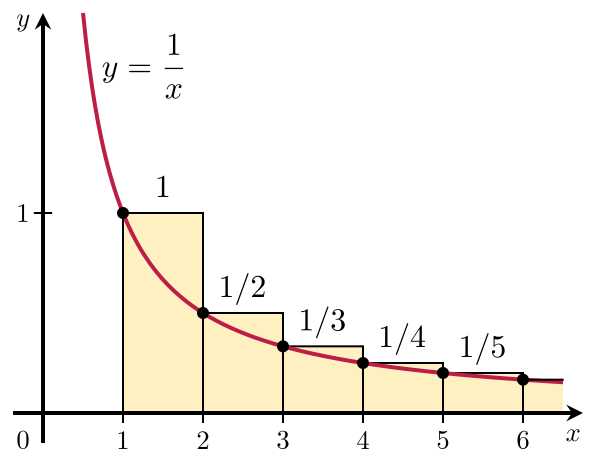
(图片来自 Wikipedia)
观察这张图:
第一个矩形的面积是 1, 第二个是 1/2, 第三个是 1/3, ……第 k 个是 1/k; 这 k 个矩形的面积之和,显然大于它们下面的积分 \(\int_{1}^{k+1} \frac{1}{x}\mathrm{d}x\)
如果拿掉第一个矩形,把剩下的矩形都翻到左边来,这 k - 1 个矩形的面积之和,显然小于它们上面的积分 \(\int_{1}^{k} \frac{1}{x}\mathrm{d}x\)
由此可得:
\(ln(k+1) < 1+\frac{1}{2}+\frac{1}{3}+ ... + \frac{1}{k} < ln(k)+1\)
照葫芦画瓢,还可以得到很多不等式,比如:
\(1+\frac{1}{4}+\frac{1}{9}+...+\frac{1}{n^{2}}>\int_{1}^{n+1}\frac{1}{x^{2}}\mathrm{d}x=\frac{1}{2}-\frac{1}{n+1}\)
\(1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{n}}<1+\int_{1}^{n}\frac{1}{\sqrt{x}}\mathrm{d}x=2\sqrt{n}-1<2\sqrt{n}\)
这两个不等式的证明都是放缩裂项的经典例题,不过显然用积分更好证,而且有直观的几何意义。
标签:
原文地址:http://www.cnblogs.com/li-hua/p/4574432.html