标签：des   style   blog   http   color   strong   

简易解释：在曲面中插入一个平面所形成的轮廓，即是该轮廓的水平集表示，可见，该轮廓的水平集表示有多个。对于图像分割，在图像力的驱动下曲面进行更新。

轮廓的数学表达有隐式和显式两种表达。用曲面演化代替Front （C）演进。

C(t) = {(x, y)|φ(x, y, t) = 0}

?φ/ ?t + F|?φ| =0 (1)

φ(x, y, 0) = φ0(x, y) 方程的本质是什么？ 几何解释是什么

edge-based level set

?φ /?t = g(?I)|?φ| (div ( ?φ /|?φ| _ + ν ) (2)

φ(x, y, 0) = φ0(x, y) based on mean curvature motion by Caselles et 1993

?φ /?t = |?φ| (?ν + ν/ (M1 ? M2) )(|?G?I| ? M2) (3)

φ(x, y, 0) = φ0(x, y)???? Malladi et 1993

?

?φ /?t = |?φ|div （g(I) ?φ /|?φ| _ + νg(|?I|) = g(I)|?φ|div ( ?φ /|?φ| _+?g(I) · ?φ + νg(|?I|)

φ(x, y, 0) = φ0(x, y) (4) Kichenassamy et 1995 and Caselles et 1995

An abstract representation common to all edge-based partial differential equation(PDE) is as follows:

?φ /?t = ?αA(x) · ?φ ? βP(x)|?φ| + γZ(x)κ|?φ| (5)

φ(x, y, 0) = φ0(x, y) A is an advection term ; P is a propagation(expansion) term ; Z is a spatial modifier term for the mean curvature k.

region-based level-sets

Region-based level-sets segment the image into objects based on region statistics (rather than just object edges) of intensity, tex- ture, or color values.

F(c1, c2, φ) = _Inside(C) (I(x) ? c1)²dx + _Outside(C) (I(x) ? c2)²dx + ν · Area(C) +μ · Length(C) (6)

?

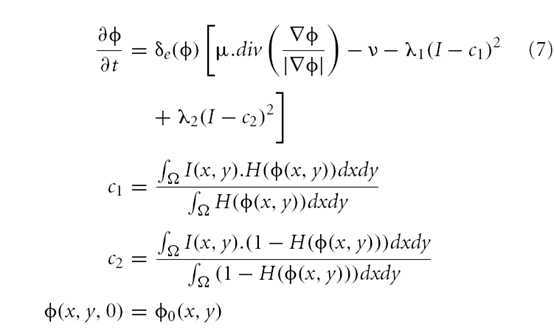
by Chan and Vese 2001

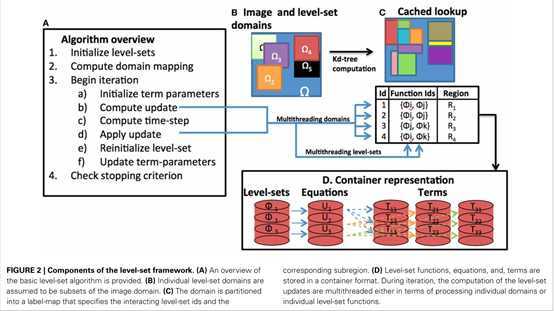
3.1 DOMAIN REPRESENTATION …… 不懂

3.2 水平集函数

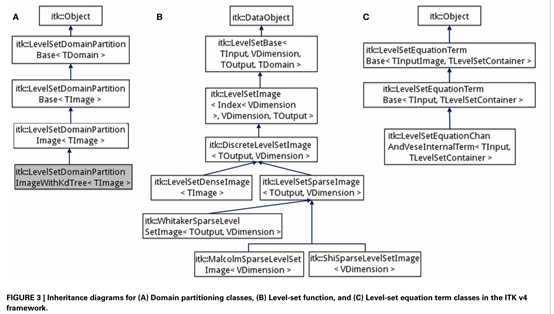
定义了一个抽象的水平集函数基类 itk：：LevelSetBase

所有的水平集函数类实现具体的成员函数返回the level-set value [φ(x,y)], gradient(?φ),Hessian(? ² φ),Laplacian(φ _xx + φ _yy ),gradient norm(|?φ|), and mean curvature (κ = div(?φ/|?φ| )) given its underlying representation (continuous or discrete image or mesh). Thus,the level-set equation, term, and evolution classes are independent of the underlying domain representation which facilitates the implementation of a wide variety of level-set methods.

图像的离散化表示itk：：DiscreteLevlSetImage 被具体实现为Dense 和Sparse 情况。三种Sparse的表示：Whitaker 、Shif、Malcolm。（narrow-band）

3.2.1图像到水平集转换 BinaryImageToLevelSetAdaptorbase

3.3

在图像子集域内进行水平集演化，划分成不同子域。 A helper base class (LevelSetDomainPartitionBase) is used to define the location and size of the level-set domains relative to ? (Figure3A).

Each grid point stores a list of the active level-set function ids. For the case when there are thousands of level-sets, populating a list image by checking overlap at each pixel is time-consuming. Therefore, we further specialized into a class itk::LevelSetDomainPartitionImageWithKdTree. This class uses a Kd-tree data structure that contains the centroids of the level-set domains. The Kd- tree is used to query nearby level-set functions at each pixel and check for overlap.This enables the simultaneous evolution of thousands of level-set functions thereby expanding the applicability of level-set procedures to tracking large numbers of objects and in large images. Note that there is an initial overhead associated with building the Kd-tree that can be avoided for cases involving a small number of level-set functions.

3.4 terms

水平集方程是各项的加权和。The term base class implements functions [Evaluate(.)] for computing the contribution from a term toward the level-set update.

3.5 container-based design

Container 是什么？

Different types of terms arising from edge-based and region-based level-set methods such as the propaga-

tion, Laplacian, advection, curvature, and region-based terms described in Equations 4 and 7 derive directly from LevelSetEquationTermBase:

we used containers to store level-set function objects, equation objects, and their constitutive terms。

Leve-set container term containers level-set equation container

3.6 Level-set evolution

3.7 stopping criterion

itk::StoppingCriterionBase

3.8 user-interaction

3.9 visualization

计划：怎样理解水平集方法 ITK Level set V4 框架介绍,布布扣,bubuko.com

计划：怎样理解水平集方法 ITK Level set V4 框架介绍

标签：des   style   blog   http   color   strong   

原文地址：http://www.cnblogs.com/taopanpan/p/3818191.html