标签:
在上一回中小Hi和小Ho控制着主角收集了分散在各个木桥上的道具,这些道具其实是一块一块骨牌。

主角继续往前走,面前出现了一座石桥,石桥的尽头有一道火焰墙,似乎无法通过。
小Hi注意到在桥头有一张小纸片,于是控制主角捡起了这张纸片,只见上面写着:
将M块骨牌首尾相连放置于石桥的凹糟中,即可关闭火焰墙。切记骨牌需要数字相同才能连接。 ——By 无名的冒险者
小Hi和小Ho打开了主角的道具栏,发现主角恰好拥有M快骨牌。
小Ho:也就是说要把所有骨牌都放在凹槽中才能关闭火焰墙,数字相同是什么意思?
小Hi:你看,每一块骨牌两端各有一个数字,大概是只有当数字相同时才可以相连放置,比如:

小Ho:原来如此,那么我们先看看能不能把所有的骨牌连接起来吧。
第1行:2个正整数,N,M。分别表示骨牌上出现的最大数字和骨牌数量。1≤N≤1,000,1≤M≤5,000
第2..M+1行:每行2个整数,u,v。第i+1行表示第i块骨牌两端的数字(u,v),1≤u,v≤N
第1行:m+1个数字,表示骨牌首尾相连后的数字
比如骨牌连接的状态为(1,5)(5,3)(3,2)(2,4)(4,3),则输出"1 5 3 2 4 3"
你可以输出任意一组合法的解。
5 5 3 5 3 2 4 2 3 4 5 1
1 5 3 4 2 3
小Ho:这种简单的谜题就交给我吧!
小Hi:真的没问题么?
<10分钟过去>
小Ho:啊啊啊啊啊!搞不定啊!!!骨牌数量一多就乱了。
小Hi:哎,我就知道你会遇到问题。
小Ho:小Hi快来帮帮我!
小Hi:好了,好了。让我们一起来解决这个问题。
<小Hi思考了一下>
小Hi:原来是这样。。。小Ho你仔细观察这个例子:

因为相连的两个数字总是相同的,不妨我们只写一次,那么这个例子可以写成:3-2-4-3-5-1。6个数字刚好有5个间隙,每个间隙两边的数字由恰好对应了一块骨牌。
如果我们将每一个数字看作一个点,每一块骨牌看作一条边。你觉得是怎么样的呢?
小Ho:以这个例子来说的话,就是:
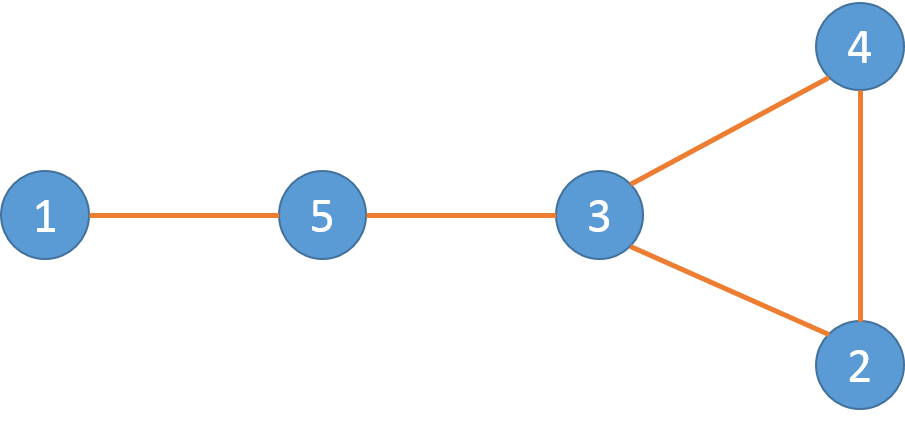
要把所有的骨牌连起来,也就是把所有的边都走一次。咦,这不是欧拉路问题么!
小Hi:没错,这问题其实就是一个欧拉路的问题,不过和上一次不一样的在于,这一次我们要找出一条欧拉路径。
小Ho:那我们应该如何来找一条路径呢?
小Hi:我们还是借用一下上次的例子吧
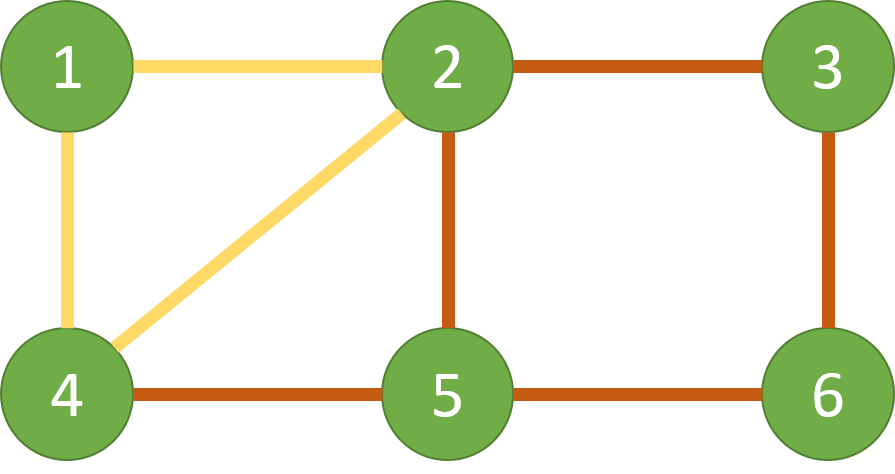
使用我们上一次证明欧拉路判定的方法,我们在这个例子中找到了2条路径:
L1: 4-5-2-3-6-5 L2: 2-4-1-2
假设我们栈S,记录我们每一次查找路径时的结点顺序。当我们找到L1时,栈S内的情况为:
S: 4 5 2 3 6 5 [Top]
此时我们一步一步出栈并将这些边删除。当我们到节点2时,我们发现节点2刚好是L1与L2的公共节点。并且L2满足走过其他边之后回到了节点2。如果我们在这个地方将L2先走一遍,再继续走L1不就刚好走过了所有边么。
而且在上一次的证明中我们知道,除了L1之外,其他的路径L2、L3...一定都满足起点与终点为同一个点。所以从任意一个公共节点出发一定有一条路径回到这个节点。
由此我们得到了一个算法:
在原图中找一个L1路径
从L1的终点往回回溯,依次将每个点出栈。并检查当前点是否还有其他没有经过的边。若存在则以当前点为起点,查找L2,并对L2的节点同样用栈记录重复该算法。
当L1中的点全部出栈后,算法结束。
在这里我们再来一个有3层的例子:
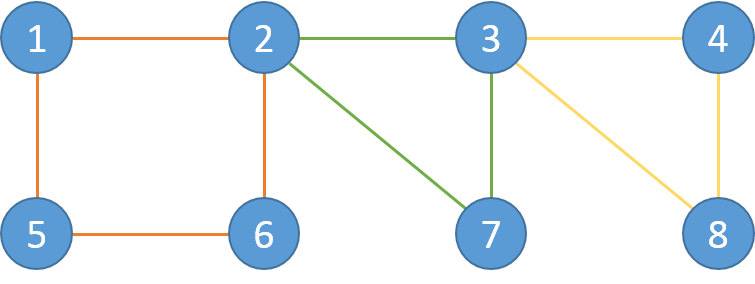
在这个例子中:
L1: 1-2-6-5-1 L2: 2-3-7-2 L3: 3-4-8-3
第一步时我们将L1压入栈S,同时我们用一个数组Path来记录我们出栈的顺序:
S: [1 2 6 5 1] Path:
然后出栈到节点2时我们发现了2有其他路径,于是我们把2的另一条路径加入:
S: 1 [2 3 7 2] Path: 1 5 6
此时L2已经走完,然后再开始弹出元素,直到我们发现3有其他路径,同样压入栈:
S: 1 2 [3 4 8 3] Path: 1 5 6 2 7
之后依次弹出剩下的元素:
S: Path: 1 5 6 2 7 3 8 4 3 2 1
此时的Path就正好是我们需要的欧拉路径。
小Ho:原来这样就能求出欧拉路,真是挺巧妙的。
小Hi:而且这个算法在实现时也有很巧妙的方法。因为DFS本身就是一个入栈出栈的过程,所以我们直接利用DFS的性质来实现栈,其伪代码如下:
DFS(u): While (u存在未被删除的边e(u,v)) 删除边e(u,v) DFS(v) End PathSize ← PathSize + 1 Path[ PathSize ] ← u
小Ho:这代码好简单,我觉得我可以实现它!
小Hi:那么实现就交给你了
小Ho:没问题!交给我吧
标签:
原文地址:http://www.cnblogs.com/yanglingwell/p/4575649.html