标签:
一、partition的划分问题
如何划分partition对block数据的收集有很大影响。如果需要根据block来加速task的执行,partition应该满足什么条件?
参考思路1:range partition
1、出处:
IBM DB2 BLU;Google PowerDrill;Shark on HDFS
2、规则:
range partition遵循三个原则:1、针对每一列进行细粒度的范围细分,防止数据倾斜和工作量倾斜;2、每一个partition分配的列是不同的;3、需要针对数据相关性和过滤关联性来考虑partition的划分。
实现方法可以参考思路3中的Spark的实现。
3、简单思考:
这样划分partition需要很多额外的工作,如果针对我的设计是不需要这么多的,唯一需要考虑的就是第一点:避免数据倾斜和工作量倾斜。
参考思路2:Fine-grained Partitioning ( one of horizontal partitioning )
1、出处:
Fine-grained Partitioning for Aggressive Data Skipping (ACMSIGMOD14)
2、规则:
fine-grained partitioning的划分目的很明确:划分成细粒度的、大小平衡的block,而划分的依据是让查询操作(该partition方式针对 shark query制定)更大程度上的跳过对该block的扫描。具体的方法是:
(1)从之前频繁使用的过滤集(文章已证明一部分典型的过滤能够用来决策)中抽取过滤的判断条件作为特征;
(2)根据抽取的特征对数据进行重计算,产生特征向量,从而将问题修改成最优解的问题;
示例如下:每个partition对应一个Feature为0,即不满足该特征,如果利用该Feature扫描时可以直接跳过改partition。
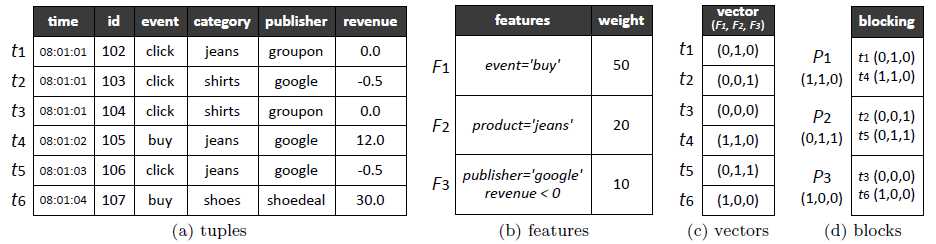
3、简单思考:
首先,fine-grained具有以下特点:(1)由一个额外的进程守护,工作于数据加载时或者某个最新的任务(这个任务必然是对partition重新提出了请求,诸如显示的用户partition操作)执行时;(2)该方法针对partition的形成、block的形成同时适用;(3)从filter中抽取典型的特征来划分数据。
然后分析该方法的思想,该方法利用所需要的信息,即filter特性与skip block的特性,来将划分block和partition,具有很高的参考价值。而我所需要的数据特性应该包括数据的重要性、启动task所需要的数据的完整性、启动task所需要的block块的完整性,更确切的说应该是block数据完成了多少就可以启动task了,如何判断这个量?
参考思路3:Spark实现的Hash Partition
1、出处:
Spark1.3.1源码解析,Spark默认的自带Partitioner。实际上,Spark1.3.1在这一块也实现了RangePartitioner,而HashPartitioner利用的还是Range Partition。
2、规则:
首先,为了粗略达到输出Partition之间的平衡,需要定义一些参数,这些参数辅助决策一个RDD结果分配到每个Partition的样本数:
sampleSize,限定取样的大小,min(20*partitions,1M);
sampleSizePerPartition,Partition取样样本数,ceil(3*sampleSize/partitions),通过向上取整表示允许超过取样数目少量;
sketched,用来描述一个rdd的结果,包括了(partition id, items number, sample),sample是根据前面的参数决定的;
(key,weight)和imbalancedPartitions,分别是一个buffer数组和mutable类型值,分别存放平衡的Partition的权重和非平衡的Partition,平衡与否根据Partition大小与平均Partition大小的关系判断,权重=Partition大小/取样大小。
具体看看如何实现平衡的判断:
val fraction = math.min(sampleSize / math.max(numItems, 1L), 1.0)
val balance_or_not = if(fraction * numItems > sampleSizePerPartition) true else false
针对不平衡的Partition重新取样,取样后权重为1/fraction。
其次,需要注意的是,Partition中利用了一个implicitly方法,该方法获取RangPartition中隐藏的参数值:Ordering[ClassTag]。改参数值用来写入和读取Spark框架中的数据流。通过writeObject和readObject可以控制写入和读取Partition中的数据。
最后,决策Partition的bounds时利用的是Object RangePartitioner中的determineBounds方法,该方法利用weight的值来平衡block的大小,然后放入Partition中,进而平衡Partition的大小。
3、简单思考:
Spark自带的Partition策略是利用hashcode获取Partition id的RangePartition,RangePartition采用取样权重的方法来平衡各个Partition的大小,但是并未考虑Partition内部数据的关联度,也就是Block层面的决策没有体现在这里,需要进一步考虑如何按block优化。
二、如何利用Partition和Block的划分策略——重点论文:The Power of Choice in Data-Aware Cluster Scheduling,OSDI14
前文讲了三个如何划分Partition和Block的方法,但是划分之后如何应用其优化,除了上述提到的相应文章,与开题更加对应的是OSDI14年的文章The Power of Choice in Data-Aware Cluster Scheduling。该论文设计实现的系统为KMN,因此下文以KMN代替该论文。
1、概要
原始的Spark中的task在需要资源(该资源为上游stage的output)时,由调度器拉取task需要的资源数目,然后交付给task;而KMN的策略是,调度器拉取的是全部的资源中的数学组合,数量上仍旧是task所需的资源数,大体的关系如下图。
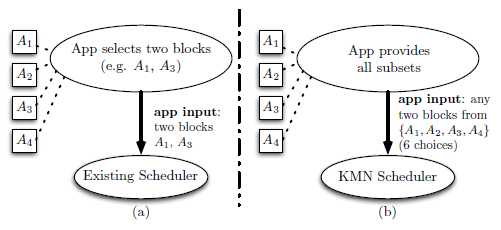
因此,KMN的特色之处在于choice,如何组合最优的block给Scheduler,然后调度给task,达到最高的效率。进而将问题转化为NP问题。需要注意的是,KMN选择choice时是根据全部的block来决策,那么必须等全部的block产生,即上游stage运行完成后才能决策。这样KMN就需要考虑上游Straggler的影响了,很遗憾的是,KMN针对的是近似解问题,从而导致它决定将Straggler丢弃来加快速度。
2、详细实现
KMN核心在于数据感知的choice,其决策分Input Stage和Intermediate Stage两种基本场景,决策Memory Locality和NetWork Blance两个方面。
(1)Input Stage
Input Stage中通过组合block的决策可以在各种集群利用率下保证很高的数据本地性,论文以N中采样K个block为例说明自然采样和用户自定义采样条件下的数据本地性概率。
(2)Intermediate Stage
Intermediate Stage需要考虑其上下游的Stage。KMN为上游Stage设置了额外的task,需要确认额外的task对Block决策调度的影响,文章以M个task和K个block的模型,分析M/K下上游额外task对cross-rack skew,即倾斜度造成的干扰。然后,根据上游Stage的输出选择最优的Block,此时问题转化为一个NP困难问题。最后,需要处理上游Stage的Straggler问题,因为Straggler的出现会导致Intermediate Stage的block的决策受到影响。文章对比Straggler的出现和额外的choice决策的时间,发现Straggler的影响占20%-40%,因此文章采用如下方法解决该问题:当M个上游task中的K个task执行完成后就启动下游task。实际上就是通过加速Stage的执行来加快下游stage的启动时间。
Spark的Straggler深入学习(2):思考Block和Partition的划分问题——以论文为参考
标签:
原文地址:http://www.cnblogs.com/zx247549135/p/4543507.html