标签：
题意：电影院卖票。一张票50元。一开始没有零钱。有m+n个人买票，m个人拿50元的钞票，n个人拿100的。问队伍有多少种排列方式可以使得卖票能顺利进行下去。
mark：如果要使得卖票的行为进行下去，对于任意前k个人，必须满足这k个人里面拿100的人数不多于拿50的人数。结果会是一个大整数，要用高精度。
公式是n!m!(m-n+1)/(m+1)。推导比较难想，和卡特兰数有关，网上有一篇文档详细写明了这个过程：http://daybreakcx.is-programmer.com/posts/17315.html
最后一段摘录如下：
n+m个人排队买票，并且满足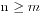
，票价为50元，其中n个人各手持一张50元钞票，m个人各手持一张100元钞票，除此之外大家身上没有任何其他的钱币，并且初始时候售票窗口没有钱，问有多少种排队的情况数能够让大家都买到票。
这个题目是Catalan数的变形，不考虑人与人的差异，如果m=n的话那么就是我们初始的Catalan数问题，也就是将手持50元的人看成是+1，手持100元的人看成是-1，任前k个数值的和都非负的序列数。
这个题目区别就在于n>m的情况，此时我们仍然可以用原先的证明方法考虑，假设我们要的情况数是
，无法让每个人都买到的情况数是
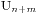，那么就有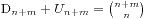
，此时我们求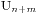，我们假设最早买不到票的人编号是k，他手持的是100元并且售票处没有钱，那么将前k个人的钱从50元变成100元，从100元变成50元，这时候就有n+1个人手持50元，m-1个手持100元的，所以就得到
，于是我们的结果就因此得到了，表达式是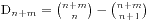
。
# include <stdio.h>
# include <string.h>
char s[1010], buff[1010] ;
#define mul(s, x){ for (cc = 0, len = strlen(s), j = len-1 ; j >= 0 ; j--) cc = (s[j]-'0') * (x) + cc , s[j] = cc%10 + '0' , cc/=10 ; if (cc) sprintf (buff, "%d", cc), strcat(buff, s), strcpy(s, buff);}
int main ()
{
int n, m, i, j, nCase = 1, cc, len ;
while (~scanf ("%d%d", &m, &n) && (m||n))
{
if (m < n) strcpy(s, "0") ;
else{
strcpy(s, "1") ;
for (i = 1 ; i <= (m+n) ; i++) if (i != m+1)
mul(s, i) ;
if (n != 0) mul (s, m-n+1) ;
}
printf ("Test #%d:\n%s\n", nCase++, s) ;
}
return 0 ;
}标签：
原文地址：http://blog.csdn.net/a197p/article/details/46502975
