标签:
线性回归诊断--R
【转载时请注明来源】:http://www.cnblogs.com/runner-ljt/
Ljt 勿忘初心 无畏未来
作为一个初学者,水平有限,欢迎交流指正。
R--线性回归诊断(一) 主要介绍了线性回归诊断的主要内容和基本方法。
本文作为R中线性回归诊断的进一步延伸,将主要介绍用car包中的相关函数就行线性回归诊断。
>
> head(bank)
y x1 x2 x3 x4
1 1018.4 96259 2239.1 50760 1132.3
2 1258.9 97542 2619.4 39370 1146.4
3 1359.4 98705 2976.1 44530 1159.9
4 1545.6 100072 3309.1 39790 1175.8
5 1761.6 101654 3637.9 33130 1212.3
6 1960.8 103008 4020.5 34710 1367.0
> fline<-lm(y~x1+x2+x3+x4,data=bank)
>
正太性检验:
qqPlot
相较于 plot()函数,画更为精确的学生化残差图。
> qqPlot(fline)
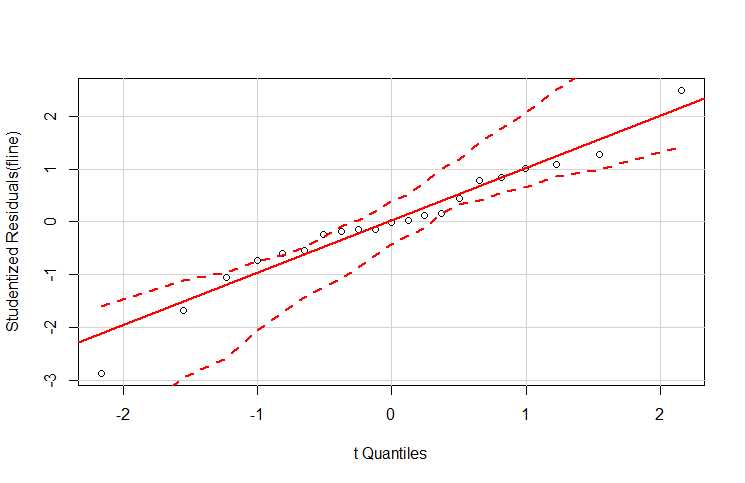
直线两侧的虚曲线代表置信区间,落在两曲线外的点可以认为是离群点。
线性检验:
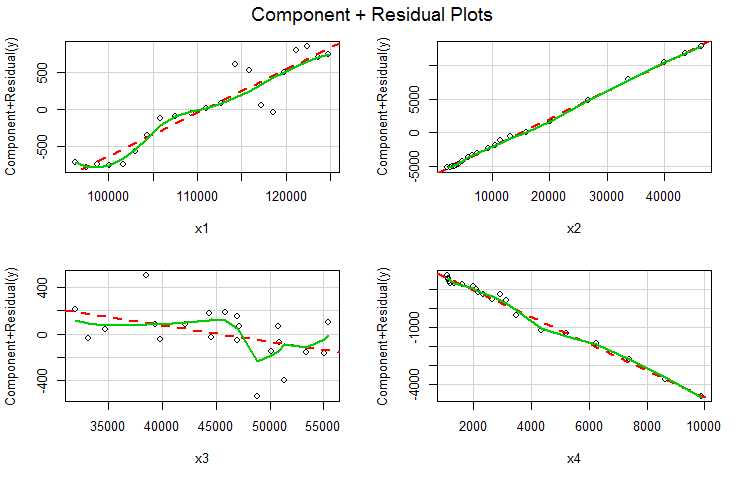
crPlots
可通过成分残差图即偏残差图,判断因变量与自变量之间是否呈非线性关系,这种处理在检验线性关系的时候可以排除掉其他自变量的影响。
散点的 横轴为Xi ,纵轴为 Θi*Xi +ε
可以通过红线和绿线趋势是否一致来判断线性关系。(红线为 y=Θi*Xi ; 绿线为散点的趋势曲线)
> crPlots(fline)
异方差检验:
ncvTest
原假设:随机误差的方差不变 ------- P值>0.05 则接受原假设,即不存在明显的异方差现象。
> > ncvTest(fline) Non-constant Variance Score Test Variance formula: ~ fitted.values Chisquare = 0.2017512 Df = 1 p = 0.653311 >
P值=0.653311>0.05 故不存在异方差情况。
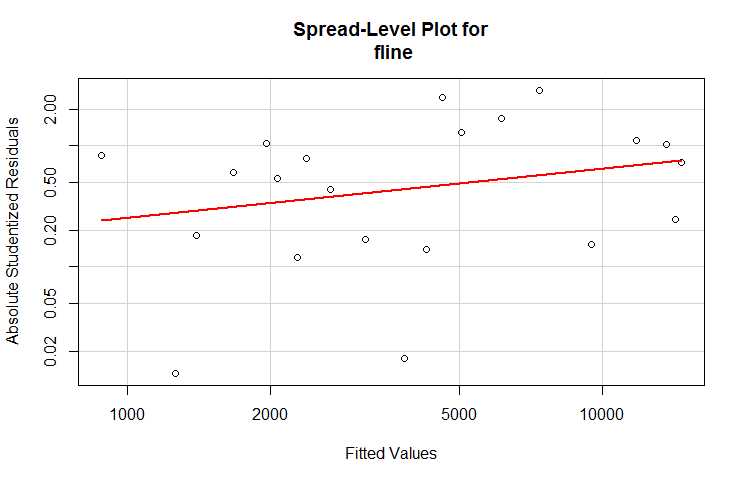
spreadLevelPlot
创建标准化残差绝对值与拟合值的散点图。
若输出结果建议幂次变换(suggested power transformation)接近1,则异方差不明显,即不需要进行变换;
若幂次变换为0.5,则用根号y代替y;
若幂次变换为0,则用对数变换。
> > spreadLevelPlot(fline) Suggested power transformation: 0.5969254 >
自相关性检验:
在线性回归模型基本假设中有 cov(εi ,εj)=0 的假设,如果一个模型不满足该式则称随机误差项之间存在自相关现象。
注意:这里的自相关不是指两个或两个以上的变量之间的相关关系,而是指一个变量前后期数值之间的相关关系。
原假设:随机误差之间存在相关性。 -------P值>0.05 拒绝原假设,即不存在自相关现象。
> > durbinWatsonTest(fline) lag Autocorrelation D-W Statistic p-value 1 0.3578255 1.25138 0 Alternative hypothesis: rho != 0 >
从结果可以看出 P<0.05 接受原假设,存在严重自相关性。
共线性检验:
vif
VIF:variance inflation factor 方差扩大因子
一般情况下,VIFi>10 就表明存在多重共线性问题;而方程的多重共线性就是由VIF>10的这几个变量引起的。
>
> fline1<-lm(y~x1+x2+x4,data=bank)
> vif(fline1)
x1 x2 x4
4.830666 91.196064 88.411675
>
> cor(bank[,c(2,3,5)])
x1 x2 x4
x1 1.0000000 0.8904046 0.8867331
x2 0.8904046 1.0000000 0.9943239
x4 0.8867331 0.9943239 1.0000000
>
> fline2<-lm(y~x1+x4,data=bank)
> vif(fline2)
x1 x4
4.67936 4.67936
>
从回归方程 fline1的结果可以看出 X2与X4的VIF值明显的大于10,说明这两个变量之间存在着共线性;
同时,从简单相关系数矩阵也可以看出X2与X4之间的相关系数为0.9943239,表明两者之间高度相关。
可以通过删除VIF最大的变量来消除多从共线性,在删除X2后回归方程 fline2的结果就不存在明显的多重共线性现象。
异常值检验:
异常值点分为两种情况:(1)关于因变量y异常;(2)关于自变量x异常
(1)离群点 :预测效果不佳的点,具有加大残差。
outlierTest
根据最大的残差值的显著性来判断是否存在离群点。
若不显著 Bonferonni P>0.05 ,表明没有离群点;
若显著 Bonferonni P<0.05 ,表明该最大残差值点为离群点,需要删去,然后对删除该点后的拟合模型再次进行离群点的检验。
>
> outlierTest(fline)
No Studentized residuals with Bonferonni p < 0.05
Largest |rstudent|:
rstudent unadjusted p-value Bonferonni p
16 -2.879438 0.011463 0.24071
>
(2)高杠杆点
距离样本总体较远的点,对回归参数影响加大。
杠杆值大于均值的2~3倍的样本点即可认为是高杠杆点。
>
> hatvalues(fline)
1 2 3 4 5 6 7
0.4453268 0.1937509 0.1943925 0.1376962 0.2137907 0.1647341 0.2542901
8 9 10 11 12 13 14
0.1114443 0.1203456 0.1075918 0.1372937 0.1113233 0.2690678 0.2546604
15 16 17 18 19 20 21
0.1712032 0.1200677 0.2205161 0.3279132 0.3918183 0.2912191 0.7615544
>
从各样本点的杠杆值可以看出 第21个样本点的杠杆值明显较大,为高杠杆点。
(3)强影响点
对模型的参数估计有较大的影响的点(综合考虑了残差和杠杆值),若将其删除则会导致模型发生本质的改变。
可以通过Cook距离来判断
> cooks.distance(fline)
1 2 3 4 5
1.146928e-01 8.816365e-06 1.721683e-03 1.180151e-02 5.950745e-02
6 7 8 9 10
1.188010e-02 1.049215e-03 1.595864e-02 5.529126e-03 7.215198e-04
11 12 13 14 15
1.040969e-05 5.131290e-04 3.465269e-01 1.077292e-01 1.045665e-01
16 17 18 19 20
1.554358e-01 1.388942e-03 1.154579e-01 1.330203e-01 5.371479e-03
21
3.517750e-01
>
第21个样本点的Cook值明显偏大,故具有较强的影响。
influence.measures
样本点有强影响则在右侧用 * 标记
>
> influence.measures(fline)
Influence measures of
lm(formula = y ~ x1 + x2 + x3 + x4, data = bank) :
dfb.1_ dfb.x1 dfb.x2 dfb.x3 dfb.x4 dffit cov.r cook.d hat inf
1 0.45826 -0.568459 0.055623 0.512937 0.009836 0.75016 1.981 1.15e-01 0.445 *
2 -0.00507 0.004561 -0.000964 0.000134 0.000275 -0.00643 1.713 8.82e-06 0.194
3 -0.06156 0.064613 -0.021146 -0.035703 0.013871 -0.08994 1.695 1.72e-03 0.194
4 -0.15306 0.124729 -0.077062 0.020415 0.062390 -0.23797 1.425 1.18e-02 0.138
5 -0.19112 0.045121 -0.136219 0.376396 0.126321 -0.54719 1.232 5.95e-02 0.214
6 -0.05657 -0.004141 -0.023041 0.165138 0.024055 -0.23824 1.503 1.19e-02 0.165
7 0.00462 0.013033 -0.013136 -0.058289 0.012084 0.07016 1.843 1.05e-03 0.254
8 -0.01447 -0.000661 -0.180381 0.032928 0.169471 0.27911 1.269 1.60e-02 0.111
9 -0.03729 0.017606 -0.096442 0.056441 0.084377 0.16202 1.473 5.53e-03 0.120
10 -0.02597 0.030394 -0.027975 -0.018465 0.020941 0.05821 1.533 7.22e-04 0.108
11 -0.00312 0.002135 -0.000075 0.004076 -0.000837 0.00699 1.600 1.04e-05 0.137
12 0.03346 -0.031808 0.013247 -0.004924 -0.005163 -0.04908 1.544 5.13e-04 0.111
13 -0.88710 1.114394 -0.618970 -0.968065 0.435245 1.51702 0.331 3.47e-01 0.269 *
14 -0.46471 0.322235 -0.157021 0.463529 0.054450 0.74845 1.103 1.08e-01 0.255
15 0.54324 -0.482824 -0.052544 -0.244757 0.172698 -0.76306 0.704 1.05e-01 0.171
16 0.76658 -0.744780 0.123881 -0.025557 0.011793 -1.06364 0.174 1.55e-01 0.120
17 0.01766 -0.010056 -0.043461 -0.040832 0.045946 -0.08075 1.758 1.39e-03 0.221
18 0.05049 0.055714 0.583416 -0.186662 -0.554400 0.76448 1.399 1.15e-01 0.328
19 0.20494 -0.110758 0.593949 -0.153020 -0.518155 0.81642 1.627 1.33e-01 0.392
20 -0.04819 0.059309 -0.002337 -0.027989 -0.022679 -0.15900 1.909 5.37e-03 0.291
21 -0.20629 0.281238 0.822119 0.113466 -0.986662 -1.30680 4.861 3.52e-01 0.762 *
>
>
从结果来看 第1,13,21 个样本点的影响较大。
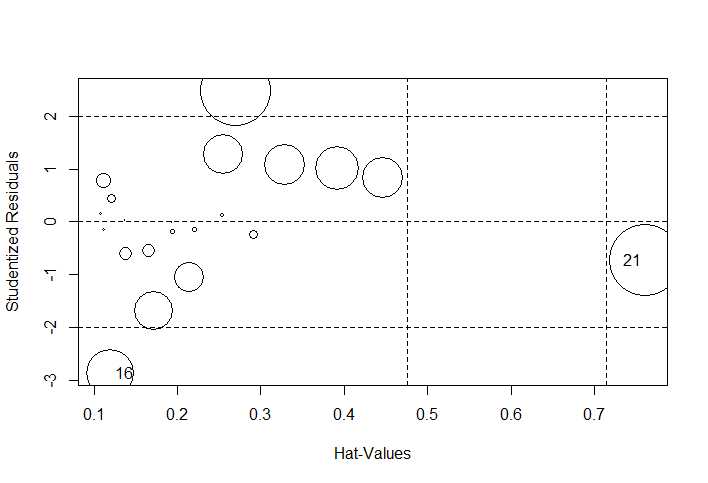
influencePlot
将离群点、高杠杆点、强影响点整合到一个图中。
纵坐标在 -2~2之外的可以认为是离群点;
横坐标为杠杆值;
圆圈大小代表影响值大小。
标签:
原文地址:http://www.cnblogs.com/runner-ljt/p/4583804.html