标签:
问题描述:字符串的左旋转操作定义为:把字符串前面n个字符移动到字符串的尾部;如取n=3,把字符串asdfghj左旋转3位得到字符串fghjasd。请实现字符串左旋转的函数,要求对长度为length的字符串操作的时间复杂度为O(length),空间复杂度为O(1)。
实现字符串左旋转很简单,但是有时间复杂度和空间复杂度的要求。
对于前面的n个字符串,每次左旋一位,整个字符串也紧跟着移动向左移动一位,以此循环,直至左旋n个字符串。
假设字符串char S[length+1],额外开辟一个字符串变量char b,S=‘asdfghj‘,length = 7,n=3,m=length-n=4。该方法的示意图如下:
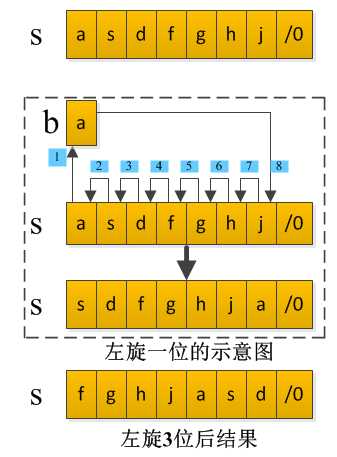
该算法思路简单明了,但是时间复杂度比较高,为n*m,代码如下:
void left_mov(char s[],int n)
{
int i,j;
char b;
for(i=0;i<n;i++)
{
b = s[0];
j = 0;
while(NULL != s[j+1])
{
s[j] = s[j+1];
j++;
}
s[j] = b;
}
cout<<s;
}
对此,引出一些别的方法,如指针翻转法、递归转换法(详情参考July的博客 http://blog.csdn.net/v_JULY_v/article/details/6322882)。指针反转法,递归转换法,这些方法,都没有把字符串S中的元素进行一步到位的移动,这就使得移动的次数很多。假如对于字符串S中的每个元素,能够计算出字符串左旋m位之后,每个元素的具体位置,那样就可以一次性的移动到该位置,这样子就可以大大降低时间复杂度了,针对这个思路,提出了以下算法:
int num 作为循环停止的一个判断条件,当num=length-1的时候停止循环;int k 表示执行每一步step之后,字符串中空出的元素的下标为k,即下一个step就要填补这第k个元素的位置;int m = length-n 表示剩余的m个要左移的元素(当然了,前面那n个元素要补在这m个元素的后面,要不怎么叫做左移),为了便于区别,我们这里做一下定义,S_n表示由字符串S的前面n个元素组成的一个子串(S[0-(n-1)]),S_m表示由字符串S的后面m个元素组成的一个子串(S[n-length])。
刚开始的时候,将S[0]转移给b,即S[0] -> b,此时,令k = 0; num = 0; 知道了k之后,怎么求出下一个k,这是一个比较难的问题,也是这个方法的核心。因为k是当前字符串空出的元素的下标,那么,这个位置应该放什么元素呢?当k=0的时候,那么,S[k]将要存放的肯定是S_m的第一个元素,为什么呢,因为S的前面的n个元素都要被左旋转到S的后面了,那么旋转后,S[0]存放的肯定就是S_m的第一个元素;同理可以知道,当k=1的时候,S[1]存放的肯定就是S_m的第二个元素......可是,问题又来了,当超过S_m的容量的时候怎么办呢,因此,得到k之后,要做一下判断,判断S[k]将要存放的是S_m中的元素还是S_n中的元素,如果是S_m中的,那存放的又是S_m中的哪一个元素,如果是S_n中的,存放的又是S_n中的哪一个元素;仔细推敲一下,就可以得到以下的结论:
if(k<m)
{
s[k] = s[lenth-(m-k)];
k = lenth-(m-k);
}
else
{
s[k] = s[n-(lenth-k)];
k = n-(lenth-k);
}
由此,我们可以得到如下图的基本思路,蓝的的数字表示相应的step;转移过程表示字符串中元素的转移,S[0] -> b表示将S[0]中的字符串存放在b中,同理S[3] -> S[0]表示将S[3]存放在S[0]中:num从零开始,字符串S中更新(存入替代原来的)一个元素,就自加1;k的转移过程根据上面的方法来进行判断;step 7 进行完毕之后,num=6,表示S中已经有6个字符串进行更新了,那么此时要结束循环,把存放在b中的那个元素放在S[k]中,这就是step 8。
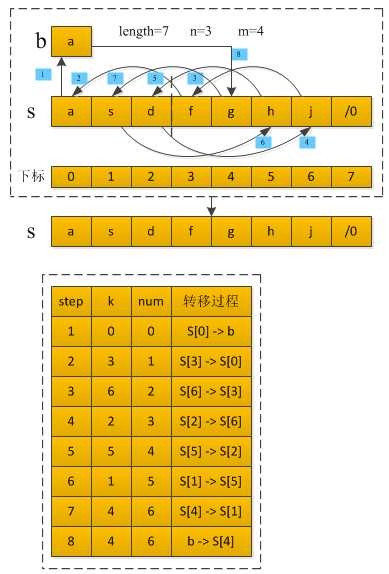
代码如下:
void left_mov1(char s[],int lenth, int n)
{
int k,m;
char b;
n = n%lenth;//当n>length的时候,取模
k = 0;
b = s[0];
m = lenth-n;
int num = 0;
k = 0;
while(num<(lenth-1))
{
if(k<lenth-n)
{
s[k] = s[lenth-(m-k)];
k = lenth-(m-k);
}
else
{
s[k] = s[n-(lenth-k)];
k = n-(lenth-k);
}
num++;
}
s[k] = b;
cout<<s;
}
算法分析:k的取值顺序为0->3->6->2->5->1->4,把S中所有的元素都遍历更新了一遍,时间复杂度为O(length),空间复杂度为O(1),而且只需要进行n+1次转移操作,与指针翻转法、递归转换法这些方法相比,有一定的优势。加入对于所有的长度为length的字符串,进行左旋n位操作之后,那么k是不是可以遍历完S中所有的元素呢?这个就需要进行验证了,为此,在此做了一下测试,输入length 和 n,输出k的遍历顺序:
void left1(int lenth, int n)
{
int k,m;
char b;
n = n%lenth;//当n>length的时候,取模
k = 0;
m = lenth-n;
int num = 0;
k = 0;
cout<<k<<" ";
while(num<(lenth-1))
{
if(k<lenth-n)
{
k = lenth-(m-k);
}
else
{
k = n-(lenth-k);
}
cout<<k<<" ";
num++;
}
cout<<endl;
}
int main()
{
int lenth,n;
cout<<"lenth=";
cin>>lenth;
cout<<"n=";
cin>>n;
cout<<"遍历的顺序依次为:"<<endl;
left1(lenth,n);
return 0;
}
一些测试如下:

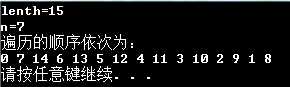
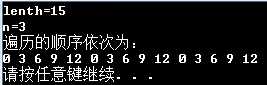
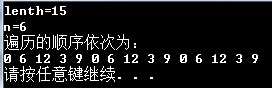
问题出现了,果然就像之前所说的那样,k不一定能够遍历完S中所有的元素,出现了循环。为此,又查看了July的博客(http://blog.csdn.net/v_JULY_v/article/details/6322882)。

第一个和第二个测试实验,可以遍历完所有的元素,对于第三个和第四个,不可以遍历完所有的元素,那是因为length和n的最大公约数不是1,它们两个不是互质的;为此,输入数据之后,要判断一下length和n的最大公约数gcd(length,n)。对于第三个测试实验,当n=3的时候,那么,猜测会出现3个环,因为0->3->6->9->12,这里只有五个元素,因此,还有两个这样子的环;为此,需要对算法进行改进,当回到原点的时候,要对k进行加1,目测这样子可以可以遍历完S中所有的元素。于是推出如下的改进方法:
int gcd(int m, int n)//返回值n是m和n的最大公约数
{
int r;
while(0 != m%n)
{
r = m%n;
m = n;
n = r;
}
return n;
}
void left3(int lenth, int n)
{
int k,m,num;
k = 0;
m = lenth-n;
n = n%lenth;
int gcd_n= gcd(lenth,n);
if(1 == gcd_n)
{
int k,m,num;
k = 0;
m = lenth-n;
num = 0;
cout<<k<<" ";
while(num<lenth-1)
{
if(k<m)
{
k = lenth - (m-k);
cout<<k<<" ";
}
else
{
k = n - (lenth-k);
cout<<k<<" ";
}
num++;
}
cout<<endl;
}
else
{
for(int kk=0;kk<gcd_n;kk++)
{
k = kk;
int num = 0;
cout<<kk<<" ";
while(num<(lenth/gcd_n-1))
{
if(k<m)
{
k = lenth-(m-k);
cout<<k<<" ";
}
else
{
k = n-(lenth-k);
cout<<k<<" ";
}
num++;
}
}
cout<<endl;
}
}
一些实验结果:
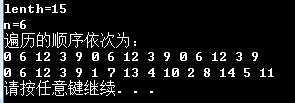

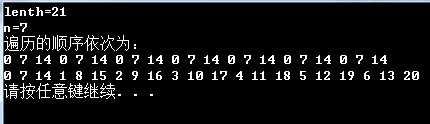

第一行的结果是上一个版本的,第二行的结果是改进之后的版本的,这次终于没有问题了;
最后,改进的左旋字符串代码如下:
int gcd(int m, int n)//返回值n是m和n的最大公约数
{
int r;
while(0 != m%n)
{
r = m%n;
m = n;
n = r;
}
return n;
}
void left_mov5(char s[],int lenth, int n)
{
int k,m;
char b;
n = n%lenth;//avoid that lenth < n
k = 0;
b = s[0];
m = lenth-n;
int gcd_n= gcd(lenth,n);
if(1 == gcd_n)
{
int num = 0;
k = 0;
while(num<(lenth-1))
{
if(k<m)
{
s[k] = s[lenth-(m-k)];
k = lenth-(m-k);
}
else
{
s[k] = s[n-(lenth-k)];
k = n-(lenth-k);
}
num++;
}
s[k] = b;
}
else
{
for(int kk=0;kk<gcd_n;kk++)
{
k = kk;
int num = 0;
b = s[k];
cout<<"b(";
cout<<kk<<")"<<" ";
while(num<(lenth/gcd_n-1))
{
if(k<m)
{
cout<<k<<"(";
s[k] = s[lenth-(m-k)];
k = lenth-(m-k);
cout<<k<<")"<<" ";
}
else
{
cout<<k<<"(";
s[k] = s[n-(lenth-k)];
k = n-(lenth-k);
cout<<k<<")"<<" ";
}
num++;
}
s[k] = b;
cout<<k<<"(b) ";
}
}
cout<<endl;
cout<<"The left_mov string a is :";
cout<<s;
}
int main()
{
const int Max = 100;
int n,lenth=0;
char a[40];
cout<<"Please input the string a :";
cin>>a;
while(NULL != a[lenth]) lenth++;
cout<<"The lenth of string a is : "<<lenth<<endl;;
cout<<"Please input the number n :";
cin>>n;
left_mov5(a,lenth,n);
cout<<endl;
return 0;
}
一些实验结果:
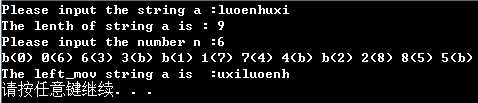


这次终于成功了,噢耶!

标签:
原文地址:http://www.cnblogs.com/luoenhu/p/4588461.html