阿申准备报名参加GT考试,准考证号为N位数X1X2....Xn(0<=Xi<=9),他不希望准考证号上出现不吉利的数字。他的不吉利数学A1A2...Am(0<=Ai<=9)有M位,不出现是指X1X2...Xn中没有恰好一段等于A1A2...Am. A1和X1可以为0
标签:
阿申准备报名参加GT考试,准考证号为N位数X1X2....Xn(0<=Xi<=9),他不希望准考证号上出现不吉利的数字。他的不吉利数学A1A2...Am(0<=Ai<=9)有M位,不出现是指X1X2...Xn中没有恰好一段等于A1A2...Am. A1和X1可以为0
第一行输入N,M,K.接下来一行输入M位的数。 100%数据N<=10^9,M<=20,K<=1000 40%数据N<=1000 10%数据N<=6
阿申想知道不出现不吉利数字的号码有多少种,输出模K取余的结果.
大意:求有多少n位的字符串 不包含给出的字符串
分析:n那么大,那肯定是矩阵乘法快速幂了。
可以用KMP,但自从AC自动机出现,KMP就成了时代的眼泪(#题外话)
所以我不会用KMP,所以我用了AC自动机
其实无论是一个限制串还是多个限制串(前提是总字符数量不要太多),原理都是一样的
下面介绍一下AC自动机
(我的介绍比较简略,如果看还是结合别人的介绍比较好)
1 2 3 4 5 6 7 8 9 10 11
原始串 A : a b c d a b c d a b d
要寻找的串 B :a b c d a b d
比如我们现在匹配,比如第 7 位不同,我们肯定不会从B串的第一位从新开始寻找,而是从第3位开始匹配,因为第 1 - 2 个字符与第5 - 6个字符相同(都是a b ),所以与KMP类似,我们在建设AC自动机时,要对每一位(假设第 x 位)的字符都找一个点,使得第 1 - i 位的字符与 第 x - i + 1 - x位的字符相同,并是的这样的与开头一段相同的串最长(即 i 最大),这样来解决匹配失败的问题,这个东西我们用Next 来记录(即匹配失败后,从哪一位开始匹配),而AC自动机就是在字母树的基础上添加Next的用法,如图所示。
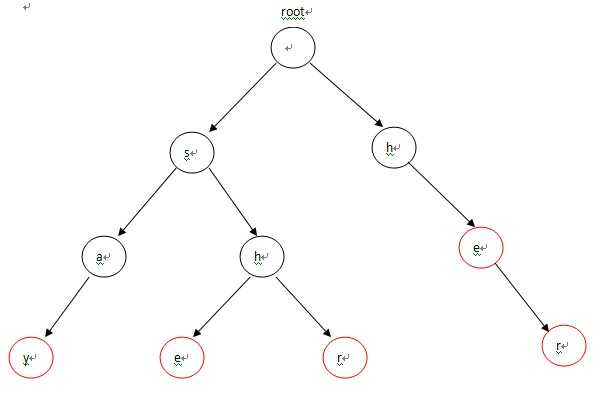
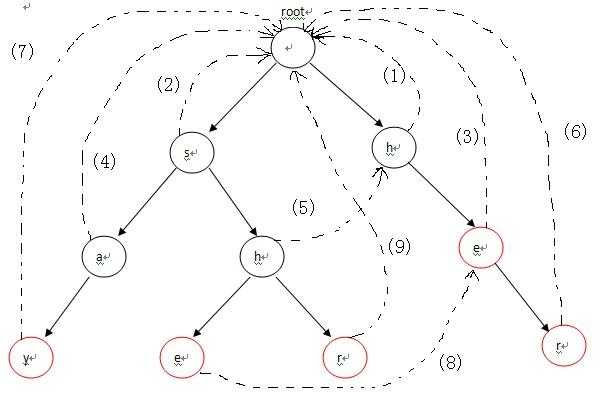
(图片来源:http://blog.csdn.net/niushuai666/article/details/7002823)
我手工不好,不会画图,囧
那在AC自动机中如何求Next,很简单,我们先不考虑根节点和最开始的几个节点的next指向哪里,对于第x个节点,他的父亲节点为第 fa 个节点,这个节点字符 CHAR, 为假设第fa个节点以及fa节点以上的部分都求好了Next,那么根据Next定义,我们只要不断的对第 fa 位求Next,求了之后再求(即 fa = Next(fa), fa = Next(fa) ),直到找到一个Next,这个Next节点有对应的孩子,那么Next[x] = Child[ fa (不断求Next之后的)][ CHAR ]
如果考虑根节点和最开始的几个节点,那就相当于初始化罢了,初始节点以及初始节点的孩子(相当于限制串的第一个点)的Next都指向起始节点
1 2 3 4 5 6 7 8 9 10 11 12 13 14
a b a b a b c a b a b a b c
比如已经求得
Next 1 2 3 4 5 6 7 8 9 10 11 12 13 14
0 0 1 2 3 4 0 1 2 3 4 5 6 ?
求第14位时那就对第13位求Next, fa=>6,第6位后面有字母c了,那么 Next[14]就是 7
相同的在字母树上,相当于每一位的字符后面接着多个字符罢了。。。
讲完AC自动机就讲讲怎么用矩阵加速:
设AC自动机有Tot个节点,所求字符串共N位(即题面中准考证的位数),
若求准考证的种数,相当于求在AC自动机中从起始位置开始走N步,不碰到危险节点,有多少种走法
F[ k ].M[ i ][ j ] 表示用 k 步从第 i 个节点走到 第 j 个节点
显然从 k 到 k+1的转移是固定的,所以可以用矩阵乘法快速幂优化
综上所述,本题得解

1 #include <cstdio> 2 #include <cstring> 3 #include <cstdlib> 4 #include <cmath> 5 #include <deque> 6 #include <vector> 7 #include <queue> 8 #include <iostream> 9 #include <algorithm> 10 #include <map> 11 #include <set> 12 #include <ctime> 13 using namespace std; 14 typedef long long LL; 15 typedef double DB; 16 #define For(i, s, t) for(int i = (s); i <= (t); i++) 17 #define Ford(i, s, t) for(int i = (s); i >= (t); i--) 18 #define MIT (2147483647) 19 #define INF (1000000001) 20 #define MLL (1000000000000000001LL) 21 #define sz(x) ((int) (x).size()) 22 #define clr(x, y) memset(x, y, sizeof(x)) 23 #define puf push_front 24 #define pub push_back 25 #define pof pop_front 26 #define pob pop_back 27 #define ft first 28 #define sd second 29 #define mk make_pair 30 inline void SetIO(string Name) { 31 string Input = Name+".in", 32 Output = Name+".out"; 33 freopen(Input.c_str(), "r", stdin), 34 freopen(Output.c_str(), "w", stdout); 35 } 36 37 const int N = 30, M = 20; 38 int n, m, Mod; 39 int Tot; 40 struct Matrix { 41 int M[N][N]; 42 43 Matrix() { 44 clr(M, 0); 45 } 46 47 inline Matrix operator *(Matrix &A) { 48 Matrix Ret; 49 For(i, 0, Tot) 50 For(j, 0, Tot) 51 For(k, 0, Tot) { 52 Ret.M[i][j] += M[i][k]*A.M[k][j]; 53 Ret.M[i][j] %= Mod; 54 } 55 return Ret; 56 } 57 } Transfer; 58 struct Node { 59 int Child[M], Next; 60 bool Danger; 61 #define Child(x, y) Tr[x].Child[y] 62 #define Next(x) Tr[x].Next 63 #define Danger(x) Tr[x].Danger 64 } Tr[N]; 65 string S; 66 queue<int> Que; 67 68 inline void Input() { 69 scanf("%d%d%d", &n, &m, &Mod); 70 cin>>S; 71 } 72 73 inline int Find(int x, int y) { 74 while(x && !Child(x, y)) x = Next(x); 75 return Child(x, y); 76 } 77 78 inline void Build() { 79 int Now = 0; 80 For(i, 0, m-1) { 81 int x = S[i]-‘0‘; 82 Child(Now, x) = ++Tot; 83 Danger(Tot) = 0; 84 Now = Tot; 85 } 86 Danger(Tot) = 1; 87 88 Next(0) = 0; 89 For(i, 0, 9) Next(Child(0, i)) = 0; 90 For(i, 0, 9) 91 if(Child(0, i)) Que.push(Child(0, i)); 92 while(sz(Que)) { 93 int x = Que.front(); 94 Que.pop(); 95 for(int Tab = Next(x); Tab && !Danger(x); Tab = Next(Tab)) 96 Danger(x) |= Danger(Tab); 97 98 For(i, 0, 9) 99 if(Child(x, i)) Que.push(Child(x, i)); 100 101 For(i, 0, 9) 102 if(Child(x, i)) Next(Child(x, i)) = Find(Next(x), i); 103 else Child(x, i) = Find(Next(x), i); 104 } 105 106 For(i, 0, Tot) { 107 if(Danger(i)) continue; 108 For(j, 0, 9) { 109 if(Danger(Child(i, j))) continue; 110 Transfer.M[i][Child(i, j)]++; 111 } 112 } 113 } 114 115 inline Matrix Power(Matrix &Basic, int Tim) { 116 Matrix Ret; 117 For(i, 0, Tot) Ret.M[i][i] = 1; 118 while(Tim) { 119 if(Tim&1) Ret = Ret*Basic; 120 Basic = Basic*Basic, Tim >>= 1; 121 } 122 return Ret; 123 } 124 125 inline void Solve() { 126 Build(); 127 128 Matrix Ret; 129 Ret = Power(Transfer, n); 130 131 int Ans = 0; 132 For(i, 0, Tot) 133 if(!Danger(i)) Ans += Ret.M[0][i]; 134 Ans %= Mod; 135 136 printf("%d\n", Ans); 137 } 138 139 int main() { 140 SetIO("1009"); 141 Input(); 142 Solve(); 143 return 0; 144 }
题外话:
为什么说KMP是时代的眼泪了呢?
其实这样说是不太准确的,KMP还是可以求最长重复子串的(子串之间不允许重叠),其他问题可以用其他方法解决
如果求最长重复子串(子串之间允许重叠),则用后缀数组,
至于其他,则大多可以用AC自动机代替
(当然,还有少数功能这里没有提到)
而后缀数组、AC自动机属于必学,且变化形式较少,代码较模版化,思考较简单,
KMP则有时需要大神的思维以及一点点小火花,
所以KMP还是不用专精,略学即可
(其实AC自动机跟KMP原理是一样的,我只不过实在胡说八道罢了)
标签:
原文地址:http://www.cnblogs.com/StupidBoy/p/4590489.html