拉格朗日对偶性

标签：

　　主要解决带约束的最优化问题，把原始问题转换为对偶问题，在支持向量机中有使用

　　f(x),c_i(x),h_j(x)是Rⁿ(n维实数集)上的连续可微函数

　　1.原始问题：

　　　　目标函数：min f(x)   (x∈Rⁿ)                       

　　　　约束条件：c_i(x)≤0    (i=1,2...k)

　　　　　　　　　h_j(x)=0    (j=1,2...l)              ps:这种写法和拉格朗日乘法很相似

　　　　引进拉格朗日函数：

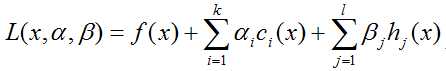
　　　　x为n维向量,α_i(α_i≥0)和β_j为拉格朗日乘子,定义关于x的函数如下：

　　　　假设存在x违反约束条件，即存在某个i使得c_i(w)>0或者某个j使得h_j(w)≠0，令对应i的α_i→+∞，令对应j的β_jh_j(x)→+∞,其余的α和β项全为0，则Θ_P(x)→+∞

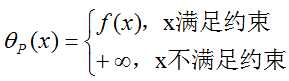
　　　　则目标函数

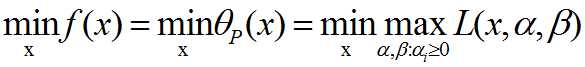
　　　　　　　　　 ps：广义拉格朗日的极小极大问题

　　　　定义如下p^*为原始问题的值

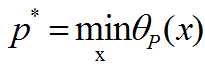
　　2.对偶问题：

　　　　定义如下公式

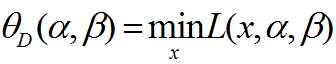
　　　　对其进行极大化

　　　　　　　　　 ps：广义拉格朗日的极大极小问题

　　　　则定义原始问题的对偶问题，d^*为对偶问题的值

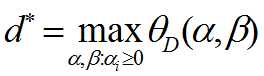
　　3.原始问题与对偶问题的关系：

　　　　1.若原始问题和对偶问题均有最优值，则d^*≤p^*

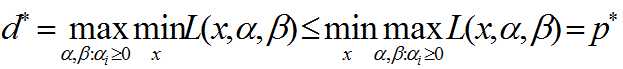
　　　　2.设x^*,α^*,β^*分别为原始问题和对偶问题的可行解且d^*=p^*，则x^*,α^*,β^*分别为原始问题和对偶问题的最优解

　　　　3.假设f(x)和c_i(x)是凸函数，h_j(x)是仿射函数，并且不等式约束c_i(x)严格执行

　　　　　则x^*,α^*,β^*分别为原始问题和对偶问题的解的充要条件是x^*,α^*,β^*满足KKT条件

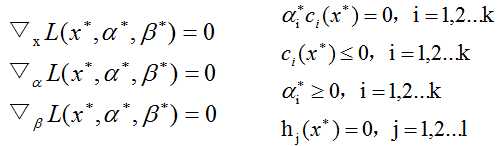
　　　　　ps:整理这些东西真没把我累个半死，公式太多了，可是我有强迫症，全都重新写了一遍，参考《统计学习方法》

拉格朗日对偶性

标签：

原文地址：http://www.cnblogs.com/smallby/p/4594379.html