标签:
图的定义
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成。注意:在图结构中,不允许没有顶点,在定义中,如果V是顶点的集合,则强调了顶点集合V的有穷非空。
在图中,若不存在顶点到其自身的边,且同一条边不重复出现,则称这样的图为简单图。
图的存储结构
邻接矩阵
考虑到图是由顶点和边或者弧两部分组成的。合在一起比较困难,那就自然地考虑到分两个结构来分别存储。顶点不分大小、主次,所以用一个一位数组来存储是很不错的选择。而边或者弧是顶点与顶点之间的关系,一维搞不定,那就考虑用一个二维数组来存储。

对于带权值的图,可以令不可达的边的权值为无穷大。利用这个无穷大代表两个顶点不可达。
邻接矩阵结构代码
//为了简单,默认顶点为int类型,也就是v0,v1,v2等的那个下标
//权值为int类型
#define MAXVEX 100
#define INF 65535
typedef struct
{
int vexs[MAXVEX];
int arc[MAXVEX][MAXVEX];
int numVertexes, numEdges;
}MGraph;
无向图的创建代码:
void CreateMGraph(MGraph *G)
{
//k为循环变量
int k = 0;
//i,j代表顶点的下标
int i = 0;
int j = 0;
printf("读取顶点和边的数目...\n");
scanf("%d,%d", &G->numVertexes, &G->numEdges);
//输入顶点信息
printf("读取顶点信息...\n");
for(k = 0; k < G->numVertexes; k++)
{
scanf("%d", &G->vexs[k]);
}
//初始化所有的边为无穷大
for(i = 0; i < G->numVertexes; i++)
{
for(j = 0; j < G->numVertexes; j++)
{
G->arc[i][j] = INF;
}
}//for
int weight = 0;
//获取权值的输入值
printf("读取边(vi,vj)中两个顶点的下表i、j和对应的权值...\n");
for(k = 0; k < G->numEdges; k++)
{
scanf("%d,%d,%d", &i, &j, &weight);
G->arc[i][j] = weight;
G->arc[j][i] = weight;
}//for
}//CreateMGraph()
无向图的边的二维数组是一个对称矩阵,有向图的创建更加简单。
测试代码:
void main(void)
{
freopen("in.txt", "r", stdin);
MGraph mGraph;
MGraph *pMGraph = &mGraph;
CreateMGraph(pMGraph);
fclose(stdin);
return;
}
试验数据:
//in.txt 4,5 0 1 2 3 0,1,10 0,2,2 0,3,7 1,2,8 2,3,5
邻接表
回忆在树的存储结构中,降到了一种孩子表示法,将这种数组与链表相结合的存储方法称为邻接表。
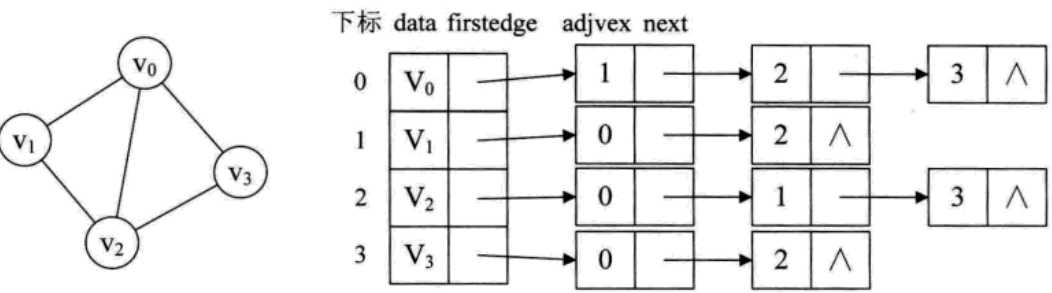
注意上图的数组称为顶点表,链表为边表结点。
对于有向图,其实更加简单,但是有向图的每一个顶点分为入度和出度。
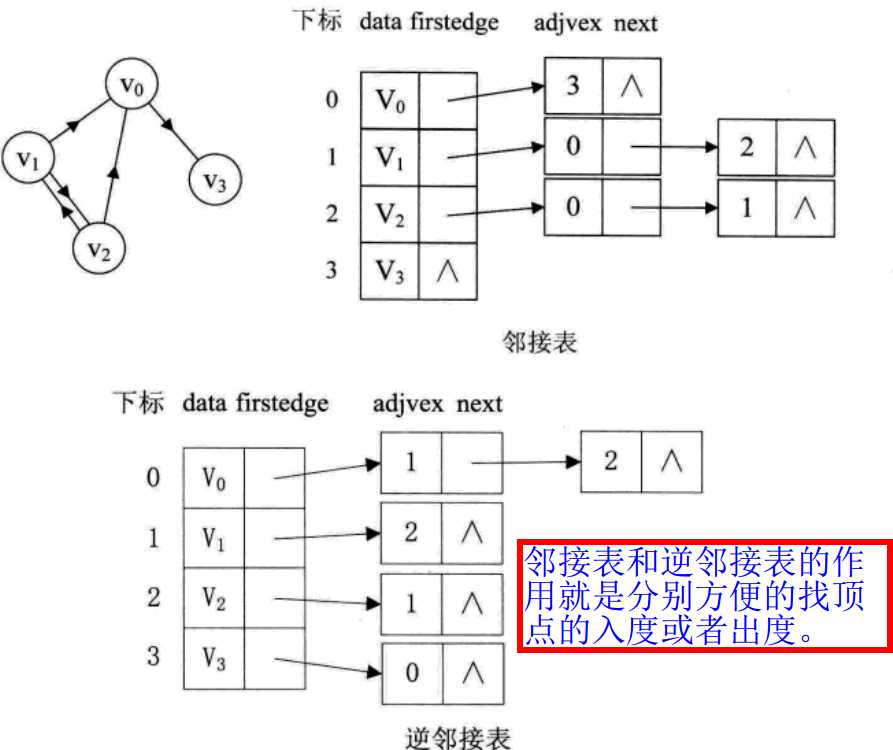
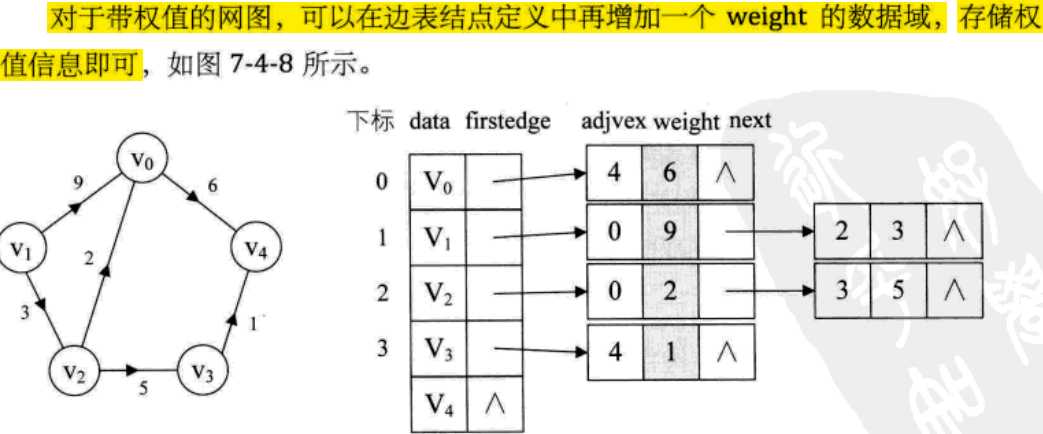
邻接表结构代码:
#define MAXVEX 100
typedef struct EdgeNode
{
int adjvex;
int weight;//边的权重,用int表示
struct EdgeNode *next;
}EdgeNode;
typedef struct VertexNode
{
int data;
EdgeNode *firstEdge;
}AdjList;
typedef struct
{
AdjList adjList[MAXVEX];
int numVertexs;
int numEdges;
}AdjGraph;
邻接表创建有向图代码:
void CreateAdjGraph(AdjGraph *G)
{
//统一规定,k用作循环变量
int k = 0;
printf("读取顶点和边数目...\n");
scanf("%d%d", &G->numVertexs, &G->numEdges);
printf("读取顶点...\n");
for(k = 0; k < G->numVertexs; k++)
{
scanf("%d", &G->adjList[k].data);
G->adjList[k].firstEdge = NULL;
}
printf("读取边信息...\n");
//i,j用作表示顶点的下表,weight表示边的权重
int i = 0;
int j = 0;
int weight = 0;
for(k = 0; k < G->numEdges; k++)
{
scanf("%d%d%d", &i, &j, &weight);
EdgeNode *pEdgeNode = (EdgeNode*)malloc(sizeof(EdgeNode));
pEdgeNode->adjvex = j;
pEdgeNode->weight = weight;
pEdgeNode->next = NULL;
//采用头插法,将这个边节点插入
pEdgeNode->next = G->adjList[i].firstEdge;
G->adjList[i].firstEdge = pEdgeNode;
/*无向图插入边信息
//对于无向图,这里要再次插入
EdgeNode *pEdgeNode = (EdgeNode*)malloc(sizeof(EdgeNode));
pEdgeNode->adjvex = i;
pEdgeNode->weight = weight;
pEdgeNode->next = NULL;
//采用头插法,将这个边节点插入
pEdgeNode->next = G->adjList[j].firstEdge;
G->adjList[j].firstEdge = pEdgeNode;
*/
}
}//CreateAdjGraph
在插入边表结点的时候,采用头插法更加简单一些。
测试代码:
void main(void)
{
freopen("in.txt", "r", stdin);
AdjGraph adjGraph;
AdjGraph *pAdjGraph = &adjGraph;
CreateAdjGraph(pAdjGraph);
fclose(stdin);
}
测试数据:
//in.txt 10 19 0 1 2 3 4 5 6 7 8 9 0 1 4 0 2 1 0 3 3 2 3 1 1 4 9 1 5 8 2 4 6 2 5 7 2 6 8 3 5 4 3 6 7 4 7 5 4 8 6 5 7 8 5 8 6 6 7 6 6 8 5 7 9 7 8 9 3
标签:
原文地址:http://www.cnblogs.com/stemon/p/4596128.html