标签:
这一节开始讲基础的Linear Regression算法。
(1)Linear Regression的假设空间变成了实数域
(2)Linear Regression的目标是找到使得残差更小的分割线(超平面)
下面进入核心环节:Linear Regression的优化目标是minimize Ein(W)

为了表达简便,首先需要把这种带Σ符号的转换成matrix form,如下:

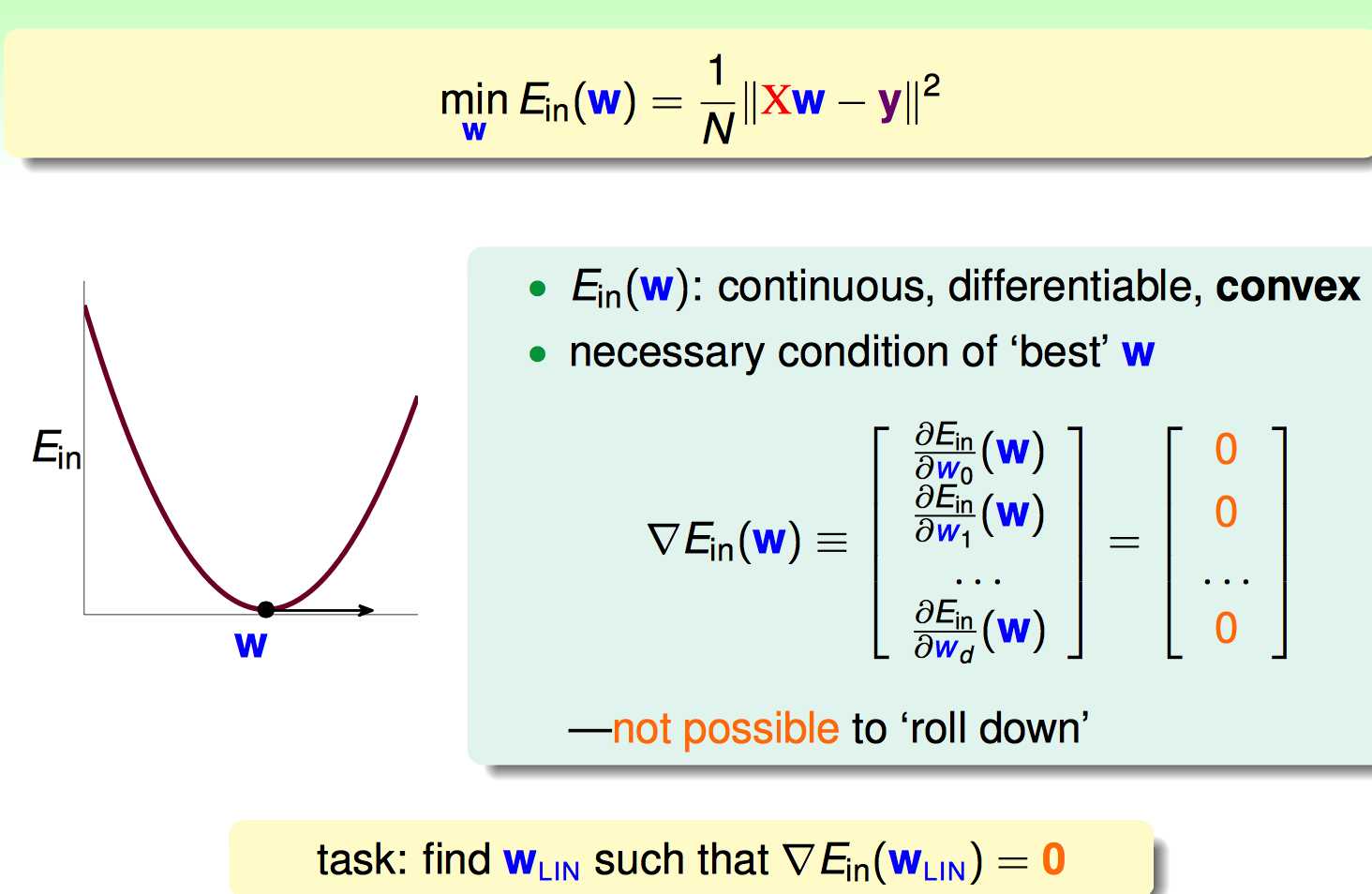
1~2:多个项的平方和可以转换成向量的平方
2~3:把每个列向量x都横过来,组成一个新的X矩阵
最后转换成了最终的minimize的表达式:连续可导,凸集,求梯度为0的点。求梯为0的过程如下:
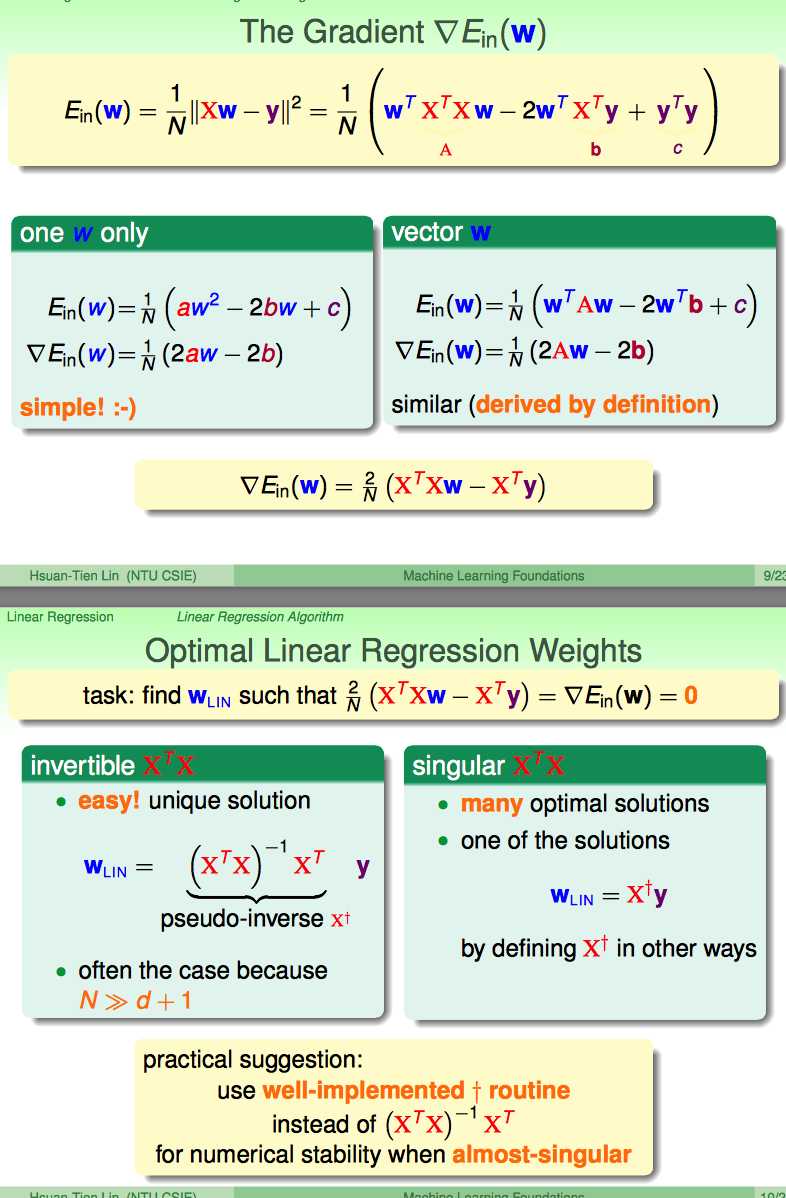
如何求出微分等于0的表达式。
第一张的式子设计到一些矩阵微分的公式,找到了下面这blog(http://blog.sciencenet.cn/blog-849193-653656.html)复习一下。
其中涉及到了二次函数的微分(Quadratic Products):注意,因为这里A=X‘X是对称阵,所以A==A‘,因此得到了2Aw

还涉及到了一次函数的微分(Linear Products)
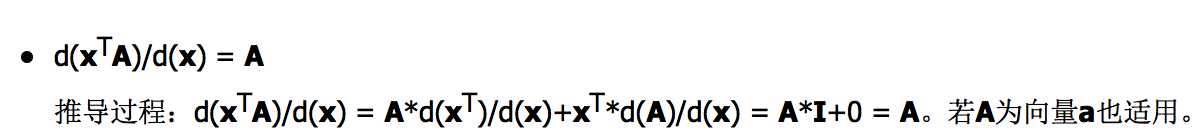
如何求出最终的结果。
这里分两种情况
(1)一种是X‘X是invertible的,显然直接求逆矩阵即可
(2)一种X’X是singluar的,这时应该求出广义逆矩阵
啥是广义逆?之前用ELM的时候学过一些。看课件再复习一下:

同时,林也推荐实际中用well-implemented routine 广义逆就好了。
因此,把广义逆矩阵算出来了,也就算OK了。
把求得的w带回去求得的矩阵拟合y^是XX(广义逆)y
这里又提炼出来一个Hat Matrix的概念:

课程中主要从几何意义的角度来阐述了这个hat matrix H是干啥的。
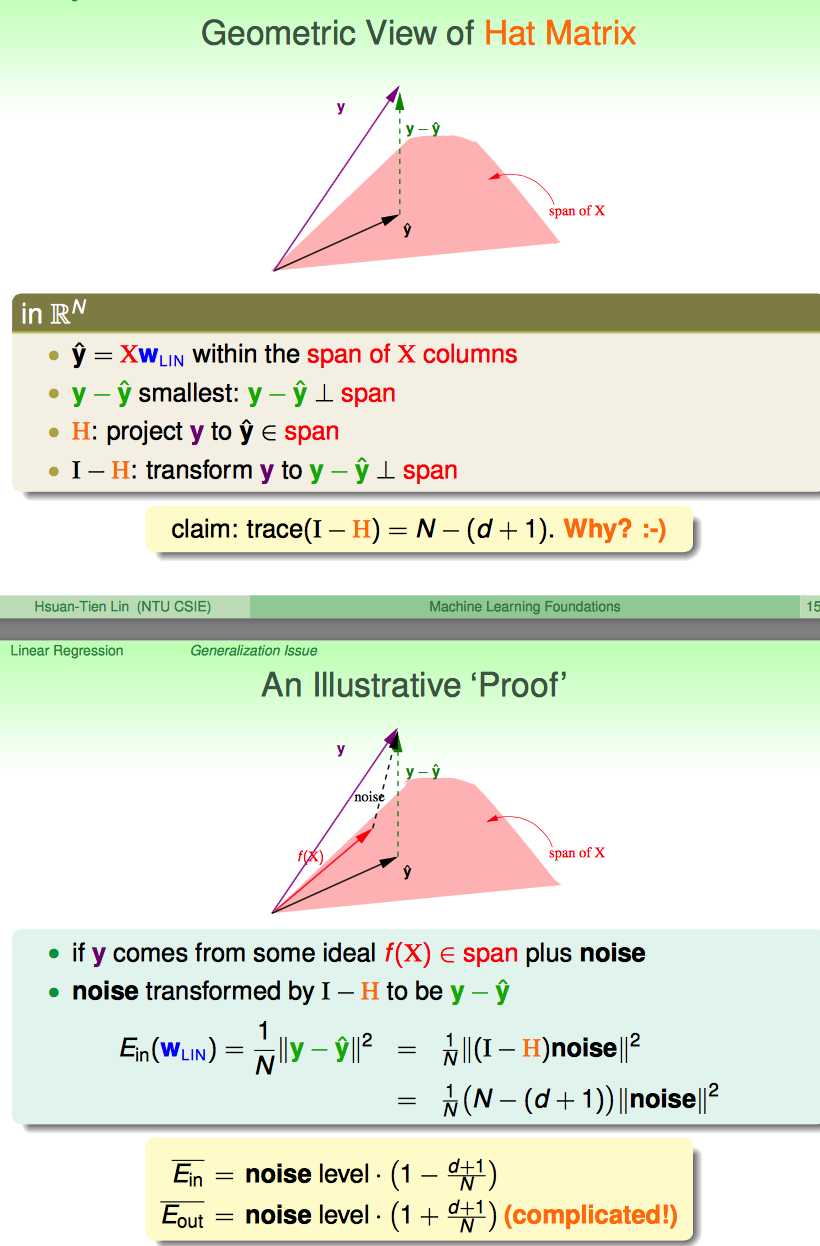
一开始理解这个gemoetric意义一直没有理解好,直到看了这篇blog(http://beader.me/mlnotebook/section3/linear-regression.html)之后,有些明白了。
大概是说,y hat是y到span of X的投影,这样一来,||y-yhat||²最小(垂线距离最短)。
这样看来,I-H这个线性变化就是把y变成了y-yhat。
换一个角度,可以把y看成是一个理想的f(x)+noise构成的;这样,其实也是是吧I-H这个线性变换应用在了nosie上面,变成了y-yhat。
换这个角度看有啥用呢?主要是为了得到Ein跟noise的关系
Linear Regression相当于把noise在原来基础上降低了1-(1+d)/N这么多。
但Eout却是比原来的noise大了。总结来说,见下图:
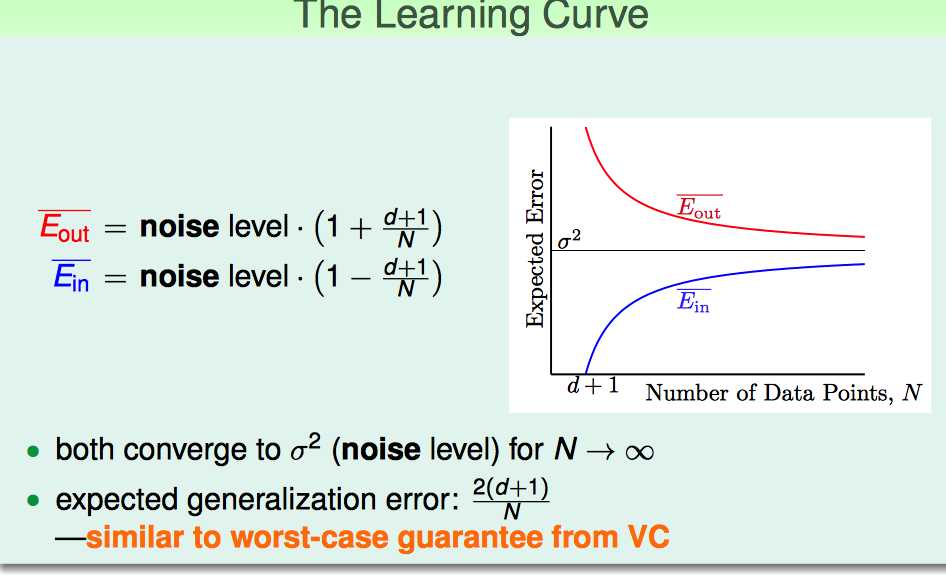
当N比较大时,Ein和Eout平均误差为2(d+1)/N级别的noise。
VC是Bound住错误的概率,但上面的Learning Curve说的是平均的情况,但是二者想表达的意思是相近的,就是N越大,Ein跟Eout越接近。
最后,又提到了一个问题Linear Classification vs. Linear Regression二者的关系。

我的理解有两点:
(1)直观看来,Regression似乎可以用来替代的Classification(因为毕竟只是少了一个算sign的步骤);而且classification是NP-hard的(算的慢),但是Linear Regression是analytic solution的(算得快)。
(2)对于classification的问题,y只有1和-1,把这两种情况下的Error曲线画出来,发现其实classification的线是一直在regression的线的下面的。
因此,结论就是,Linear Regression在Binary Classification问题上,是可以作为一个稍微宽松的错误上界的。

这里的trade-off的对象是算法的效率与error bound的紧密程度。
这里,林提出了一个practical的方法:实际中甚至可以先做一个regression来求一个初始化参数值,然后再应用诸如PLA/Pocket这类的算法降低error。
标签:
原文地址:http://www.cnblogs.com/xbf9xbf/p/4598600.html