HashMap实现分析

标签：

　　HashMap最基本的实现思想如下图所示，使用数组加链表的组合形式来完成数据的存储。

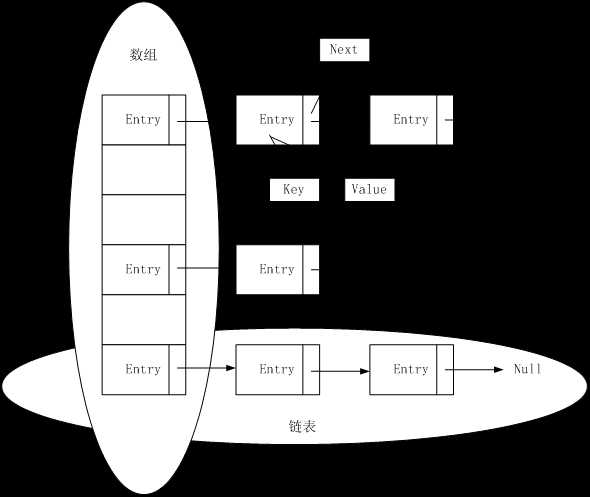
　　Entry在数组中的位置是由key的hashcode决定的。

　　向一个数组长度为16，负载因子为0.75的HashMap中插入key的hashcode为26、126、1、337、184、12、31、111的对象后的结构为：

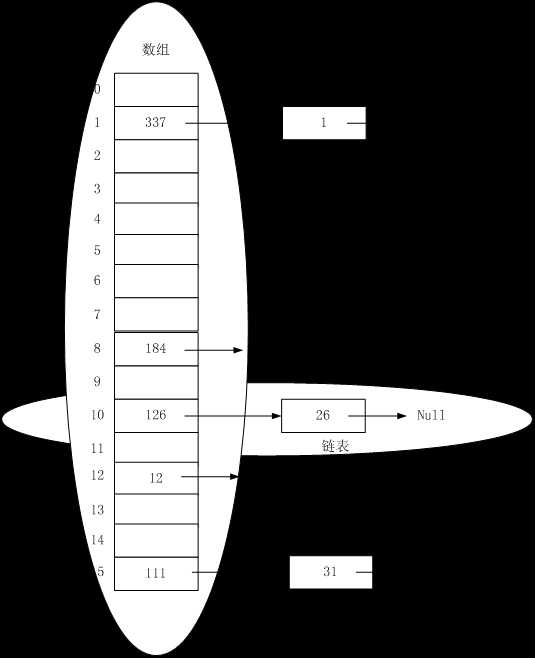
　　1%16 =1 ，337%16 =1。数组中存储的是最后插入的数据，并用next指针指向之前已经存在的数据。

　　HashMap查找数据的依据是：现根据key的hashcode查找位于数组中的位置，在使用next依次遍历链表中的元素，调用key的equals方法，如果key equals Entry对应的key，则Entry中的value就是所找的值。所以使用对象作为HashMap的key时，重写hashcode方法的同时需要重写equals方法。

　　可以参考HashMap的get方法的代码，就会更清楚上面的描述：

public V get(Object key) {
        if (key == null)
            return getForNullKey();
        int hash = hash(key.hashCode());
        for (Entry<K,V> e = table[indexFor(hash, table.length)];
             e != null;
             e = e.next) {
            Object k;
            if (e.hash == hash && ((k = e.key) == key || key.equals(k)))
                return e.value;
        }
        return null;
    }

　　HashMap中的Hash算法是经过了优化之后的，可以看到

　　int hash = hash(key.hashCode());对hashcode又进行了二次散列操作，这样做的目的是使得计算出的hash比hashcode在数组上的分布将更为均匀，HashMap的空间利用率也越高。

　　HashMap对hashcode的二次散列如下：　

static int hash(int h) {
        h ^= (h >>> 20) ^ (h >>> 12);
        return h ^ (h >>> 7) ^ (h >>> 4);
    }

　　HashMap在使用hash计算位于数组中的位置时也不是简单的%操作，而是用的indexFor来完成的。%操作比较耗资源，当HashMap中数组的length是2 的n次方时，h& (length-1)运算等价于h%length，但是&比%具有更高的效率。

static int indexFor(int h, int length) {
        return h & (length-1);
    }

　　理解了二次散列和indexFor，上面的代码就比较的好理解了。table数组就是图中的Entry数组。

　　HashMap可以存储key为null的Entry，该Entry将被放在数组指标为0的位置。

　　当HashMap中的元素越来越多的时候，hash冲突的几率也就越来越高，因为数组的长度是固定的。所以为了提高查询的效率，就要对HashMap的数组进行扩容，数组扩容这个操作也会出现在ArrayList中。最消耗性能的点就出现了：原数组中的数据必须重新计算其在新数组中的位置，并放进去，这就是resize。　

　　那么HashMap什么时候进行扩容呢？当HashMap中的元素个数超过数组大小*loadFactor时，就会进行数组扩容，loadFactor的默认值为0.75，这是一个折中的取值。也就是说，默认情况下，数组大小为16，那么当HashMap中元素个数超过16*0.75=12的时候，就把数组的大小扩展为 2*16=32，即扩大一倍，然后重新计算每个元素在数组中的位置，而这是一个非常消耗性能的操作，所以如果我们已经预知HashMap中元素的个数，那么预设元素的个数能够有效的提高HashMap的性能。

　　HashMap不是线程安全的，因此如果在使用迭代器的过程中有其他线程修改了map，那么将抛出ConcurrentModificationException，这就是所谓fail-fast策略。

　　这一策略在源码中的实现是通过modCount域，modCount顾名思义就是修改次数，对HashMap内容的修改都将增加这个值，那么在迭代器初始化过程中会将这个值赋给迭代器的expectedModCount。

　　在迭代过程中，判断modCount跟expectedModCount是否相等，如果不相等就表示已经有其他线程修改了Map：

　　modCount的修饰符为volatile，保证线程之间修改的可见性。

　　HashSet的底层也是用HashMap来实现的，使用HashMap的key来进行存储与散列。

HashMap实现分析

标签：

原文地址：http://www.cnblogs.com/lnlvinso/p/4601105.html