标签:
Redis:https://github.com/zwjlpeng/Redis_Deep_Read
本篇博文紧随上篇Redis有序集内部实现原理分析,在这篇博文里凡出现源码的地方均以下述src/version.h中定义的Redis版本为主
#define REDIS_VERSION "2.9.11"
在上篇博文Redis有序集内部实现原理分析中,我分析了Redis从什么时候开始支持有序集、跳表的原理、跳表的结构、跳表的查找/插入/删除的实现,理解了跳表的基本结构,理解Redis中有序集的实现就不难了,因为Redis有序集的实现也是以跳表作为基础的底层数据结构,选择这种数据结构,不仅仅是因为简单,更多的是因为性能。
Redis中跳表的基本数据结构定义如下,与基本跳表数据结构相比,在Redis中实现的跳表其特点是不仅有前向指针,也存在后向指针,而且在前向指针的结构中存在span跨度字段,这个跨度字段的出现有助于快速计算元素在整个集合中的排名
//定义跳表的基本数据节点 typedef struct zskiplistNode { robj *obj; // zset value double score;// zset score struct zskiplistNode *backward;//后向指针 struct zskiplistLevel {//前向指针 struct zskiplistNode *forward; unsigned int span; } level[]; } zskiplistNode; typedef struct zskiplist { struct zskiplistNode *header, *tail; unsigned long length; int level; } zskiplist; //有序集数据结构 typedef struct zset { dict *dict;//字典存放value,以value为key zskiplist *zsl; } zset;
将如上数据结构转化成更形式化的图形表示,如下图所示
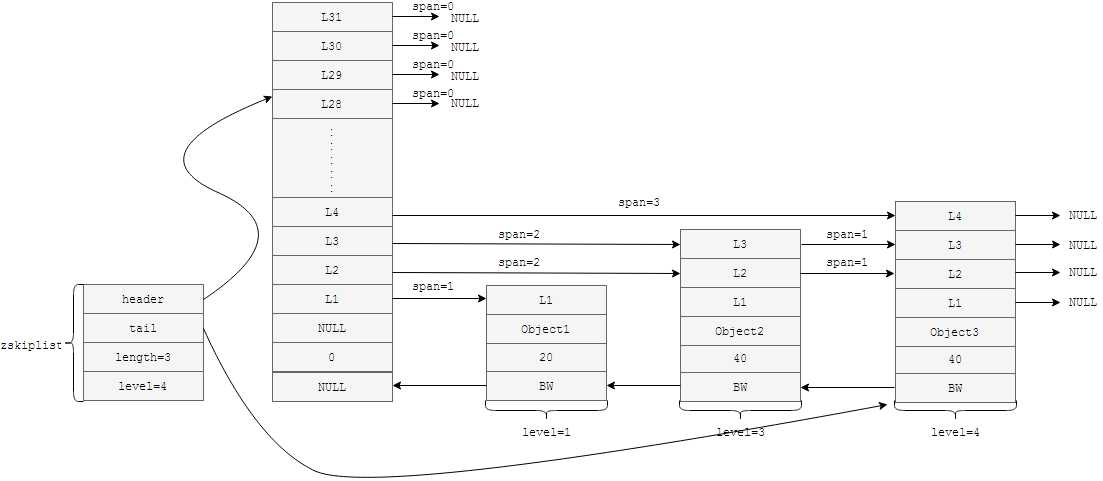
在上图中,可以看到header指针指向的是一个具有固定层级(32层)的表头节点,为什么定义成32,是因为定义成32层理论上对于2^32-1个元素的查询最优,而2^32=4294967296个元素,对于绝大多数的应用来说,已经足够了,所以就定义成了32层,到于为什么查询最优,你可以将其想像成一个32层的完全二叉排序树,算算这个树中节点的数量
Redis中有序集另一个值得注意的地方就是当Score相同的时候,是如何存储的,当集合中两个值的Score相同,这时在跳表中存储会比较这两个值,对这两个值按字典排序存储在跳表结构中
有了上述的数据结构相关的基础知识,来看看Redis对zskiplist/zskiplistNode的相关操作,源码如下所示(源码均出自t_zset.c)
创建跳表结构的源码
//#define ZSKIPLIST_MAXLEVEL 32 /* Should be enough for 2^32 elements */ zskiplist *zslCreate(void) { int j; zskiplist *zsl; //分配内存 zsl = zmalloc(sizeof(*zsl)); zsl->level = 1;//默认层级为1 zsl->length = 0;//跳表长度设置为0 zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL); for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) { //因为没有任何元素,将表头节点的前向指针均设置为0 zsl->header->level[j].forward = NULL; //将表头节点前向指针结构中的跨度字段均设为0 zsl->header->level[j].span = 0; } //表头后向指针设置成0 zsl->header->backward = NULL; //表尾节点设置成NULL zsl->tail = NULL; return zsl; }
在上述代码中调用了zslCreateNode这个函数,函数的源码如下所示=
zskiplistNode *zslCreateNode(int level, double score, robj *obj) { zskiplistNode *zn = zmalloc(sizeof(*zn)+level*sizeof(struct zskiplistLevel)); zn->score = score; zn->obj = obj; return zn; }
执行完上述代码之后会创建如下图所示的跳表结构
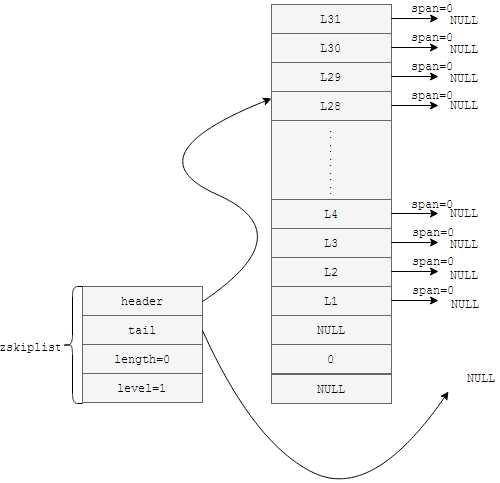
创建了跳表的基本结构,下面就是插入操作了,Redis中源码如下所示
zskiplistNode *zslInsert(zskiplist *zsl, double score, robj *obj) { zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x; //update[32] unsigned int rank[ZSKIPLIST_MAXLEVEL];//rank[32] int i, level; redisAssert(!isnan(score)); x = zsl->header; //寻找元素插入的位置 for (i = zsl->level-1; i >= 0; i--) { /* store rank that is crossed to reach the insert position */ rank[i] = i == (zsl->level-1) ? 0 : rank[i+1]; while (x->level[i].forward && (x->level[i].forward->score < score || //以下是得分相同的情况下,比较value的字典排序 (x->level[i].forward->score == score &&compareStringObjects(x->level[i].forward->obj,obj) < 0))) { rank[i] += x->level[i].span; x = x->level[i].forward; } update[i] = x; } //产生随机层数 level = zslRandomLevel(); if (level > zsl->level) { for (i = zsl->level; i < level; i++) { rank[i] = 0; update[i] = zsl->header; update[i]->level[i].span = zsl->length; } //记录最大层数 zsl->level = level; } //产生跳表节点 x = zslCreateNode(level,score,obj); for (i = 0; i < level; i++) { x->level[i].forward = update[i]->level[i].forward; update[i]->level[i].forward = x; //更新跨度 x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]); update[i]->level[i].span = (rank[0] - rank[i]) + 1; } //此种情况只会出现在随机出来的层数小于最大层数时 for (i = level; i < zsl->level; i++) { update[i]->level[i].span++; } x->backward = (update[0] == zsl->header) ? NULL : update[0]; if (x->level[0].forward) x->level[0].forward->backward = x; else zsl->tail = x; zsl->length++; return x; }
上述源码中,有一个产生随机层数的函数,源代码如下所示:
int zslRandomLevel(void) { int level = 1; //#define ZSKIPLIST_P 0.25 while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF)) level += 1; //#ZSKIPLIST_MAXLEVEL 32 return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL; }
图形化的形式描述如下图所示:
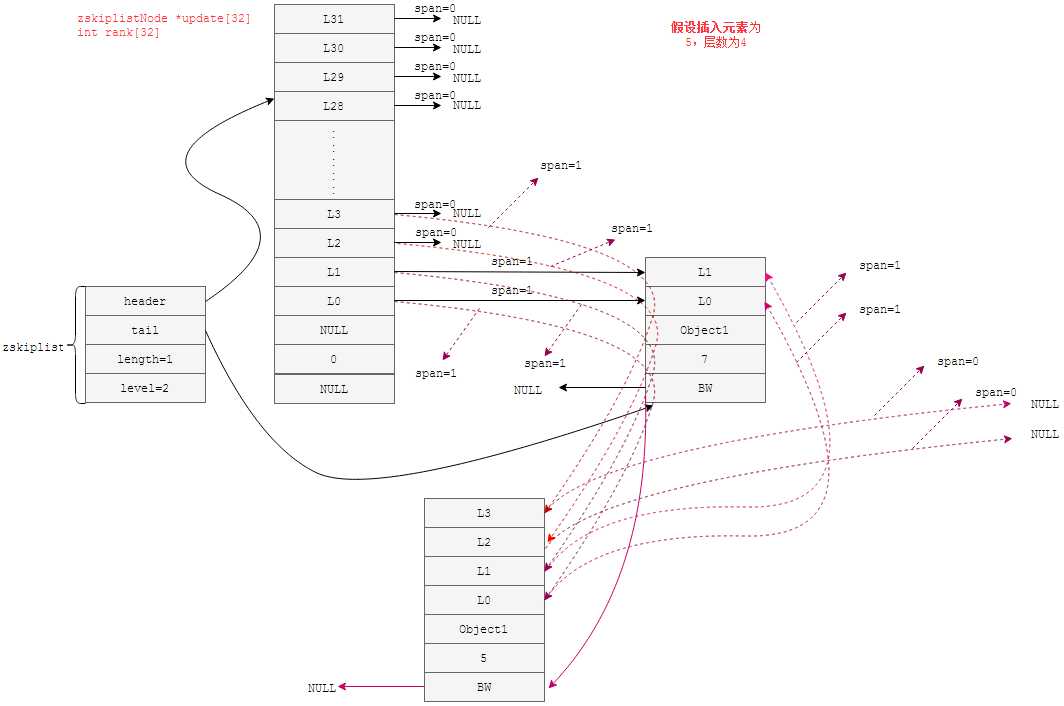
理解了插入操作,其他查询,删除,求范围操作基本上类似,此处忽略...
标签:
原文地址:http://www.cnblogs.com/WJ5888/p/4595306.html