标签:
K-MEANS算法: 输入:聚类个数k,以及包含 n个数据对象的数据。 输出:满足方差最小标准的k个聚类。
处理流程:
(1) 从 n个数据对象选择 k 个对象作为初始聚类中心;
(2) 循环(3)到(4)直到每个聚类不再发生变化为止
(3) 根据每个聚类对象的均值(中心对象),计算每个对象与这些中心对象的距离;并根据最小距离重新对相应对象进行划分;
(4) 重新计算每个(有变化)聚类的均值(中心对象)
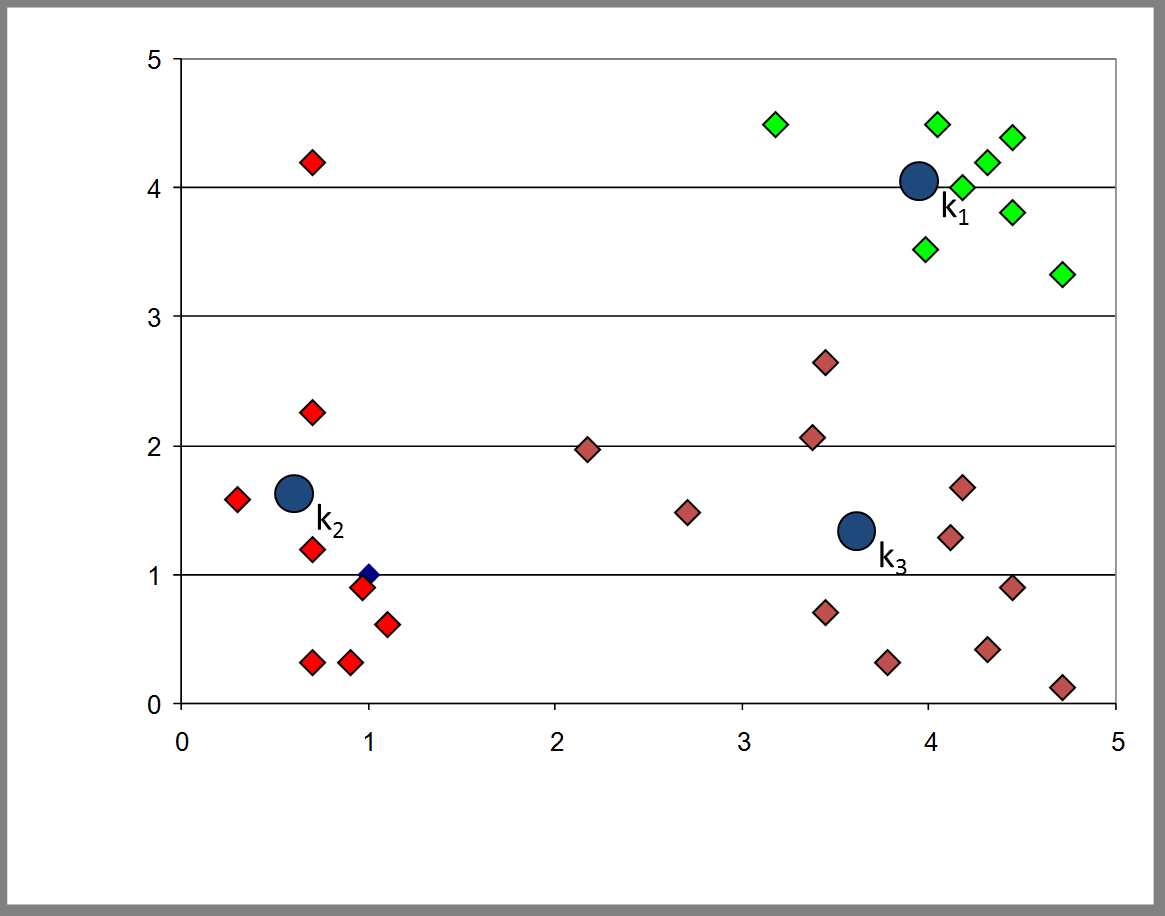
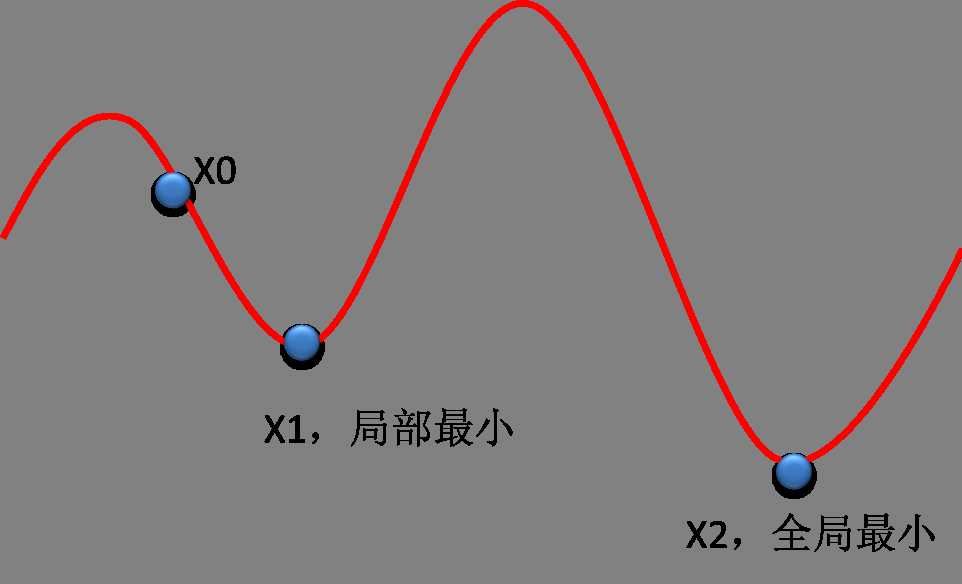
K means的结果与初始点的选择密切相关,往往陷于局部最优。
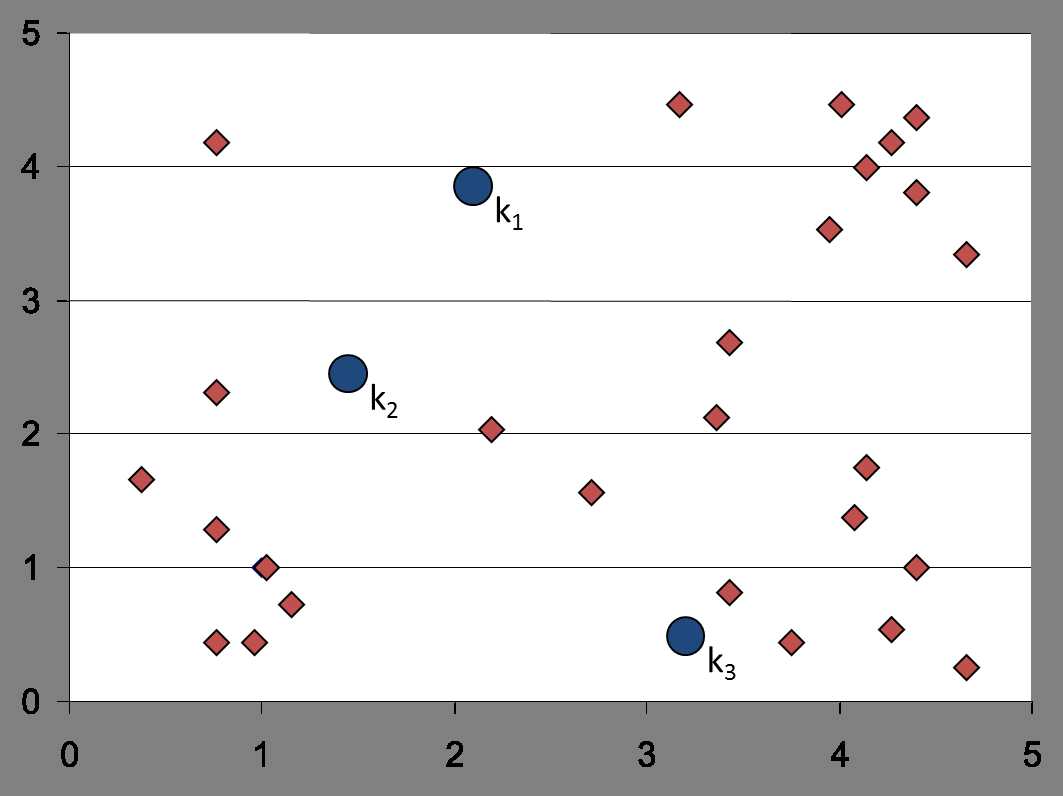
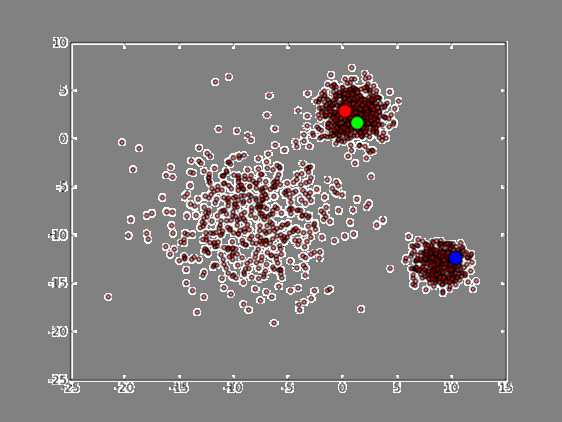
首先3个中心点被随机初始化,所有的数据点都还没有进行聚类,默认全部都标记为红色,如下图所示:
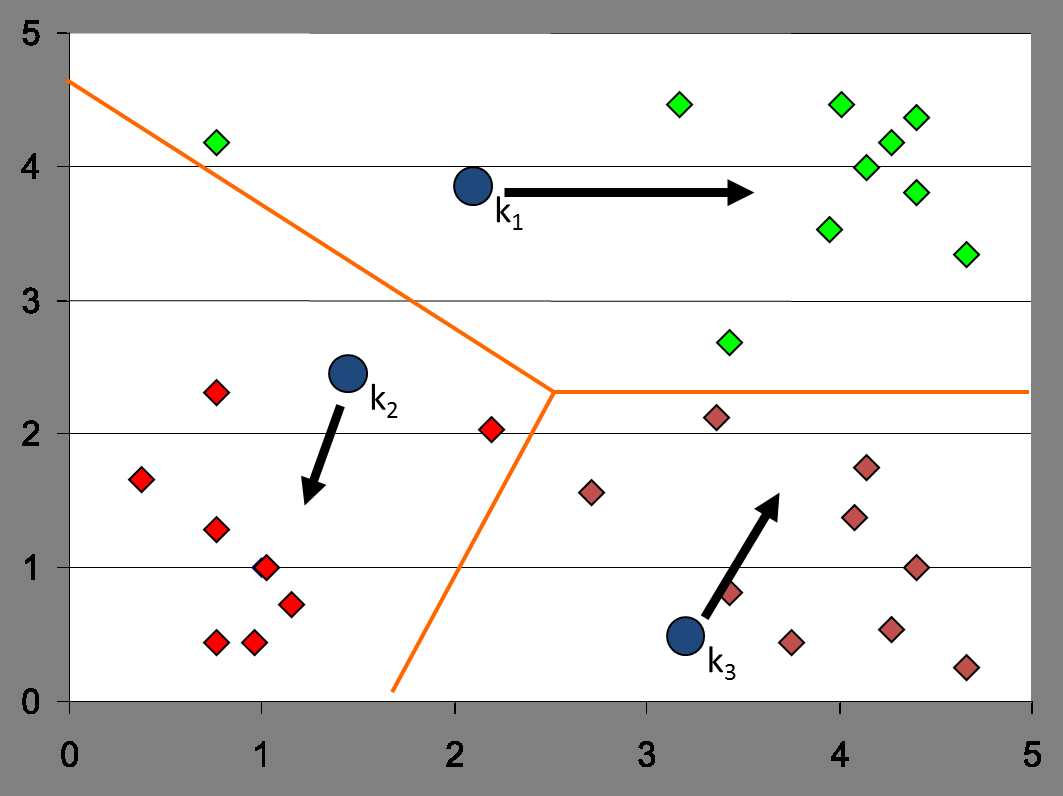
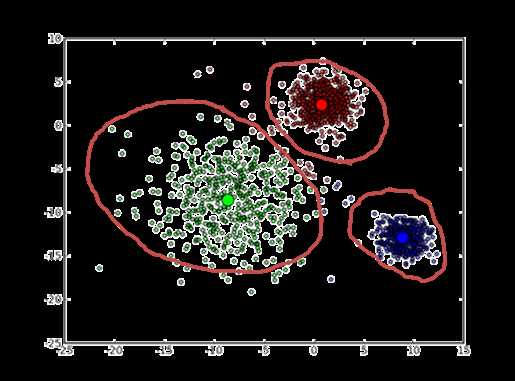
迭代最终结果如下:
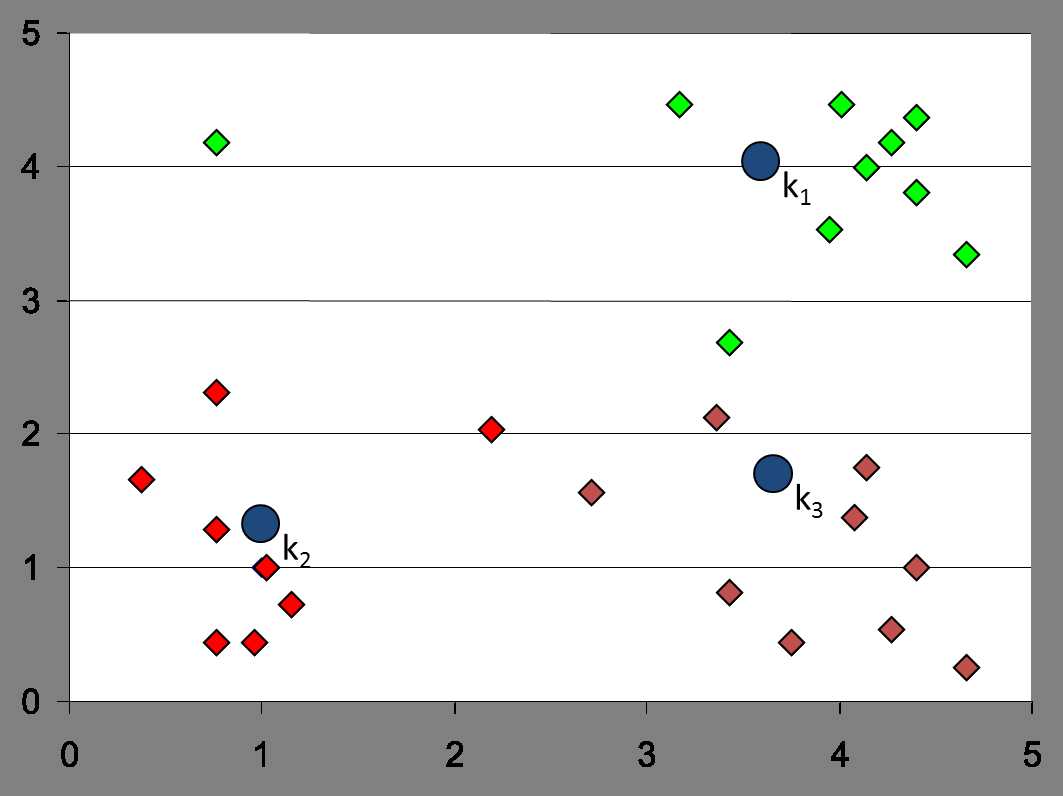
如果初始点为如下:
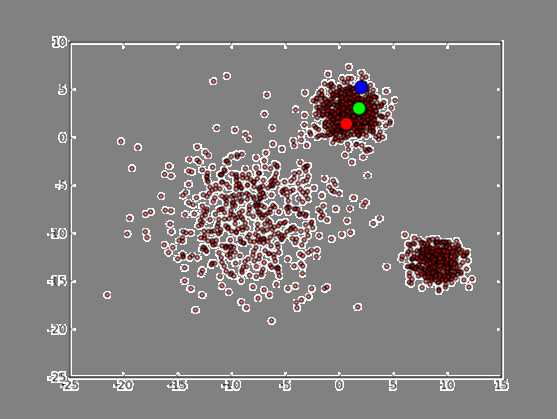
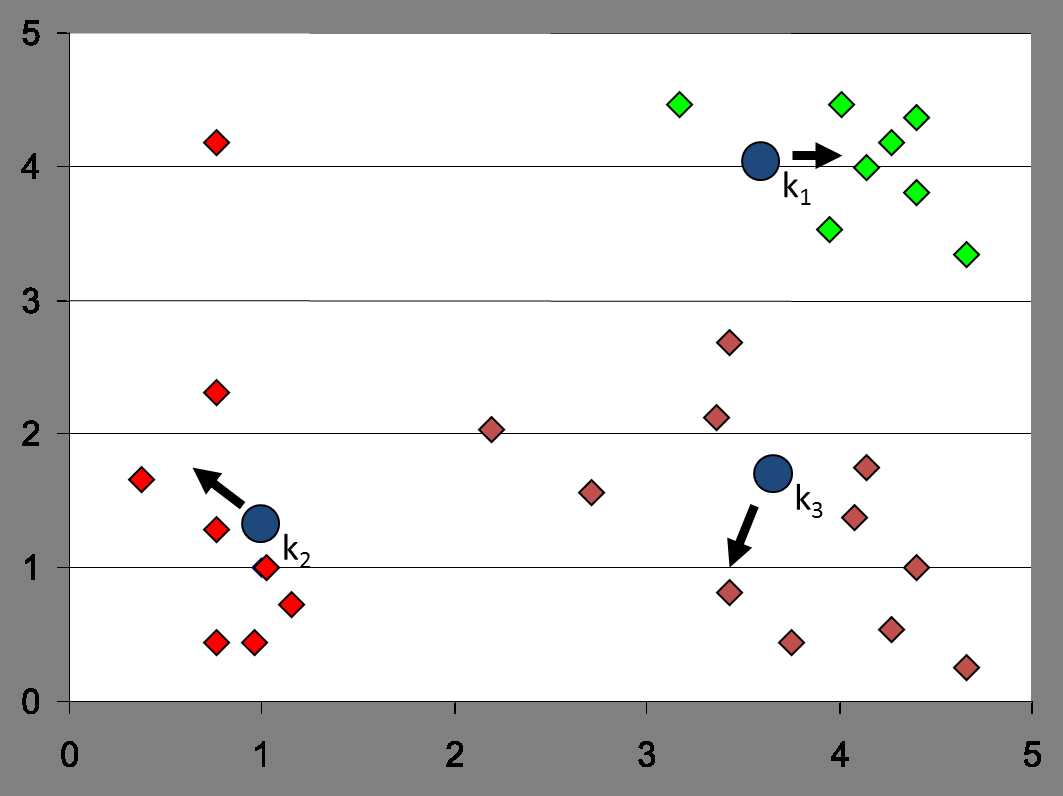
最终会收敛到这样的结果:
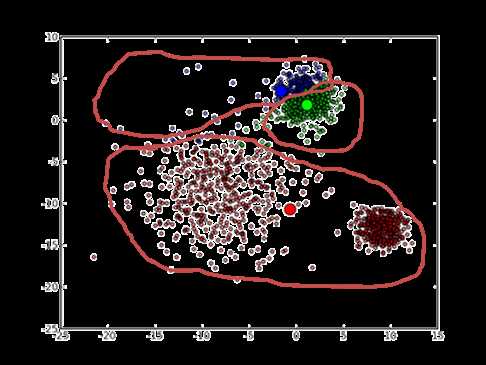
目前解决方法较多,但没有测底的解决方法。一般来说用户的初始种子点都是随机给的,或者是基于目视的,即进行多次聚类操作,选取相对最优的那个聚类,但这种方法不够自动。目前,研究较多的是将模拟退火、遗传算法等启发式算法与Kmeans聚类相结合,这样能大大降低陷于局部最优的困境。下图就是模拟退火的算法流程图。
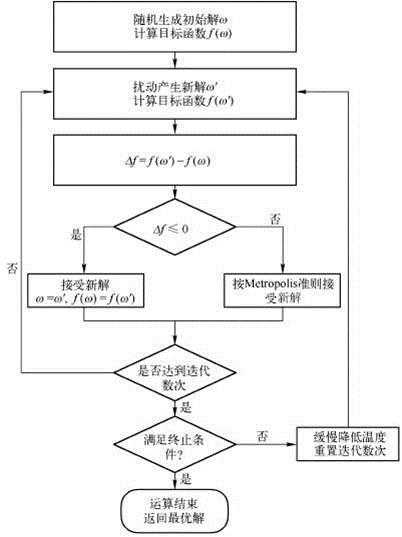
“纸上得来终觉浅,绝知此事要躬行”,仅知道原理而不去实践是永远不能深刻掌握某一知识的。本人用C++实现了基于模拟退火的Kmeans算法以及普通的Kmeans算法,来进行比较分析。
1)首先我们随机生成二维数据点以便用于聚类。
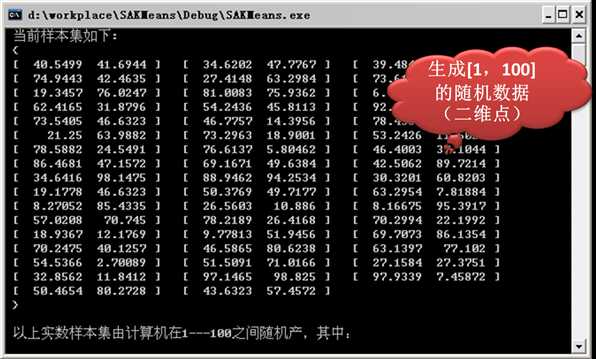
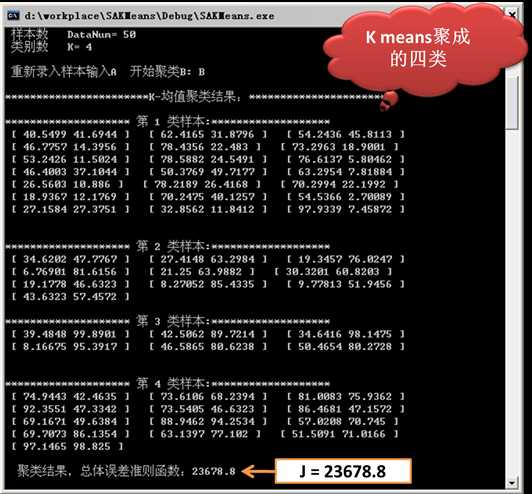
2)基于原生的Kmeans得到的结果。
3)基于模拟退火的Kmeans得到的结果
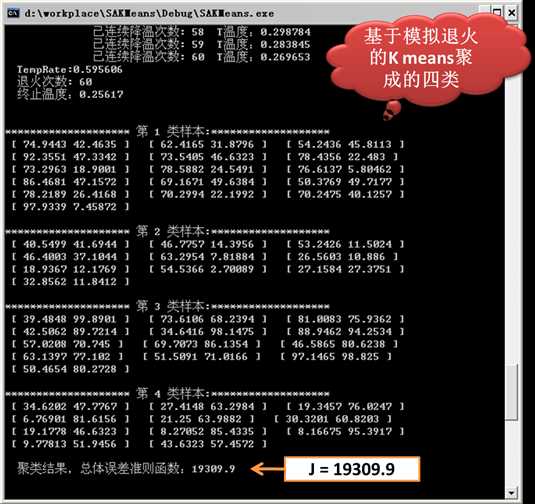
由上图的实验结果可以看出,基于模拟退火的K means所得的总体误差准则结果为:Jsa = 19309.9。
而普通的K means所得的总体误差准则结果为:Jnor = 23678.8。
可以看出基于模拟退火的K means所得的结果较好,当然,此算法的复杂度较高,收敛所需的时间较长。
标签:
原文地址:http://www.cnblogs.com/LBSer/p/4605440.html