标签:
题意:2-3树的每个结点(除了叶子外)有2或3个孩子(分支),假设是一个满2-3树,那么给出叶子的数量,求这样的树有多少棵。(注:有2个孩子的结点视为相同,有3个孩子的结点视为相同,比如倒数第2层有4个结点,且叶子有4+6=10个,即2个有2孩的结点在前面,2个有3孩的结点在后面,那么头两个结点的孩子互换是视为相同的,如下图)
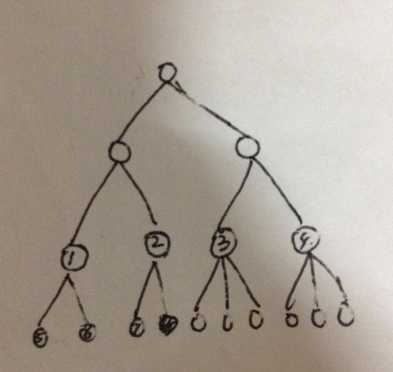
只要结点1234各自的孩子数不变,则视为同棵树。若具有2孩的结点跟具有3孩的结点换位置,则为不同树,比如1和3换个位置。)
思路:
(1)考虑DP,依靠叶子数量小的,推出叶子数量大的。dp[k]表示叶子数为k的树有多少棵。那么只有一个结点的情况dp[1]=1我们是知道的。
(2)如何dp?
dp[k]可以更新后面的点有dp[2k~3k],将k看成倒数第2层,那么其每个结点可以决定最底层的叶子个数。比如第1个结点生2孩,其他结点生3孩,可以更新dp[1*2+(k-1)*3]。
这一步只需要枚举2的个数即可,2的个数可以从0→k。设k=a+b,a个生2孩,b个生3孩,那么q=a*2+b*3为我们可以更新的点,则dp[q]+=dp[k]*c[k][a],这里c[k][a]的意思是组合数学中Ck取a的组合数。任何一个dp[x]都可能被多个不同的2-3树发展多一层而变来的,例如dp[3]可以更新dp[9],dp[4]当3个结点生2孩,1个结点生3孩也可以更新到dp[9],。
(3)需要预先求得c[x][y]的所有可能,因为后面可能多次引用,逐个计算复杂度会过高。

1 #include <bits/stdc++.h> 2 #define LL long long 3 using namespace std; 4 const int N=5005; 5 LL dp[N*3]; 6 LL c[N/2][N/2]; 7 8 unsigned int n,r; 9 void pre() //组合数,类似于一个黑色的袋子中摸出黑球和白球,黑白球代表2或3孩子,组成有序序列 10 { 11 memset(c,0,sizeof(c)); 12 c[0][0]=1; 13 c[1][0]=c[1][1]=1; 14 for(int i=2;i<=n/2;i++) 15 { 16 c[i][0]=1; 17 for(int j=1;j<i;j++) 18 c[i][j]=(c[i-1][j-1]%r+c[i-1][j]%r)%r; 19 20 c[i][i]=1; 21 } 22 } 23 void init() 24 { 25 memset(dp,0,sizeof(dp)); 26 dp[1]=1; 27 for(int i=1; i<n/2+1; i++) //从前面开始更新到后面,2500还能更新5000的,所以要循环到n/2 28 { 29 for(int j=0; j<=i; j++) //有j个2, i-j个3 30 { 31 int q=j*2+(i-j)*3; //要更新的点 32 dp[q]=(dp[q]+(dp[i]*c[i][j]))%r; 33 } 34 } 35 } 36 37 int main() 38 { 39 //freopen("e://input.txt", "r", stdin); 40 while(~scanf("%d%d",&n,&r)) 41 { 42 pre(); 43 init(); 44 printf("%lld\n",dp[n]); 45 } 46 return 0; 47 }
标签:
原文地址:http://www.cnblogs.com/xcw0754/p/4606011.html