标签:des style blog http color 使用
在上一篇文章《常用数据结构及复杂度》中,介绍了一些计算机程序设计中常用的线性数据结构,包括 Array、ArrayList、LinkedList<T>、List<T>、Stack<T>、Queue<T>、Hashtable 和 Dictionary<T> 等。并简单介绍了这些数据结构的内部实现原理和常用操作的运算复杂度,以及如何选择合适的数据结构。本篇文章中,我们将介绍常见的树形结构及其常用操作的运算复杂度。
我们知道像家谱族谱、公司组织结构等都是以树结构的形式组织数据。例如下图中所展示的公司组织结构图。
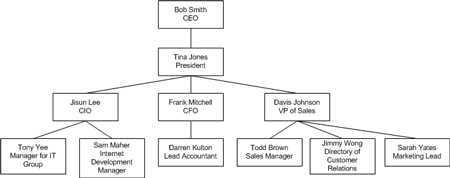
树(Tree)是由多个节点(Node)的集合组成,每个节点又有多个与其关联的子节点(Child Node)。子节点就是直接处于节点之下的节点,而父节点(Parent Node)则位于节点直接关联的上方。树的根(Root)指的是一个没有父节点的单独的节点。
所有的树都呈现了一些共有的特性:
二叉树(Binary Tree)是一种特殊的树类型,其每个节点最多只能有两个子节点。这两个子节点分别称为当前节点的左孩子(left child)和右孩子(right child)。
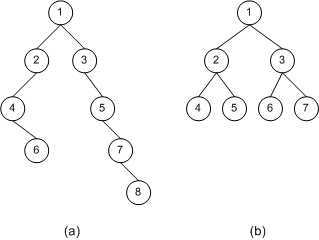
上图中,二叉树(a)包含 8 个节点,其中节点 1 是它的根节点。节点 1 的左孩子为节点 2,右孩子为节点 3。注意,并没有要求一个节点同时具有左孩子和右孩子。例如,二叉树(a)中,节点 4 就只有一个右孩子 6。此外,节点也可以没有孩子节点。例如,二叉树(b)中,节点 4、5、6、7 都没有孩子节点。
没有孩子的节点称为叶节点(Leaf Node),有孩子的节点则称为内节点(Internal Node)。如上图中,二叉树 (a) 中节点 6、8 为叶节点,节点 1、2、3、4、5、7 为内节点。
.NET 中并没有直接提供二叉树的实现,我们需要自己来实现 BinaryTree 类。在《你曾实现过二叉树吗》一文中,实现了一个基于泛型的简单的二叉树模型。
我们已经了解了数组是将元素连续地排列在内存当中,而二叉树却不是采用连续的内存存放。实际上,通常 BinaryTree 类的实例仅包含根节点(Root Node)实例的引用,而根节点实例又分别指向它的左右孩子节点实例,以此类推。所以关键的不同之处在于,组成二叉树的节点对象实例可以分散到 CLR 托管堆中的任何位置,它们没有必要像数组元素那样连续的存放。
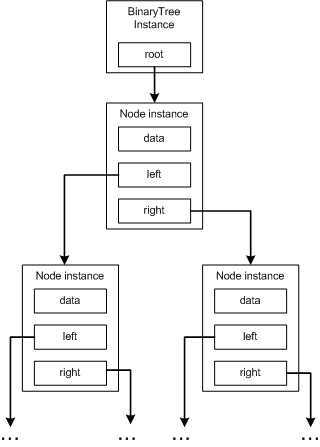
如果要访问二叉树中的某一个节点,通常需要逐个遍历二叉树中的节点,来定位那个节点。它不象数组那样能对指定的节点进行直接的访问。所以查找二叉树的渐进时间是线性的 O(n),在最坏的情况下需要查找树中所有的节点。也就是说,随着二叉树节点数量增加时,查找任一节点的步骤数量也将相应地增加。
那么,如果一个二叉树的查找时间是线性的,定位时间也是线性的,那相比数组来说到底哪里有优势呢?毕竟数组的查找时间虽然是线性 O(n),但定位时间却是常量 O(1) 啊?的确是这样,通常来说普通的二叉树确实不能提供比数组更好的性能。然而,如果我们按照一定的规则来组织排列二叉树中的元素时,就可以很大程度地改善查询时间和定位时间。
二叉查找树(BST:Binary Search Tree)是一种特殊的二叉树,它改善了二叉树节点查找的效率。二叉查找树有以下特性:
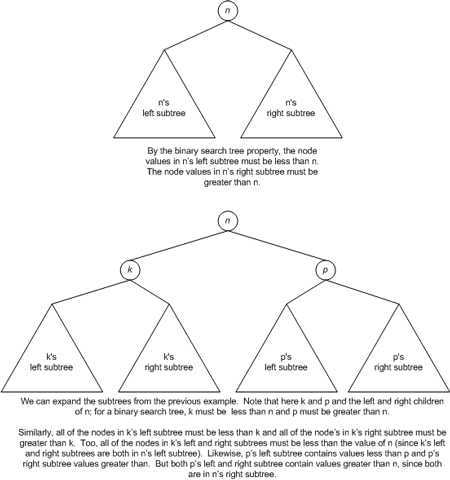
对于任意一个节点 n,
所谓节点 n 的子树,可以将其看作是以节点 n 为根节点的树。子树的所有节点都是节点 n 的后代,而子树的根则是节点 n 本身。
下图中展示了两个二叉树。二叉树(b)是一个二叉查找树(BST),它符合二叉查找树的特性规定。而二叉树(a),则不是二叉查找树。因为节点 10 的右孩子节点 8 小于节点 10,但却出现在节点 10 的右子树中。同样,节点 8 的右孩子节点 4 小于节点 8,但出现在了它的右子树中。无论是在哪个位置,只要不符合二叉查找树的特性规定,就不是二叉查找树。例如,节点 9 的左子树只能包含值小于节点 9 的节点,也就是 8 和 4。
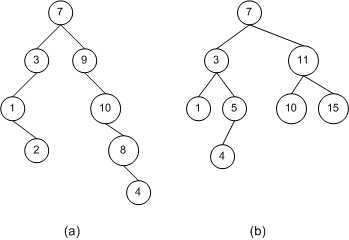
从二叉查找树的特性可知,BST 各节点存储的数据必须能够与其他的节点进行比较。给定任意两个节点,BST 必须能够判断这两个节点的值是小于、大于还是等于。
假设我们要查找 BST 中的某一个节点。例如在上图中的二叉查找树(b)中,我们要查找值为 10 的节点。
我们从根开始查找。可以看到,根节点的值为 7,小于我们要查找的节点值 10。因此,如果节点 10 存在,必然存在于其右子树中,所以应该跳到节点 11 继续查找。此时,节点值 10 小于节点 11 的值,则节点 10 必然存在于节点 11 的左子树中。在查找节点 11 的左孩子,此时我们已经找到了目标节点 10,定位于此。
如果我们要查找的节点在树中不存在呢?例如,我们要查找节点 9。重复上述操作,直到到达节点 10,它大于节点 9,那么如果节点 9 存在,必然存在于节点 10 的左子树中。然而我们看到节点 10 根本就没有左孩子,因此节点 9 在树中不存在。
总结来说,我们使用的查找算法过程如下:
假设我们要查找节点 n,从 BST 的根节点开始。算法不断地比较节点值的大小直到找到该节点,或者判定不存在。每一步我们都要处理两个节点:树中的一个节点,称为节点 c,和要查找的节点 n,然后并比较 c 和 n 的值。开始时,节点 c 为 BST 的根节点。然后执行以下步骤:
通过 BST 查找节点,理想情况下我们需要检查的节点数可以减半。如下图中的 BST 树,包含了 15 个节点。从根节点开始执行查找算法,第一次比较决定我们是移向左子树还是右子树。对于任意一种情况,一旦执行这一步,我们需要访问的节点数就减少了一半,从 15 降到了 7。同样,下一步访问的节点也减少了一半,从 7 降到了 3,以此类推。
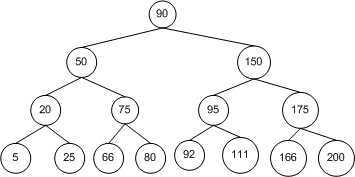
根据这一特点,查找算法的时间复杂度应该是 O(log2n),简写为 O(lg n)。我们在文章《算法复杂度分析》中有一些关于时间复杂度的描述。可知,log2n = y,相当于 2y = n。即,如果节点数量增加 n,查找时间只缓慢地增加到 log2n。下图中显示了 O(log2n) 和线性增长 O(n) 的增长率之间的区别。时间复杂度为 O(log2n) 的算法运行时间为下面那条线。
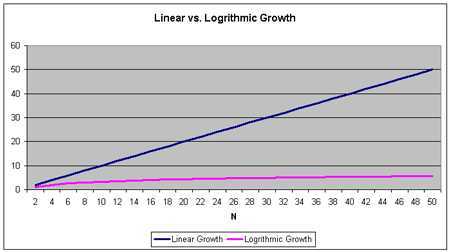
从上图可以看出,O(log2n) 曲线几乎是水平的,随着 n 值的增加,曲线增长十分缓慢。举例来说,查找一个具有 1000 个元素的数组,需要查询 1000 个元素,而查找一个具有 1000 个元素的 BST 树,仅需查询不到10 个节点(log21024 = 10)。
而实际上,对于 BST 查找算法来说,其十分依赖于树中节点的拓扑结构,也就是节点间的布局关系。下图描绘了一个节点插入顺序为 20, 50, 90, 150, 175, 200 的 BST 树。这些节点是按照递升顺序被插入的,结果就是这棵树没有广度(Breadth)可言。也就是说,它的拓扑结构其实就是将节点排布在一条线上,而不是以扇形结构散开,所以查找时间也为 O(n)。
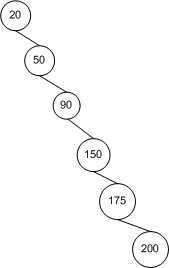
当 BST 树中的节点以扇形结构散开时,对它的插入、删除和查找操作最优的情况下可以达到亚线性的运行时间 O(log2n)。因为当在 BST 中查找一个节点时,每一步比较操作后都会将节点的数量减少一半。尽管如此,如果拓扑结构像上图中的样子时,运行时间就会退减到线性时间 O(n)。因为每一步比较操作后还是需要逐个比较其余的节点。也就是说,在这种情况下,在 BST 中查找节点与在数组(Array)中查找就基本类似了。
因此,BST 算法查找时间依赖于树的拓扑结构。最佳情况是 O(log2n),而最坏情况是 O(n)。
我们不仅需要了解如何在二叉查找树中查找一个节点,还需要知道如何在二叉查找树中插入和删除一个节点。
当向树中插入一个新的节点时,该节点将总是作为叶子节点。所以,最困难的地方就是如何找到该节点的父节点。类似于查找算法中的描述,我们将这个新的节点称为节点 n,而遍历的当前节点称为节点 c。开始时,节点 c 为 BST 的根节点。则定位节点 n 父节点的步骤如下:
当合适的节点找到时,该算法结束。从而使新节点被放入 BST 中成为某一父节点合适的孩子节点。
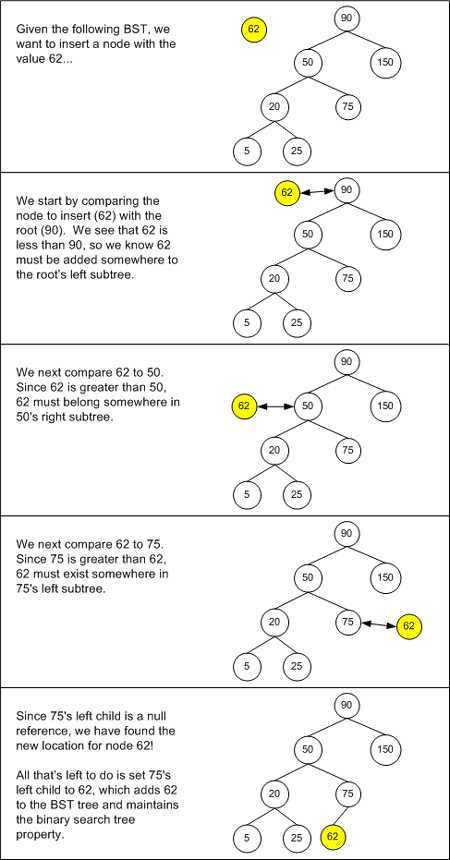
BST 的插入算法的复杂度与查找算法的复杂度是一样的:最佳情况是 O(log2n),而最坏情况是 O(n)。因为它们对节点的查找定位策略是相同的。
从 BST 中删除节点比插入节点难度更大。因为删除一个非叶子节点,就必须选择其他节点来填补因删除节点所造成的树的断裂。如果不选择节点来填补这个断裂,那么就违背了 BST 的特性要求。
删除节点算法的第一步是定位要被删除的节点,这可以使用前面介绍的查找算法,因此运行时间为 O(log2n)。接着应该选择合适的节点来代替删除节点的位置,它共有三种情况需要考虑。
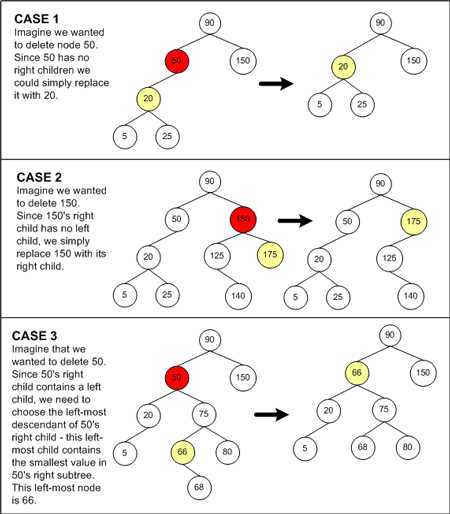
我们知道,在 BST 中,最小值的节点总是在最左边,最大值的节点总是在最右边。因此替换被删除节点右子树中最小的一个节点,就保证了该节点一定大于被删除节点左子树的所有节点。同时,也保证它替代了被删除节点的位置后,它的右子树的所有节点值都大于它。因此这种选择策略符合二叉查找树的特性。
和查找、插入算法类似,删除算法的运行时间也与 BST 的拓扑结构有关,最佳情况是 O(log2n),而最坏情况是 O(n)。
对于线性的连续的数组来说,遍历数组采用的是单向的迭代法。从第一个元素开始,依次向后迭代每个元素。而 BST 则有三种常用的遍历方式:
当然,这三种遍历方式的工作原理是类似的。它们都是从根节点开始,然后访问其子节点。区别在于遍历时,访问节点本身和其子节点的顺序不同。
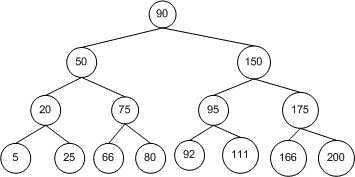
前序遍历(Perorder traversal)
前序遍历从当前节点(节点 c)开始访问,然后访问其左孩子,再访问右孩子。开始时,节点 c 为 BST 的根节点。算法如下:
则上图中树的遍历结果为:90, 50, 20, 5, 25, 75, 66, 80, 150, 95, 92, 111, 175, 166, 200。
中序遍历(Inorder traversal)
中序遍历是从当前节点(节点 c)的左孩子开始访问,再访问当前节点,最后是其右节点。开始时,节点 c 为 BST 的根节点。算法如下:
则上图中树的遍历结果为:5, 20, 25, 50, 66, 75, 80, 90, 92, 95, 111, 150, 166, 175, 200。
后序遍历(Postorder traversal)
后序遍历首先从当前节点(节点 c)的左孩子开始访问,然后是右孩子,最后才是当前节点本身。开始时,节点 c 为 BST 的根节点。算法如下:
则上图中树的遍历结果为:5, 25, 20, 66, 80, 75, 50, 92, 111, 95, 166, 200, 175, 150, 90。
实际上,BST 操作的运行时间与树的高度(Height)是有关系的。一个树的高度指的是从树的根开始所能到达的最长的路径长度。树的高度可被递归性地定义为:
计算树的高度要从叶子节点开始,首先将叶子节点的高度置为 0,然后根据上面的规则向上计算父节点的高度。以此类推直到树中所有的节点高度都被标注后,则根节点的高度就是树的高度。
下图显示了几棵已经计算好高度的 BST 树。
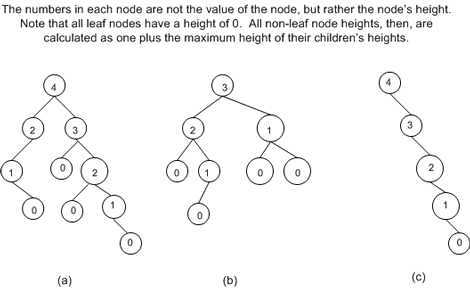
如果树中节点的数量为 n,则一棵满足O(log2n) 渐进运行时间的 BST 树的高度应接近于比 log2n 小的最大整数。
上图中的三棵 BST 树中,树(b)拥有最好的高度与节点数量的比例。树(b)的高度为 3 ,节点数量为 8,所以 log28 = 3,结果正好与树的高度相等。
树(a)的节点数量为 10,而高度为 4,log210 = 3.3219,比 3.3219 小的最大整数是 3,所以树(a)最理想的高度应该为 3。我们可以通过移动距离最远的节点到中间的某个非叶子节点,以减少数的高度,以使该树的高度与节点数量的比例达到最优。
树(c)的情况是最差的,它的节点数量是 5,所以log25 = 2.3219,则理想高度为 2,但实际上是 4。
实际上我们真正面对的问题是如何保证 BST 的拓扑结构始终保持树高度与节点数量的最佳比例。因为 BST 的拓扑结构与节点的插入顺序息息相关,一种方式是通过数据的乱序来保证。如果在向树中插入节点前就可以得到数据还好说,而如果我们无法掌控数据的来源呢?比如,数据来自用户的输入,或者来自传感器的实时数据等,基本上要保证数据乱序是没希望了。那么,另一种方案就是在不试图让数据源决定数据顺序的情况下,新的节点插入后仍然可以保持 BST 树的平衡(balanced)。这种能够始终维持树平衡状态的数据结构称为自平衡二叉查找树(self-balancing binary search tree)。
一棵平衡树指的是树能够保持其高度与广度能够保持预先定义的比例。不同的数据结构可以定义不同的比例以保持平衡,但所有的比例都趋向于log2n。那么,一颗自平衡的 BST 也同样呈现出 O(log2n) 的渐进运行时间。
有许多种不同的自平衡 BST 数据结构,例如 AVL 树、红黑树(Red-Black Tree)、2-3 树、2-3-4 树、伸展树(Splay Tree)、B 树等等。本文中我们将简要介绍其中的两种:AVL 树和红黑树。
在 1962 年,俄罗斯数学家 G. M. Andel‘son-Vel-skii 和 E. M. Landis 发明了第一种自平衡二叉查找树,叫做 AVL 树。AVL 树必须维持如下平衡条件,对每个节点 n:
节点的左子树或者右子树的高度可以通过上面描述的步骤来计算。如果节点仅有一个子节点,则无子节点侧的高度为 -1。
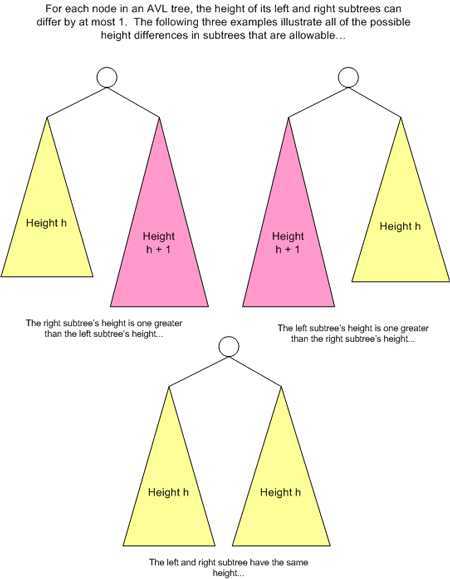
下图展示了概念上 AVL 树节点的两侧子树高度需要保持的关系。
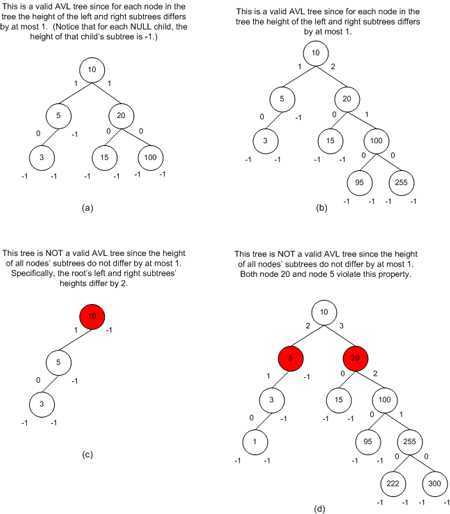
下面是一些 BST 树。节点中的数字代表着节点的值,左右两侧的数字代表着左右子树的高度。其中树(a)和树(b)是合法的 AVL 树,而树(c)和树(d)则不合法,因为树中不是所有的节点都满足 AVL 的平衡特性要求。
当创建一棵 AVL 树时,难点在于如何保证 AVL 的平衡特性要求,而不用关注对树的具体操作。也就是说,无论是向树添加节点还是删除节点,最重要的事情就是保持树的平衡。AVL 树通过 "旋转操作(rotations)" 来保持树的平衡。旋转操作可以重塑树的拓扑结构来恢复树的平衡,更重要的是,重塑后的树依然符合二叉查找树的特性要求。
当向一棵 AVL 树中插入一个新的节点时,需要经过两阶段的过程。首先,插入新节点的操作将使用与向 BST 树中插入新节点时使用的相同的查找算法。新的节点将做为一个叶子节点被添加到树中合适的位置,以满足 BST 的特性要求。在添加完节点后,将导致树的结构可能已经违背 AVL 树的特性要求。所以在第二个阶段中,将遍历访问路径,来检查每个节点左右子树高度。如果存在某节点的左右子树的高度差大于 1 时,则需要使用旋转操作来处理。
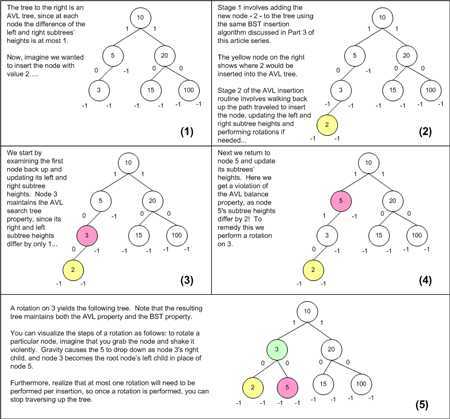
下图阐述了对节点 3 进行旋转操作的步骤。在阶段一插入新节点 2 后,在节点 5 处的 AVL 树的平衡特性已经被破坏,因为节点 5 的左右子树的差为 2,大于 AVL 树要求的 1。为了解决这个问题,需要在节点 5 的左子树的根节点,也就是节点 3 处做旋转操作。这个旋转操作不仅恢复了 AVL 树的平衡要求,而且也保持了 BST 的特性要求。
有时除了像上图中描述的简单的旋转操作之外,可能还需要进行多次旋转操作。对于成组的旋转操作的深入讨论已经超出了本篇文章的范畴,这里就不再赘述了。最重要的就是要意识到插入操作和删除操作都会破坏 AVL 树的平衡,而旋转操作就是解决这些问题的法宝。
通过确保所有节点的左右子树的差小于等于 1,AVL 树保证了插入、删除和查找操作将始终保持 O(log2n) 的渐进运行时间,而与插入或删除节点的顺序无关。
在 1972 年,慕尼黑理工大学(Technical University of Munich)的计算机科学家 Rudolf Bayer 创造了红黑树(Red-Black Tree)数据结构。除了包含数据和左右孩子节点之外,红黑树的节点还包含了一项特别的信息 -- 颜色。这个颜色只包含两种颜色,即红色和黑色。并且,红黑树还添加了一种特殊类型的节点,称为 NIL 节点。NIL 节点将做为红黑树的伪叶子节点出现。也就是说,所有带有关键数据的节点称为内节点,而所有其他的外节点则均指向 NIL 节点。这个概念可能理解起来有些费劲,希望下面这张图有所帮助。
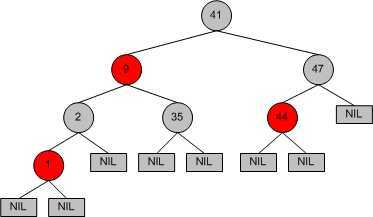
红黑树(R-B Tree)需要满足如下特性:
前面几条特性都很好解释,只有最后一条最难理解。简单的说,从树中任意一个节点开始,从该节点到其后代的任意一个 NIL 节点的路径上的黑色节点的数量必须相同。比如上图中,以根节点为例,从节点 41 到任意一个 NIL 节点的路径上,黑色节点的数量都是相同的,也就是 3 个。如从节点 41 到左下角的 NIL 节点的路径上,黑色节点包括 41, 2, NIL,所以黑色节点数量是 3 个。
类似于 AVL 树,红黑树也是一种自平衡二叉查找树。AVL 树的平衡特性是通过限制节点的左右子树的高度来达成,而红黑树则是通过更形象化的方式来保证树的平衡。如果一棵树满足红黑树的特性,其节点的总数量为 n,则它的高度将始终小于 2 * log2(n+1) 。鉴于这个原因,致使红黑树保证了对树的所有操作都能在 O(log2n) 渐进运行时间范围内。
同样是和 AVL 树一样,当对红黑树进行节点的插入和删除时,最终要的就是使其仍然符合红黑树的特性。AVL 树通过使用旋转操作(rotations)来恢复树的平衡。而红黑树则是通过重新着色(recoloring)和旋转两种操作共同来完成。这不仅需要判断节点的父节点的颜色,还需要对比叔父节点的颜色,使得红黑树的恢复过程变得更加复杂。
向红黑树中插入新的节点时,需要考虑很多种情况。假设已存在红黑树 T,即将被插入的新节点为 K。
首先一种特殊情况就是如果树 T 为空,则可直接将节点 K 设置为根节点,并且将颜色标为黑色,这样即可满足 R-B 树的所有要求。
如果树 T 不为空,则需要遵循如下步骤:
我们知道 BST 树总是将新节点添加为叶子节点,所以将节点 K 插入到树 T 中不会破坏根特性。而添加一个红色的叶子节点也不会影响树 T 的黑特性。实际上,添加一个红色的叶子节点仅有可能影响树 T 的红特性,所以我们仅需检查树的红特性,如果红特性被违背,则需要重塑树结构以重新满足红黑树特性。
我们将节点 K 的父节点称为节点 P(parent node),将节点 P 的父节点称为节点 G(grandparent node),将节点 P 的兄弟节点称为节点 S(sibling node)。
当向非空树 T 中插入节点 K 时,将直接受到父节点 P 的颜色的影响,可能会遇到如下多种情况。
情况1:节点 P 是黑色。
如果 P 为黑色,而节点 K 为红色,所以实际上不会违背红特性,则树 T 已经满足所有红黑树特性条件。
情况2:节点 P 是红色。
如果节点 P 为红色,那么 P 现在有了新的子节点 K,并且 K 也为红色,所以已经违背了红特性。为了处理这种两个红节点的情况,我们需要考虑节点 G 的其他子节点,也就是节点 P 的兄弟节点 S。此时,会有两种情况发生:
情况 2a:节点 S 是黑色或者为空。
如果节点 S 是黑色或者为空,则需要对节点 K、P、G 进行旋转。根据 K、P、G 顺序的不同,旋转操作可能存在四种可能性。
前两种可能性为当 P 为 G 的左子节点时。
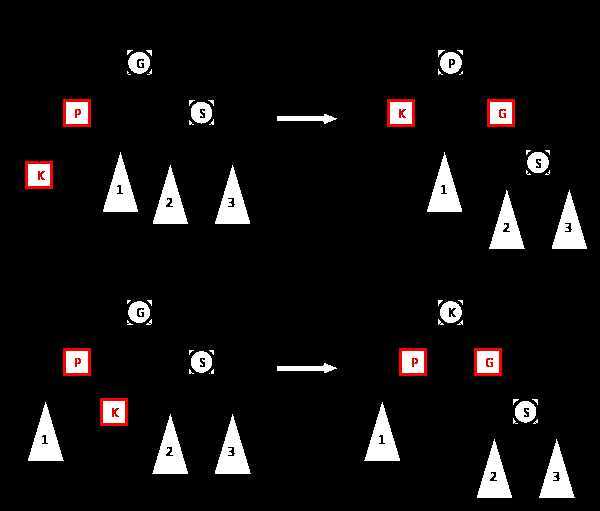
如果 S 为空,则上图中直接将 S 删除即可。
另两种可能性为当 P 为 G 的右子节点时,正好与上面图中的过程相反。
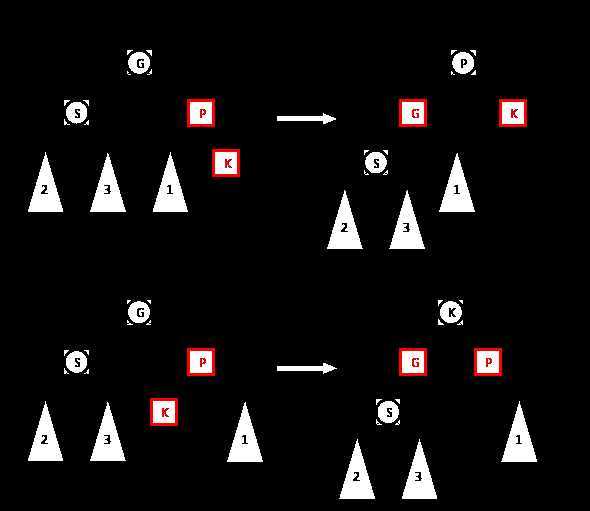
旋转操作过程结束后,双红节点情况已经被合理的解决了。
情况 2b:节点 S 是红色。
如果 P 的兄弟节点 S 是红色,则需要对 P、S、G 进行重新着色:将 P 和 S 着色为黑色,将 G 着色为红色。
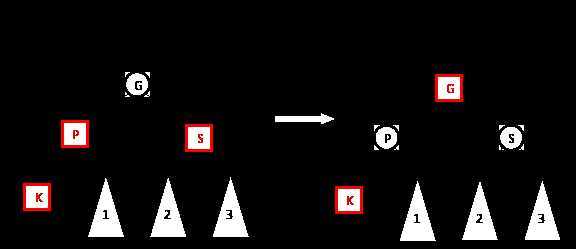
重新着色操作不会影响树 T 的黑特性,因为当 P、G 的颜色更改时,所有路径上的黑色节点数量并没有改变。但是,重新着色可能会使 G 和 G 的父节点产生双红情况。这种情况下,则需要从 G 和 G 的父节点开始继续遵循处理 K 和 K 的父节点的方式递归式地解决双红问题。
对于红黑树深入的讨论不在本文的范畴,这里不再赘述。
参考资料
本文《二叉树结构及复杂度》由 Dennis Gao 发表自博客园博客,任何未经作者本人允许的人为或爬虫转载均为耍流氓。
标签:des style blog http color 使用
原文地址:http://www.cnblogs.com/gaochundong/p/understanding_binary_trees.html