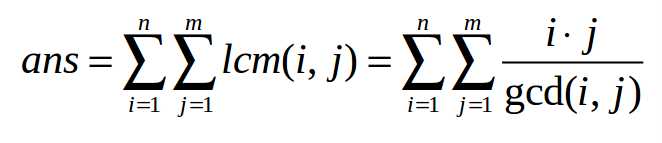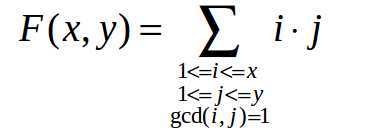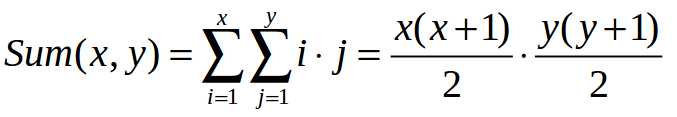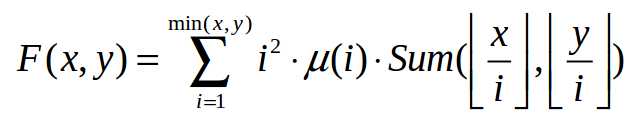BZOJ 2154: Crash的数字表格

Description

今天的数学课上，Crash小朋友学习了最小公倍数(Least Common Multiple)。对于两个正整数a和b，LCM(a, b)表示能同时被a和b整除的最小正整数。例如，LCM(6, 8) = 24。回到家后，Crash还在想着课上学的东西，为了研究最小公倍数，他画了一张N*M的表格。每个格子里写了一个数字，其中第i行第j列的那个格子里写着数为LCM(i, j)。一个4*5的表格如下： 1 2 3 4 5 2 2 6 4 10 3 6 3 12 15 4 4 12 4 20 看着这个表格，Crash想到了很多可以思考的问题。不过他最想解决的问题却是一个十分简单的问题：这个表格中所有数的和是多少。当N和M很大时，Crash就束手无策了，因此他找到了聪明的你用程序帮他解决这个问题。由于最终结果可能会很大，Crash只想知道表格里所有数的和mod 20101009的值。

HINT

N, M ≤ 107。

Solution

依旧暴力写开

依旧枚举d=gcd

再令

于是得到

愉快地推完了//跪PoPoQQQ神推

  1 #include<map>
  2 #include<cmath>
  3 #include<ctime>
  4 #include<queue>
  5 #include<stack>
  6 #include<cstdio>
  7 #include<climits>
  8 #include<iomanip>
  9 #include<cstring>
 10 #include<cstdlib>
 11 #include<iostream>
 12 #include<algorithm>
 13 
 14 #define mod 100000009
 15 #define maxn 10000000+5
 16 #define set(a,b) memset(a,(b),sizeof(a))
 17 #define fr(i,a,b) for(ll i=(a),_end_=(b);i<=_end_;i++)
 18 #define rf(i,b,a) for(ll i=(a),_end_=(b);i>=_end_;i--)
 19 #define fe(i,a,b) for(int i=first[(b)],_end_=(a);i!=_end_;i=s[i].next)
 20 #define fec(i,a,b) for(int &i=cur[(b)],_end_=(a);i!=_end_;i=s[i].next)
 21 
 22 using namespace std;
 23 
 24 typedef long long ll;
 25 
 26 ll f[maxn];
 27 int prime[maxn],pri[maxn],miu[maxn],tot=0;
 28 ll ans;
 29 int n,m;
 30 
 31 void read()
 32 {
 33 #ifndef ONLINE_JUDGE
 34   freopen("2154.in","r",stdin);
 35   freopen("2154.out","w",stdout);
 36 #endif
 37   cin >> n >> m ;
 38 }
 39 
 40 void write()
 41 {
 42   cout << (ans+mod)%mod ;
 43 }
 44 
 45 void get()
 46 {
 47   miu[1]=1;
 48   fr(i,2,min(n,m)){
 49     if( !prime[i] ) pri[++tot]=i,miu[i]=-1;
 50     int j=1;
 51     while( j<=tot && pri[j]*i<=min(n,m) ){
 52       prime[ pri[j]*i ]=1;
 53       if( i%pri[j]==0 ){
 54     miu[pri[j]*i]=0;
 55     break;
 56       }
 57       miu[pri[j]*i]=-miu[i];
 58       j++;
 59     }
 60   }
 61   fr(i,1,min(n,m))
 62     f[i]=(f[i-1]+i*i*miu[i]%mod)%mod;
 63 }
 64 
 65 ll Sum(ll x,ll y)
 66 {
 67   return ((x+1)*x/2%mod)*((y+1)*y/2%mod)%mod;
 68 }
 69 
 70 ll F(ll x,ll y)
 71 {
 72   ll res=0,i=1,pos;
 73   while( i<=x ){
 74     pos=min(x/(x/i),y/(y/i));
 75     res=(res+(f[pos]-f[i-1])*Sum(x/i,y/i)%mod)%mod;
 76     i=pos+1;
 77   }
 78   return res;
 79 }
 80 
 81 ll calc(ll x,ll y)
 82 {
 83   if( x>y ) swap(x,y);
 84   ll res=0,i=1,pos;
 85   while( i<=x ){
 86     pos=min(x/(x/i),y/(y/i));
 87     res=(res+(pos-i+1)*(pos+i)/2%mod*F(x/i,y/i)%mod)%mod;
 88     i=pos+1;
 89   }
 90   return res;
 91 }
 92 
 93 void work()
 94 {
 95   get();
 96   ans=calc(n,m);
 97 }
 98 
 99 int main()
100 {
101   read();
102   work();
103   write();
104   return 0;
105 }

标签：

原文地址：http://www.cnblogs.com/ST-Saint/p/4614865.html