标签：
SVM是用来解决非线性分类问题的。
首先我们假设样本线性可分【稍后我们还会去掉这个假设】
我们把之前logistic回归里面吗定义的那一坨稍微修改一下：
令
g(z)=1 (z>=0) or -1 (z<0) ，即y[i]∈{1,-1}
$h_{w,b}\left( x\right) =g\left( w^{T}x+b\right)$
(注：在原来定义的 $\theta ^ {T}x $中，θ是n+1维的(θ[0]....θ[n]) ，然而这里w是n维向量，b是常数，w就相当于原来的θ[1]....θ[n]，b相当于θ[0])
定义两个重要的概念：
1.1函数间隔（Functional Margin）
对于某个训练样本(x[i],y[i]) ，定义函数间隔为
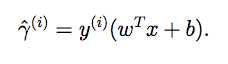
整个集合的函数间隔为其中最小的一个
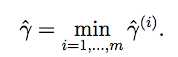
函数间隔的意义：
再回忆一下之前学习logistic回归时g函数的那个S形的图像，当wx+b的绝对值很大时，g→1，这时我们可以认为它有很大可能性属于被归为的这一类。那么这时若y[i]与其符号相同，说明归类正确，因而函数间隔为正。否则说明归类错误，函数间隔为负。
因此，整个集合的函数间隔的大小可以用来衡量归类的准确度
注1.1.1：对于等式k·wx+k·b=0，任意改变k的值并不会影响原有的超平面（只要不是0）。
1.2几何间隔（Geometric Margin）
上一张图：
样本i的几何间隔为：
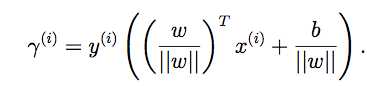
对于整个训练集合，几何间隔为：
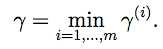
另外由上面两个定义可以得出，函数间隔=几何间隔*||w|| 【||w||是w的绝对值
核心思想：选择合适的w和b，使得几何间隔最大
形式化的写法如下：
1. 【约定||w||=1 （根据上面的注1.1.1，||w||的值可以任意放缩）
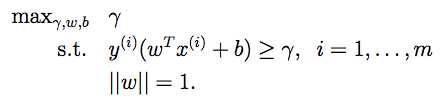
2.
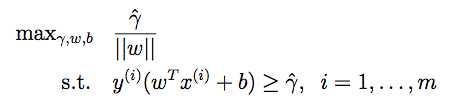
3.
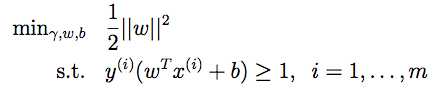
这些式子的结果就是最优间隔分类。可以用二次规划的方法去求解。
Lagrange乘数法用来求在约束条件下的函数最值。大一高数课曾经学过这东西-.-
举几个栗子：
Q3.1
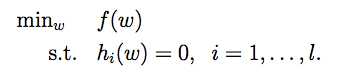
A3.1
STEP1：作lagrange函数
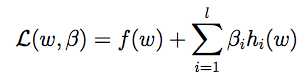（β是求解用的参数）
STEP2：将L对每个参数求偏导，令偏导数值等于0
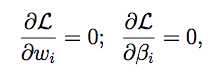
然后求出解即可。
Q3.2 这次约束条件中既有不等式也有等式【我们把它称作 primal optimization problem，待会儿还会用到
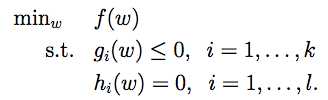
A3.2
STEP1：作广义lagrange函数
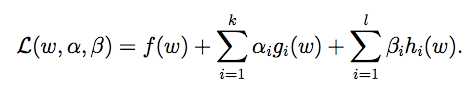（α,β是求解用的参数）
STEP2：定义
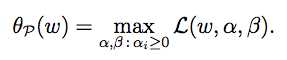即求L的最大值，其中α,β为变量，且a[i]>=0
由上式和约束条件可以得出：
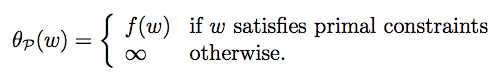【证明：设存在w‘使得gi(w‘)>0，那么就可以取a[i]为无穷大，使得L的值无穷大（反正θp(w)取的是L的最大值）
那么原问题(满足约束的情况下求f(w)的最小值)就转化成了求θp(w)的最小值
STEP3：求对偶问题
设上面的问题（求θp(w)的最小值）是问题p*，即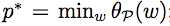
上面的一坨先边儿靠，来看另一个问题：令
//这里的D代表dual，即对偶
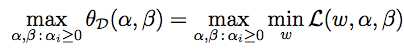//令这一坨等于d*，就是p*的对偶问题
结合之前θp(w)的定义式可以发现，d*和p*的不同实际上就是把前面max和min的顺序掉了个个儿
然而有一个定理：总是max[min(...)]<=min[max(...)]。因此
虽然这看起来并没有什么卵用，然而在某些特殊条件下其实是可以d*=p*的。这样对偶问题d*的解也就是p*的解了。而且大多数情况下，对偶问题解决起来更容易一些。
STEP4：临门一脚
设：
1) f和gi都是凸函数
2) hi是仿射函数（即 hi(w)=ai^T(w)+bi）
3) gi是严格可执行的（存在w，使得对于所有的i，都满足gi(w)<0。即不仅小于等于号成立而且小于号也可能成立）
若这些假设成立，那么存在w*,α*,β*，这里w*是原问题p*(primal problem)的解，同时α*,β*是对偶问题d*的解。即
另外，w*,α*,β*满足 Karush-Kuhn-Tucker (KKT) conditions ：
【其中中间的等式(5)又被称为KKT dual complementarity condition (KKT互补条件) 】
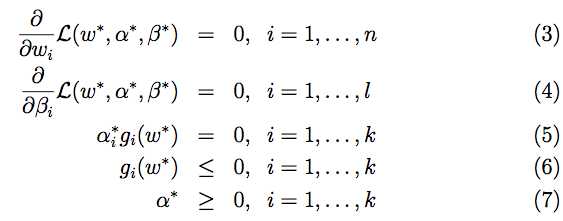
若w*,α*,β*满足KKT条件，那么它们同时是原问题和对偶问题的解。这样问题就解决啦~
标签：
原文地址：http://www.cnblogs.com/pdev/p/4621833.html
