标签:dearboys puzzle poj 2308 dfs+bfs 搜索
|
Language:
Dearboy‘s Puzzle
Description
Dearboy is a game lover. Recently, he loves playing the game Lian Lian Kan. This game is played on a board with N*M grids, and lots of cards are put on the board in the grids. You should find a pair of the same cards, if not more than three segments can link
this pair without passing any other cards, you can take this pair away from the board. (You may be puzzled about the meaning of not more than 3 segments, just refer to the figure below, in which we express some allowable links). Continue the process above,
if you can clear all the cards, you win the game, otherwise you lose it.
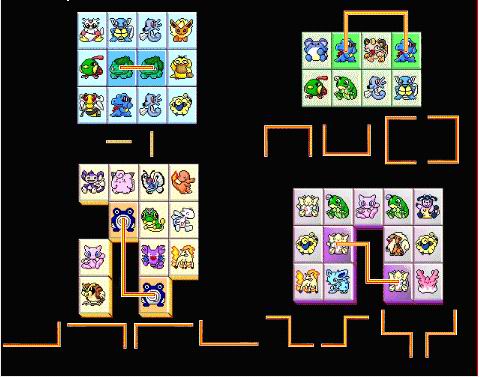 If you have played this game, you may know that sometimes the game has no solution and you are sure to lose. Dearboy is very boring about the games without solutions, so he asks you, a famous programmer, to tell him whether he can win the giving game phase or not. Input
The input consists of multiple test cases. The first line of each test case contains two integers N and M (2 <= N, M <= 10), which denote the sizes of the game board. The next N lines give the board layout, with each line containing M characters. A character
is one of the following: ‘*’ (an empty position), ‘A’, ‘B’, ‘C’, ’D’ (the cards, which imply that there are at most 4 different kinds of cards). Different letters represent different cards. The number of same cards may be odd, and there may be more than one
pair of the same cards.
The input is terminated with two 0‘s. This test case shoud not be processed. Output
For each test case, print in one line "yes" if Dearboy can win the game, "no" otherwise.
Sample Input 6 8 ******** *A**C*** **B***** ***B*D** ****D*** ******** 2 2 AB BA 6 8 ***A**** *A**C*** **B***C* ***B*D** ****D*** ******** 0 0 Sample Output no no yes Source
POJ Monthly,Wang Yijie
|
题意:连连看游戏,给定一个局面判断最后能不能消完。
思路:用dfs来确定消去哪一个格子(x,y),在dfs中进行bfs,看(x,y)周围有多少格子可以和(x,y)相消,找到之后再用dfs枚举与哪一个相消或者当前(x,y)不消。
注意一个剪枝,存在下面这种情况的肯定不符合题意:
*********
***AB***
***BA***
*********
另外,注意题意的消去方法,连线最多只转两个弯。
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <string>
#include <map>
#include <stack>
#include <vector>
#include <set>
#include <queue>
#pragma comment (linker,"/STACK:102400000,102400000")
#define maxn 1005
#define MAXN 2005
#define mod 1000000009
#define INF 0x3f3f3f3f
#define pi acos(-1.0)
#define eps 1e-6
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
#define FRE(i,a,b) for(i = a; i <= b; i++)
#define FREE(i,a,b) for(i = a; i >= b; i--)
#define FRL(i,a,b) for(i = a; i < b; i++)
#define FRLL(i,a,b) for(i = a; i > b; i--)
#define mem(t, v) memset ((t) , v, sizeof(t))
#define sf(n) scanf("%d", &n)
#define sff(a,b) scanf("%d %d", &a, &b)
#define sfff(a,b,c) scanf("%d %d %d", &a, &b, &c)
#define pf printf
#define DBG pf("Hi\n")
typedef long long ll;
using namespace std;
struct Node
{
int x,y,turn,w,d; //turn是走到当前(x,y)处已经转了多少个弯,d是(x,y)是有上一步哪个方向来的
};
int dir[4][2]={1,0,0,1,0,-1,-1,0};
int mp[11][11],num[4];
int n,m;
char str[11];
bool flag;
bool isok(int x,int y)
{
if (x>=0&&x<n&&y>=0&&y<m) return true;
return false;
}
bool isOK()
{
for (int i=0;i<n;i++)
{
for (int j=0;j<m;j++)
{
if (mp[i][j]!=-1&&mp[i][j+1]!=-1&&num[mp[i][j]]==num[mp[i][j+1]]&&num[mp[i][j]]==2)
{
if (mp[i][j]==mp[i+1][j+1]&&mp[i][j+1]==mp[i+1][j])
return true;
}
}
}
return false;
}
void bfs(int x,int y,int v,int s[25][2],int &nn)
{
nn=0;
queue<Node>Q;
Node st,now;
st.x=x; st.y=y; st.w=-1; st.turn=0; st.d=-1;
bool vis[11][11];
memset(vis,false,sizeof(vis));
vis[x][y]=true;
Q.push(st);
while (!Q.empty())
{
st=Q.front();Q.pop();
if (st.w==v)
{
s[nn][0]=st.x; //记录下找到的可以相消的格子的坐标
s[nn++][1]=st.y;
continue;
}
for (int i=0;i<4;i++)
{
now.x=st.x+dir[i][0];
now.y=st.y+dir[i][1];
if (isok(now.x,now.y)&&!vis[now.x][now.y])
{
if (mp[now.x][now.y]!=-1&&mp[now.x][now.y]!=v) continue;
if (st.d==i||st.d==-1)
now.turn=st.turn;
else
now.turn=st.turn+1;
if (now.turn<=2)
{
now.w=mp[now.x][now.y];
now.d=i;
vis[now.x][now.y]=true;
Q.push(now);
}
}
}
}
}
void dfs(int cnt)
{
if (flag) return ;
if (cnt==0)
{
flag=true;
return;
}
if (isOK()) return ; //剪枝
for (int i=0;i<n;i++)
{
for (int j=0;j<m;j++)
{
if (mp[i][j]!=-1)
{
int s[25][2];
int sum;
int v=mp[i][j];
bfs(i,j,v,s,sum);
num[v]-=2;
mp[i][j]=-1;
for (int k=0;k<sum;k++)
{
int x=s[k][0];
int y=s[k][1];
mp[x][y]=-1;
dfs(cnt-2);
mp[x][y]=v;
}
num[v]+=2;
mp[i][j]=v;
}
}
}
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("C:/Users/asus1/Desktop/IN.txt","r",stdin);
#endif
int i,j;
while (scanf("%d%d",&n,&m))
{
if (n==0&&m==0) break;
flag=false;
mem(num,0);
mem(mp,-1);
int all=0;
for (i=0;i<n;i++)
{
scanf("%s",str);
for (j=0;j<m;j++)
{
if (str[j]=='*') mp[i][j]=-1;
else if (str[j]=='A'){
num[0]++;
mp[i][j]=0;
all++;
}
else if (str[j]=='B')
{
num[1]++;
mp[i][j]=1;
all++;
}
else if (str[j]=='C')
{
num[2]++;
mp[i][j]=2;
all++;
}
else{
num[3]++;
mp[i][j]=3;
all++;
}
}
}
if (num[0]%2||num[1]%2||num[2]%2||num[3]%2) //存在奇数时肯定不合要求
{
pf("no\n");
continue;
}
dfs(all);
if (flag)
pf("yes\n");
else
pf("no\n");
}
return 0;
}
|
Language:
Dearboy‘s Puzzle
Description
Dearboy is a game lover. Recently, he loves playing the game Lian Lian Kan. This game is played on a board with N*M grids, and lots of cards are put on the board in the grids. You should find a pair of the same cards, if not more than three segments can link
this pair without passing any other cards, you can take this pair away from the board. (You may be puzzled about the meaning of not more than 3 segments, just refer to the figure below, in which we express some allowable links). Continue the process above,
if you can clear all the cards, you win the game, otherwise you lose it.
 If you have played this game, you may know that sometimes the game has no solution and you are sure to lose. Dearboy is very boring about the games without solutions, so he asks you, a famous programmer, to tell him whether he can win the giving game phase or not. Input
The input consists of multiple test cases. The first line of each test case contains two integers N and M (2 <= N, M <= 10), which denote the sizes of the game board. The next N lines give the board layout, with each line containing M characters. A character
is one of the following: ‘*’ (an empty position), ‘A’, ‘B’, ‘C’, ’D’ (the cards, which imply that there are at most 4 different kinds of cards). Different letters represent different cards. The number of same cards may be odd, and there may be more than one
pair of the same cards.
The input is terminated with two 0‘s. This test case shoud not be processed. Output
For each test case, print in one line "yes" if Dearboy can win the game, "no" otherwise.
Sample Input 6 8 ******** *A**C*** **B***** ***B*D** ****D*** ******** 2 2 AB BA 6 8 ***A**** *A**C*** **B***C* ***B*D** ****D*** ******** 0 0 Sample Output no no yes Source
POJ Monthly,Wang Yijie
|
版权声明:本文为博主原创文章,未经博主允许不得转载。
Dearboy's Puzzle (poj 2308 搜索 dfs+bfs)
标签:dearboys puzzle poj 2308 dfs+bfs 搜索
原文地址:http://blog.csdn.net/u014422052/article/details/46778893