标签:
给定平面上N个点的坐标,找出距离最近的两个点。
我们不妨先看一看一维的情况:在一个包含N个数的数组中,如何快速找出N个数中两两差值的最小值?一维的情况相当于所有的点都在一条直线上。虽然是一个退化的情况,但还是能从中得到一些启发。
数组中共包含N个数,我们把它们两两之间的差值都求出来,那样就不难得出最小的差值了。这样一个直接的想法,时间复杂度为O(N2)。具体代码如下:
1 package chapter2shuzizhimei.findminpointspair; 2 /** 3 * 寻找最近点对 4 * 【解法一】 5 * @author DELL 6 * 7 */ 8 public class FindMinPair1 { 9 public static double minDifference(double a[]){ 10 int n = a.length; 11 if(n<2) 12 return 0; 13 double minDiff = Math.abs(a[0]-a[1]); //记录最短距离 14 for(int i=0;i<n;i++){ 15 for(int j=i+1;j<n;j++){ 16 double diff = Math.abs(a[i]-a[j]); 17 if(diff<minDiff){ 18 minDiff = diff; 19 } 20 } 21 } 22 return minDiff; 23 } 24 public static void main(String[] args) { 25 double a[]={1,6,4,2,8,16}; 26 System.out.println("最短距离为:"+minDifference(a)); 27 28 } 29 30 }
程序运行结果如下:
最短距离为:1.0

具体代码如下:
1 package chapter2shuzizhimei.findminpointspair; 2 /** 3 * 寻找最近点对 4 * 【解法二】先排序 5 * @author DELL 6 * 7 */ 8 public class FindMinPair2 { 9 //快速排序的一次划分 10 public static int partition(double a[],int first, int last){ 11 double temp = a[first]; 12 int i = first,j = last; 13 while(i<j){ 14 while(i<j&&a[j]>=temp){ 15 j--; 16 } 17 if(i<j) 18 a[i] = a[j]; 19 while(i<j&&a[i]<=temp){ 20 i++; 21 } 22 if(i<j) 23 a[j] = a[i]; 24 } 25 a[i] = temp; 26 return i; 27 } 28 //快速排序 29 public static void quickSort(double a[],int first, int last){ 30 if(first>=last) 31 return; 32 int i = partition(a,first,last); 33 quickSort(a,first,i-1); 34 quickSort(a,i+1,last); 35 } 36 //找最小距离 37 public static double minDifference(double a[]){ 38 int n = a.length; 39 if(n<2) 40 return 0; 41 quickSort(a, 0, n-1); //从小到大排序 42 double minDiff = a[1]-a[0]; //记录最短距离 43 for(int i=1;i<n-1;i++){ 44 double diff = a[i+1]-a[i]; 45 if(diff<minDiff){ 46 minDiff = diff; 47 } 48 } 49 return minDiff; 50 } 51 public static void main(String[] args) { 52 double a[]={1,6,4,2,8,16}; 53 System.out.println("最短距离为:"+minDifference(a)); 54 55 } 56 57 }
程序运行结果如下:
最短距离为:1.0
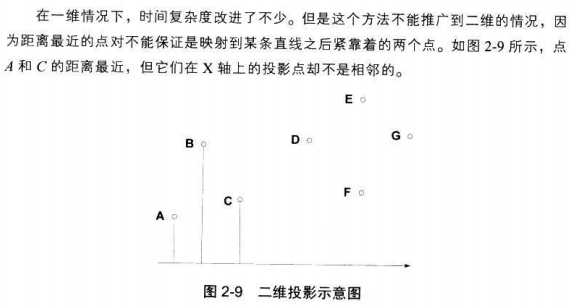


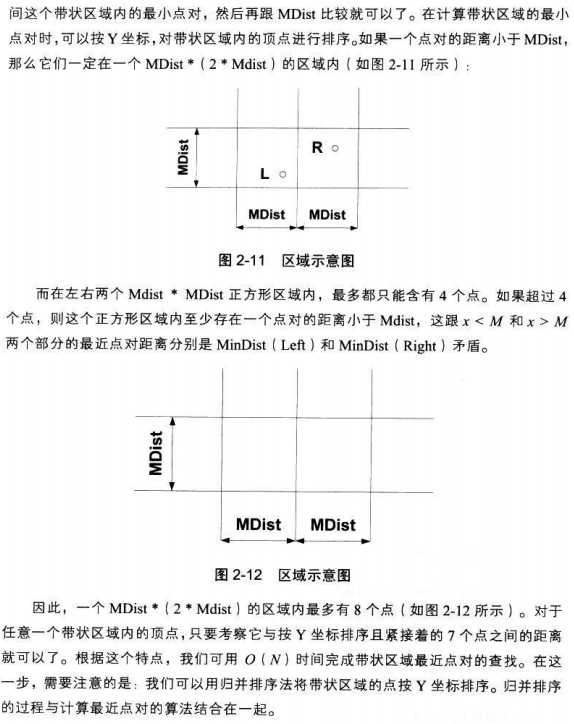



标签:
原文地址:http://www.cnblogs.com/gaopeng527/p/4625177.html