标签:
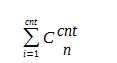 )%mod
)%mod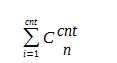 %(mod-1))%mod
%(mod-1))%mod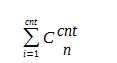 。
。
1 #include<cstdio> 2 #include<cstring> 3 #include<cmath> 4 #include<algorithm> 5 6 #define mo 999911659 7 8 typedef long long ll; 9 10 using namespace std; 11 12 int mod[5]={0,2,3,4679,35617}; 13 14 ll w[5],fac[5][36001]; 15 16 ll Qvod(ll x,ll k,ll mod) 17 { 18 ll ans=1; 19 while(k!=0) 20 { 21 if(k&1)ans=ans*x%mod; 22 x=x*x%mod; 23 k>>=1; 24 } 25 return ans; 26 } 27 28 ll C(ll x,ll k,ll m) 29 { 30 if(x<k)return 0; 31 return fac[m][x]*Qvod(fac[m][k]*fac[m][x-k],mod[m]-2,mod[m])%mod[m]; 32 } 33 34 ll Lucas(ll x,ll k,int m) 35 { 36 if(x==0)return 1; 37 return Lucas(x/mod[m],k/mod[m],m)*C(k%mod[m],x%mod[m],m)%mod[m]; 38 } 39 40 ll x,y; 41 42 void exgcd(ll n,ll m) 43 { 44 if(m==0){x=1,y=0;return;} 45 exgcd(m,n%m); 46 ll t=x;x=y,y=t-n/m*y; 47 } 48 49 ll solve() 50 { 51 ll ans=0; 52 for(int i=1;i<=4;i++) 53 { 54 ll sb=(mo-1)/mod[i]; 55 exgcd(sb,mod[i]); 56 ans=(ans+x*sb*w[i])%(mo-1); 57 } 58 if(ans<=mo-1)ans+=(mo-1); 59 return ans; 60 } 61 62 int main() 63 { 64 for(int i=1;i<=4;i++) 65 { 66 fac[i][0]=1; 67 for(int j=1;j<=mod[i];j++) 68 fac[i][j]=fac[i][j-1]*j%mod[i]; 69 } 70 int n,g; 71 scanf("%d%d",&n,&g); 72 if(g==mo){printf("0");return 0;} 73 g%=mo; 74 for(int i=1;i<=sqrt(n);i++) 75 { 76 if(n%i==0) 77 { 78 int tmp=n/i; 79 for(int j=1;j<=4;j++){ 80 if(tmp!=i)w[j]=(w[j]+Lucas(tmp,n,j)); 81 w[j]=(w[j]+Lucas(i,n,j))%mod[j]; 82 } 83 } 84 } 85 printf("%lld",Qvod(g,solve(),mo)); 86 return 0; 87 }
【数学/扩展欧几里得/Lucas定理】BZOJ 1951 :[Sdoi 2010]古代猪文
标签:
原文地址:http://www.cnblogs.com/tuigou/p/4628482.html