标签:
本文转载地址:http://www.cnblogs.com/zuoxiaolong/p/computer11.html
2.6我们进行了二进制整数运算的最后一役,本次LZ将和各位一起进入浮点数的世界,这里没有无符号,没有补码,但是有各种各样的惊奇。倘若你真正的进入了浮点数的世界,一定会发现它原来是这么有意思,而不是像之前一样,觉得了解浮点数的内容没什么用,只要会简单的使用就行了。当然,这其中也可能有部分猿友是觉得这部分内容太难,而对它失去了学习的兴趣。
就像之前的LZ一样,曾经对IEEE标准望而却步,不过相信这几章浮点数的介绍会让你有种顿悟的感觉。
整数运算虽然能解决计算机当中有关信息的很大一部分储存、运算等功能,但却是仍然不够的。否则假设我们要做一个超市的库存管理系统,那么所有商品的价格都只能是整数,这是不是让你难以接受呢。
因此有时候我们需要更精确的数值表示,这就需要浮点数出场了。对于浮点数的表示以及运算规则,在以前是各个计算机制造商各自有一套自己的标准,这给程序的可移植性造成了很大的困扰。
有需求就有创新,最终在1985年左右,浮点数标准IEEE754就应运而生了。它就像一代秦始皇一样,一统浮点数世界。秦始皇统一了文字、货币等,而IEEE754统一了浮点数的标准。
浮点数不仅仅是为了让数值的表示更加精确,也是为了表示一些整数无法达到的数字,比如一些接近于0的数字,或者一些非常大的数值。因此浮点数对于计算机的意义,可以说是相当之大。
尽管我们本章的主要内容应该是IEEE标准,不过我们先来看看二进制是如何表示小数的,这有助于我们理解浮点数的表示。如果是一个十进制小数,相信各位都再熟悉不过了,对于12345.6789来说,它的值是由下列式子得到的。
12345.6789 = 1 * 104 + 2 * 103 + 3 * 102 + 4 * 101 + 5 * 100 + 6 * 10-1 + 7 * 10-2 + 8 * 10-3 + 9 * 10-4
这对我们来说应该是常识,那么对于二进制小数也是类似的,考虑这样一个小数10010.1110,它的值则可以由以下式子得到。
10010.1110 = 1 * 24 + 0 * 23 + 0 * 22 + 1 * 21 + 0 * 20 + 1 * 2-1 + 1 * 2-2 + 1 * 2-3 + 0 * 2-4 = 16 + 2 + 1/2 + 1/4 + 1/8 = 18.875
从这个角度来看,二进制小数其实与十进制小数是一样的计算方式,只是这里是2的整数次幂而已。
在书中给出了二进制小数的公式,对于一个形式为bm....b0.b-1....b-n的二进制小数b来说,它的值为以下计算方式。

这里需要提醒的是,二进制小数不像整数一样,只要位数足够,它就可以表示所有整数。二进制小数无法精确的表示任意小数,比如最简单的,十进制小数0.3这样一个小数,二进制是无法精确的表示它的。
IEEE标准采用类似于科学计数法的方式表示浮点小数,即我们将每一个浮点数表示为 V = (-1)s * M * 2E 。
这其中s为符号位,为0时为正,为1时为负。M为尾数,是一个二进制小数,它的范围是0至1-ε,或者1至2-ε(ε的值一般是2-k次方,其中设k > 0)。E为阶码,是一个二进制整数,可正可负,为了给尾数加权。
浮点格式分为两种,一种是单精度,一种是双精度。单双精度分别对应于编程语言当中的float和double类型。其中float是单精度的,采用32位二进制表示,其中1位符号位,8位阶码以及23位尾数。double是双精度的,采用64位二进制表示,其中1位符号位,11位阶码以及52位尾数。
从上面的位数上就能看出,双精度浮点数所表示的范围将远远大于单精度浮点数。针对阶码E的值,浮点数的值可以分为三种不同的情况,分别是规格化的,非规格化的以及特殊值,这三种情况就是浮点数的奥义所在了。
下面LZ首先给出一个书中对于单精度的三种情况的图示描述,分别是1、2、3,其中3也就是特殊值又分了两种情况3a和3b。各位猿友可以先看一下图示的描述,接下来我们再一一具体分析。
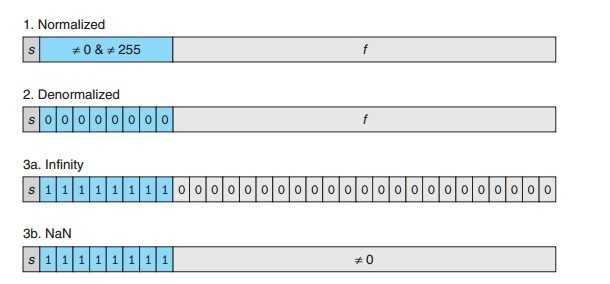
规格化的浮点数是上述的第1种情况,对于单精度来说,也就是阶码位不为0且不为255的这种情况。
在此范围内的浮点数,阶码会被转换成一个“偏置”后的有符号数。“偏置”的含义就是在原有的值的基础上加上一个偏移量,对于阶码位数为k的情况来说,偏移量Bias = 2k-1-1。假设e是阶码的无符号数值,那么真实的阶码E = e - Bias。举个例子,假设阶码位数为8,则Bias = 127。由于8位阶码下的规格化的浮点数的阶码范围是1至254,因此真实阶码的范围则为-126至127。
对于尾数的解释,则是一个小于1的小数或者0。也就是假设尾数位表示为fn-1...f0,则f的值为0.fn-1...f0。这只是尾数的值,当计算浮点数数值的时候,会在尾数值的基础上加1,也就是真实的尾数M = 1 + f。相当于我们省掉了1位二进制,形成了浮点数表示的约定,默认尾数的值还有一个最高位的1。
非规格化的浮点数对应图中的第2种情况,也就是阶码全为0的时候。
按照上面规格化的阶码求值方式来说,非规格化的阶码值应该固定在-Bias这个值上面。不过这里有一个小技巧,我们设定阶码的值E = 1 - Bias。这样做是为了能够平滑的从非规格化的浮点数过渡到规格化的浮点数,有关这一点后面我们再详细看。
对于尾数的解释,非规格化的方式与规格化不同,它不会对尾数进行加1的处理,也就是说,真实的尾数M = f。这是为了能够表示0这个数值,否则的话尾数总是大于1,那么无论如何都将得不到0这个数值。
非规格化的浮点数除了可以表示0以外,它还有一个作用,就是可以表示接近于0的数值。另外,在浮点数当中,0的表示有两种,一种是位表示全部为0,则为+0.0。还有一种则是符号位为1,其余全为0,此时为-0.0。
特殊值则对应图中的3a和3b这两种情况,也就是阶码全为1的时候。
在阶码全为1时,如果尾数位全为0,则表示无穷大。符号位为0则表示正无穷大,相反则表示负无穷大。倘若尾数位不全为0时,此时则表示NaN,表示不是一个数字。这一点在Javascript当中有一个相关的函数与这个NaN的含义有点类似,它的作用是用来判断一个参数是否是一个数字。
下面我们来讨论一下上面三种浮点数情况的取值范围,我们假设一个浮点数有1个符号位s,k个阶码位以及n个尾数位。下面我们讨论这样一个浮点数在各个情况下的一些取值范围。
在谈论取值范围之前,首先要说明两点,第一点是由于特殊值的特殊性,它没有取值范围这一概念,因此不在我们的讨论范围之内。第二点是,由于浮点数在正负的区间内是一一对应的,因此我们将忽略符号位对取值范围的影响,我们只讨论符号位为0的情况。
对于非规格化的浮点数来说,由于阶码固定为k个0,因此真实阶码都为 E = 1 - (2k-1 - 1) = 2 - 2k-1。那么我们可以得到下面几个重要的取值。
1、当尾数为n个0时,此时的值为+0.0。
2、当尾数为最低位为1,其余全为0时,此时的值为最小的非0值。它此时的尾数 M = f = 2-n,因此此时的值为 2-n * 22 - 2k-1 = 2-n+2 - 2k-1。
3、当尾数为n个1时,此时的值为最大的非规格化的值。它此时的尾数 M = f = 1 - 2-n,因此此时的值为 (1 - 2-n) * 22 - 2k-1。(可能是印刷问题或是作者的笔误,这一个值在书中写错了,正确的值应该是LZ给出的这个,在书中给出的这一值为 (1 - 2-n) * 2-n + 2 - 2k-1)
对于规格化的浮点数来说,同样有三个比较重要的取值。
1、当阶码为最低位为1,其余全为0,尾数为n个0时,此时的值为最小的规格化的值。它此时的阶码恰好与非规格化的阶码相同,都为E = 2 - 2k-1。而它的尾数值则很好计算,由于尾数全部为0,则M = 1 + f = 1。因此此时的值为22 - 2k-1。
这里需要特别提一下,对于最小的规格化的值来说,它的阶码位刚好与非规格化的值的阶码位相等,这正是因为我们将非规格化的阶码位取为1-Bias而不是-Bias的功劳。由于二者的阶码相同,而二者的尾数刚好相差2-n(2-n刚好是n位尾数时所能表示的最小精度),这正好完成了非规格化的值到规格化的值的平滑过渡。也可以看出,最小的规格化的值刚好比最大的非规格化的值大一点。
2、当阶码为最高位为0,其余全为1,尾数为n个0时,此时的值为1。因为在偏置之后,阶码E = 0 ,而尾数M = 1 + f = 1。
3、当阶码为最低位为0,其余全为1,尾数为n个1时,此时的值为最大的规格化的值。此时的阶码E = 2k-1-1,尾数M = 2 - 2-n。因此此时的值为
(2 - 2-n) * 2-1 + 2k-1,也可以化简一下为(1 - 2-n-1) * 22k-1。
书中给出了单双精度中上述六种值的表示方式以及它们的值,我们根据上面的公式可以算出这些值,LZ这里就不给大家一一来算了。这里直接给出这个图表,让各位猿友一观而已。(其中exp是阶码的位表示,frac是尾数的位表示)
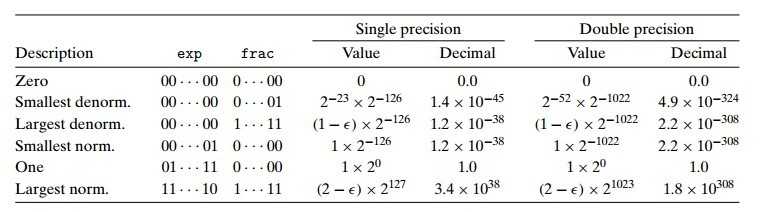
可以看出,这里能表示的值范围是相当大的,这对于一些需要大数值的科学研究程序或者一些应用程序来说,都是非常需要的。
这里LZ和各位一起来看一个书中有意思的练习题,题目的原文如下。
题目:对于一种具有n位小数的浮点格式,给出不能准确描述的最小正整数的公式(因为想要准确表示它可能需要n+1位小数)。假设阶码字段长度k足够大,可以表示的阶码范围不会限制这个问题。
分析:首先可以排除非规格化里的数值范围,因为那些值全部都小于1。在考虑规格化的数值范围里,倘若需要n+1位小数表示,并且是最小的小数的话,则应该是由n个0和最低位的1个1组成。也就是此时的尾数M = 1 + f = 1 + 2-n-1,此时我们使用阶码抵消掉小数位,则取阶码为2n+1,因此最后的值为2n+1+1。
我们来举个例子,考虑最简单的,比如当n为1时,则根据上面的式子可以算出这个值为5。此时我们可以将尾数的所有值都列出来,分别为0、1/2、1、3/2。可以看出无论阶码取多少,都是不可能表示5、6、7、9等等这些数字的(任何一个大于等于5又不是2的整数次幂的值都不能表示),而像1、2、3、4这些都是可以表示的,因此最小的不能准确描述的值就是5。
本次我们主要介绍了IEEE浮点标准,本章的难度相对来说没有上一章的难度高,因此各位猿友看起来应该不会太费力。下一章将是2.X系列的最后一章,其中主要包括浮点数的舍入以及运算部分的内容。
深入理解计算机系统(2.7)---二进制浮点数,IEEE标准(重要)
标签:
原文地址:http://www.cnblogs.com/hthuang/p/4629557.html