标签：
维数灾难
给定如下分类问题：
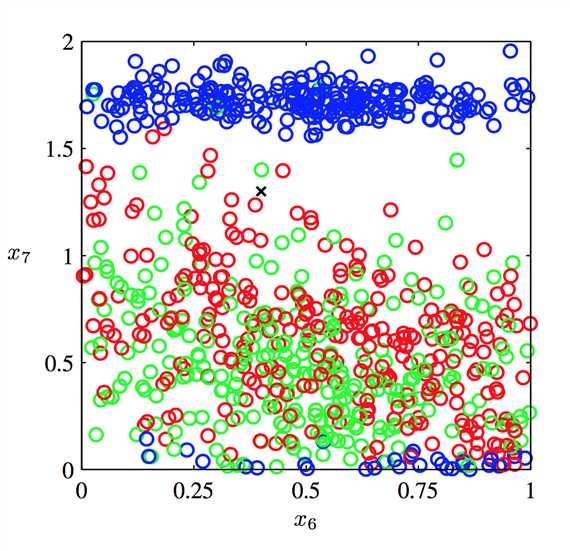
其中x6和x7表示横轴和竖轴（即两个measurements），怎么分？
方法一（simple）：
把整个图分成；16个格，当给定一个新的点的时候，就数他所在的格子中，哪种颜色的点最多，最多的点就是最有可能的。
如图：
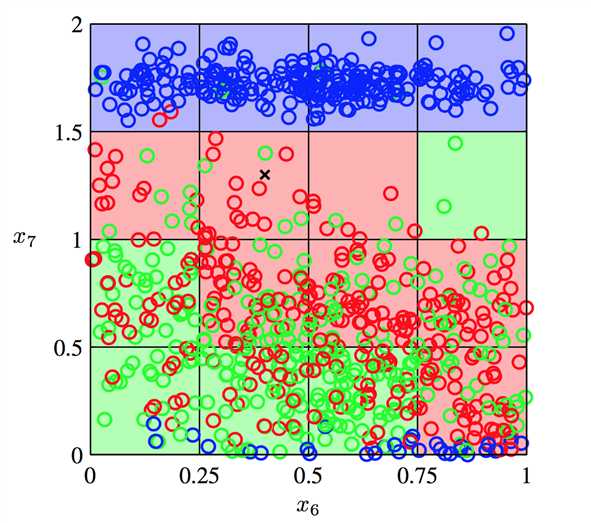
显然，这种方法是有缺陷的：
例子给出的是2维的，那么3维的话，就是一个立体的空间，如下图所示：
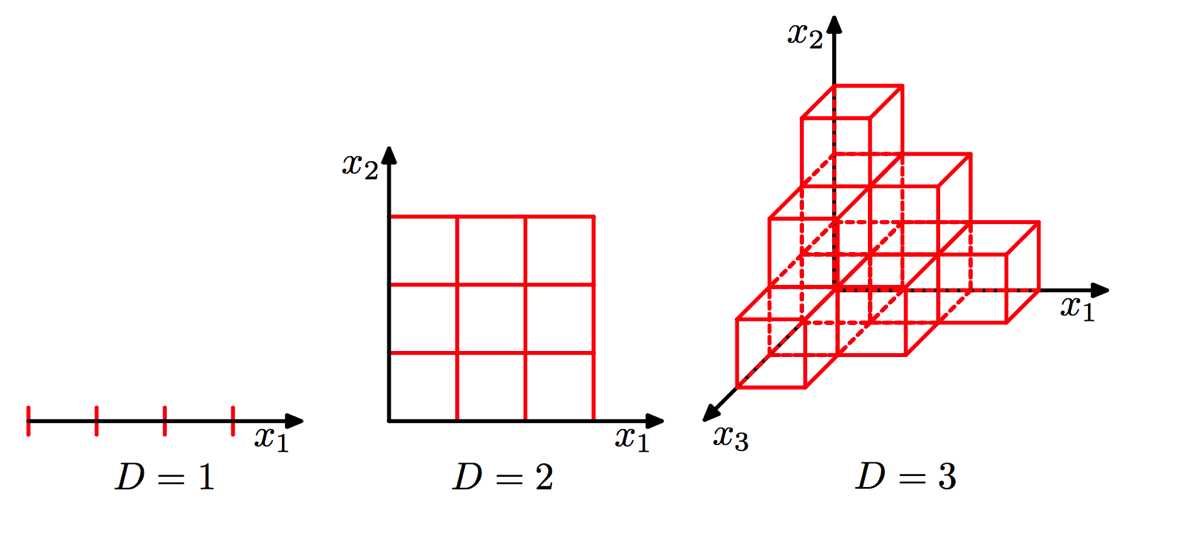
因为我们生活在3维的世界里，所以我们很容易接受3维。比如，我们考虑一个在D维环境下，半径为1和半径为1-
的球体的容积之差：
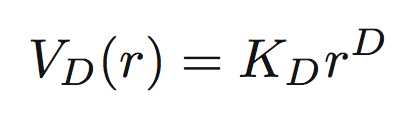
他们的差即为：
volume fraction＝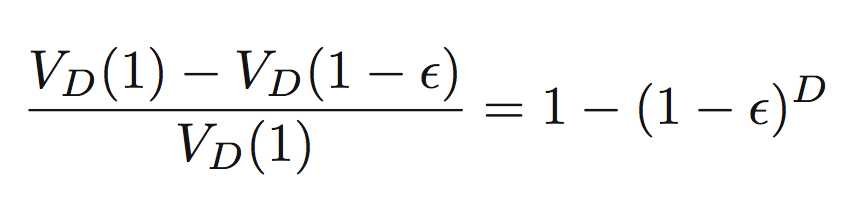
根据式子我们可以看出，volume fraction越小，即越接近于0，则说明两者相差越小。结果是：
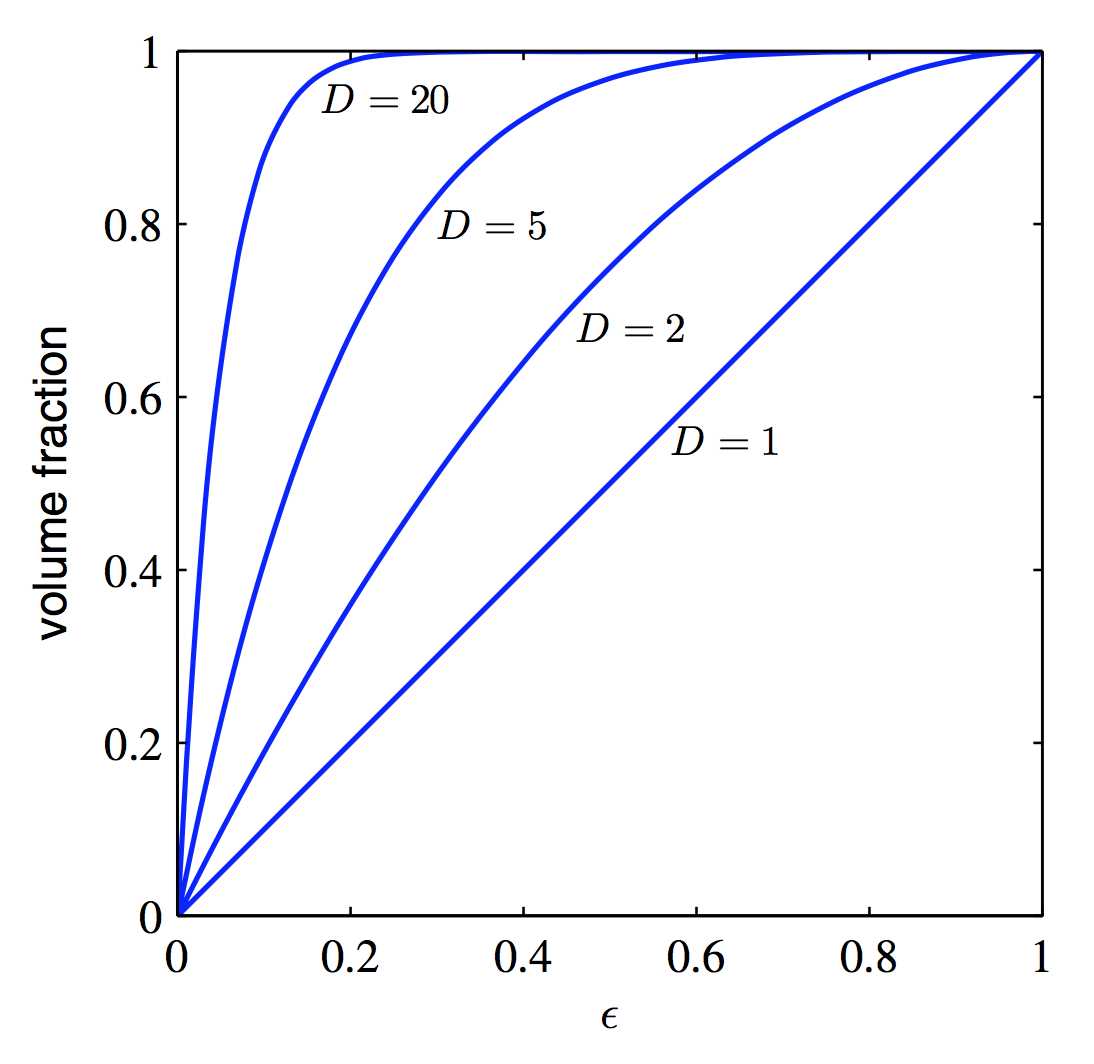
可以发现，维数越大，一定时，他们的差异也就越大。维数越高，附着在表层的容积也就越大。
尽管维数灾难会给我们带来难度，但是并不影响我们找到解决高维问题的解决方案。原因是：
1.现实生活中的数据大都有部分的重要的变量；
2.现实的数据往往比较平滑，小的改变不会引起巨大的变化。
【PRML读书笔记-Chapter1-Introduction】1.4 The Curse of Dimensionality
标签：
原文地址：http://www.cnblogs.com/XBWer/p/4631102.html
