大家好,我是小Hi和小Ho的小伙伴Nettle,从这个星期开始由我来完成我们的Weekly。
新年回家,又到了一年一度大龄剩男剩女的相亲时间。Nettle去姑姑家玩的时候看到了一张姑姑写的相亲情况表,上面都是姑姑介绍相亲的剩男剩女们。每行有2个名字,表示这两个人有一场相亲。由于姑姑年龄比较大了记性不是太好,加上相亲的人很多,所以姑姑一时也想不起来其中有些人的性别。因此她拜托我检查一下相亲表里面有没有错误的记录,即是否把两个同性安排了相亲。
OK,让我们愉快的暴力搜索吧!
才怪咧。
对于拿到的相亲情况表,我们不妨将其转化成一个图。将每一个人作为一个点(编号1..N),若两个人之间有一场相亲,则在对应的点之间连接一条无向边。(如下图)
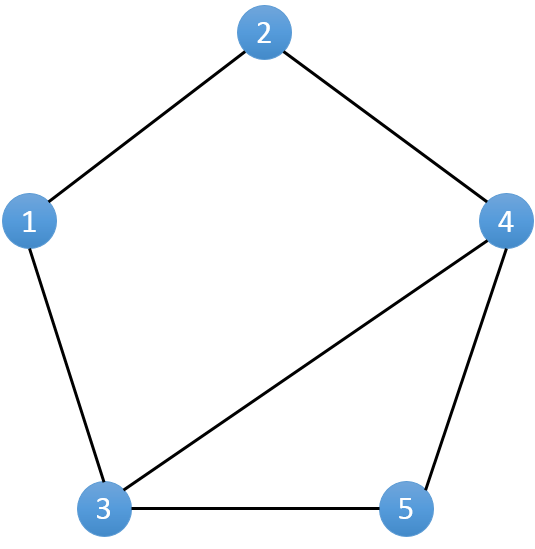
因为相亲总是在男女之间进行的,所以每一条边的两边对应的人总是不同性别。假设表示男性的节点染成白色,女性的节点染色黑色。对于得到的无向图来说,即每一条边的两端一定是一白一黑。如果存在一条边两端同为白色或者黑色,则表示这一条边所表示的记录有误。
由于我们并不知道每个人的性别,我们的问题就转化为判定是否存在一个合理的染色方案,使得我们所建立的无向图满足每一条边两端的顶点颜色都不相同。
那么,我们不妨将所有的点初始为未染色的状态。随机选择一个点,将其染成白色。再以它为起点,将所有相邻的点染成黑色。再以这些黑色的点为起点,将所有与其相邻未染色的点染成白色。不断重复直到整个图都染色完成。(如下图)

在染色的过程中,我们应该怎样发现错误的记录呢?相信你一定发现了吧。对于一个已经染色的点,如果存在一个与它相邻的已染色点和它的颜色相同,那么就一定存在一条错误的记录。(如上图的4,5节点)
到此我们就得到了整个图的算法:
接下来就动手写写吧!
第1行:1个正整数T(1≤T≤10)
接下来T组数据,每组数据按照以下格式给出:
第1行:2个正整数N,M(1≤N≤10,000,1≤M≤40,000)
第2..M+1行:每行两个整数u,v表示u和v之间有一条边
第1..T行:第i行表示第i组数据是否有误。如果是正确的数据输出”Correct”,否则输出”Wrong”
2 5 5 1 2 1 3 3 4 5 2 1 5 5 5 1 2 1 3 3 4 5 2 3 5
Wrong Correct
好久没写代码,,继续攒点模板!
AC代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int T;
int n, m;
const int maxn = 10005;
vector<int> G[maxn];
bool vis[maxn];
int f[maxn];
int bfs(int i) {
queue<int> que;
que.push(i);
vis[i] = true;
f[i] = 0;
while(!que.empty()) {
int e = que.front();
que.pop();
int d = G[e].size();
// cout << e << endl;
for(int i = 0; i < d; i ++) {
int t = G[e][i];
// cout << t << " ";
if(vis[t]) {
if(f[t] == f[e]) return 1;
}
else {
vis[t] = true;
f[t] = f[e] == 0 ? 1 : 0;
que.push(t);
}
}
// cout << endl;
}
return 0;
}
int fun() { //注意可能会有多个连通分量
for(int i = 1; i <= n; i ++) {
if(!vis[i]) {
if(bfs(i) == 1) return 1;
}
}
return 0;
}
int main() {
scanf("%d", &T);
while(T --) {
// for(int i = 0; i < maxn; i ++) G[i].clear();
scanf("%d %d", &n, &m);
for(int i = 0; i < m; i ++) {
int u, v;
scanf("%d %d", &u, &v);
G[u].push_back(v);
G[v].push_back(u);
}
memset(vis, false, sizeof(vis));
if(fun() == 1) {
printf("Wrong\n");
}
else printf("Correct\n");
// for(int i = 1; i <= n; i ++) {
// cout << f[i] << " ";
// }
for(int i = 1; i <= n; i ++) G[i].clear();
}
return 0;
}
版权声明:本文为博主原创文章,未经博主允许不得转载。
原文地址:http://blog.csdn.net/u014355480/article/details/46840907