标签:
来源:http://www.cnblogs.com/stonehat/p/3603267.html
在此,顶礼膜拜一下原文作者呵呵
我们知道整数n的位数的计算方法为:log10(n)+1
故n!的位数为log10(n!)+1
如果要求出n!的具体值,对很大的n(例如n=1000000)来说,计算会很慢,如果仅仅是求阶乘的位数,可以用斯特林(Stirling)公式求解
斯特林(Stirling)公式:
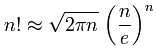
于是求n!的位数就是求log10((2*PI*n)^1/2*(n/e)^n)+1
即 1/2*log10(2*PI*n)+n*log10(n/e)+1
所以采用下面代码计算阶乘位数,会非常快
1 #define PI 3.141592654 2 #define E 2.71828182846 3 int l(int n) 4 { 5 int s=1; 6 if(n>3) 7 s=log10(2*PI*n)/2+n*log10(n/E)+1; 8 return s; 9 }
如果要计算阶乘的精确值,则可以采用下面代码。
1 /* 2 函数功能:计算并输出n 的阶乘 3 返回值:阶乘结果的位数 4 注意: 5 本程序直接输出n!的结果,需要返回结果请保留long a[] 6 需要 math.h 7 */ 8 9 int factorial(int n) 10 { 11 long a[10000]; 12 int i,j,l,c,m=0,w; 13 a[0]=1; 14 for(i=1;i<=n;i++) 15 { 16 c=0; 17 for(j=0;j<=m;j++) 18 { 19 a[j]=a[j]*i+c; 20 c=a[j]/10000; 21 a[j]=a[j]%10000; 22 } 23 if(c>0) {m++;a[m]=c;} 24 } 25 26 w=m*4+log10(a[m])+1; 27 printf("\n%ld",a[m]); 28 for(i=m-1;i>=0;i--) printf("%4.4ld",a[i]); 29 return w; 30 }
标签:
原文地址:http://www.cnblogs.com/huashanqingzhu/p/4639126.html