标签:
问题描述
Given an integer n, count the total number of digit 1 appearing in all non-negative integers less than or equal to n.
For example:
Given n = 13,
Return 6, because digit 1 occurred in the following numbers: 1, 10, 11, 12, 13.
解决思路
1. 遍历+计数法(可以转成字符串计数):超时;
2. 数学法:寻找规律。规律就是:
----------------------------------------------------------------------------------------------------------
写一个函数f(N),返回1到N之间出现的"1"的个数,比如f(12) = 5。
假设N = abcde,这里a,b,c,d,e分别是十进制数N的各个数位上的数字。如果要计算百位上出现1
的次数,将受3方面因素影响:百位上的数字,百位以下(低位)的数字,百位(更高位)以上的数字。
如果百位上的数字为0,则可以知道百位上可能出现1的次数由更高位决定,比如12 013,则可以知
道百位出现1的情况可能是100-199,1 100-1 199,……,11 100-11 199,一共有1 200个。也就是
由更高位数字(12) 决定,并且等于更高位数字(12)×当前位数(100)。
如果百位上的数字为1,则可以知道,百位上可能出现1的次数不仅受更高位影响,还受低位影响,
也就是由更高位和低位共同决定。例如12 113, 受更高位影响,百位出现1的情况是100-199,1 100
-1 199,……,11 100-11 199,一共有1 200个,和上面第一种情况一样,等于更高位数字(12)×当
前位数(100)。但它还受低位影响,百位出现1的情况是12 100-12 113,一共114个,等于低位数字
(113)+1。
如果百位上数字大于1(即为2-9),则百位上可能出现1的次数也仅由更高位决定,比如12 213,则
百位出现1的情况是:100-199,1 100-1 199,……,11 100-11 199,12 100-12 199,共1300个
,并且等于更高位数字+1(12+1)×当前位数(100)。
----------------------------------------------------------------------------------------------------------------
举个例子,三位数的话,如下图:
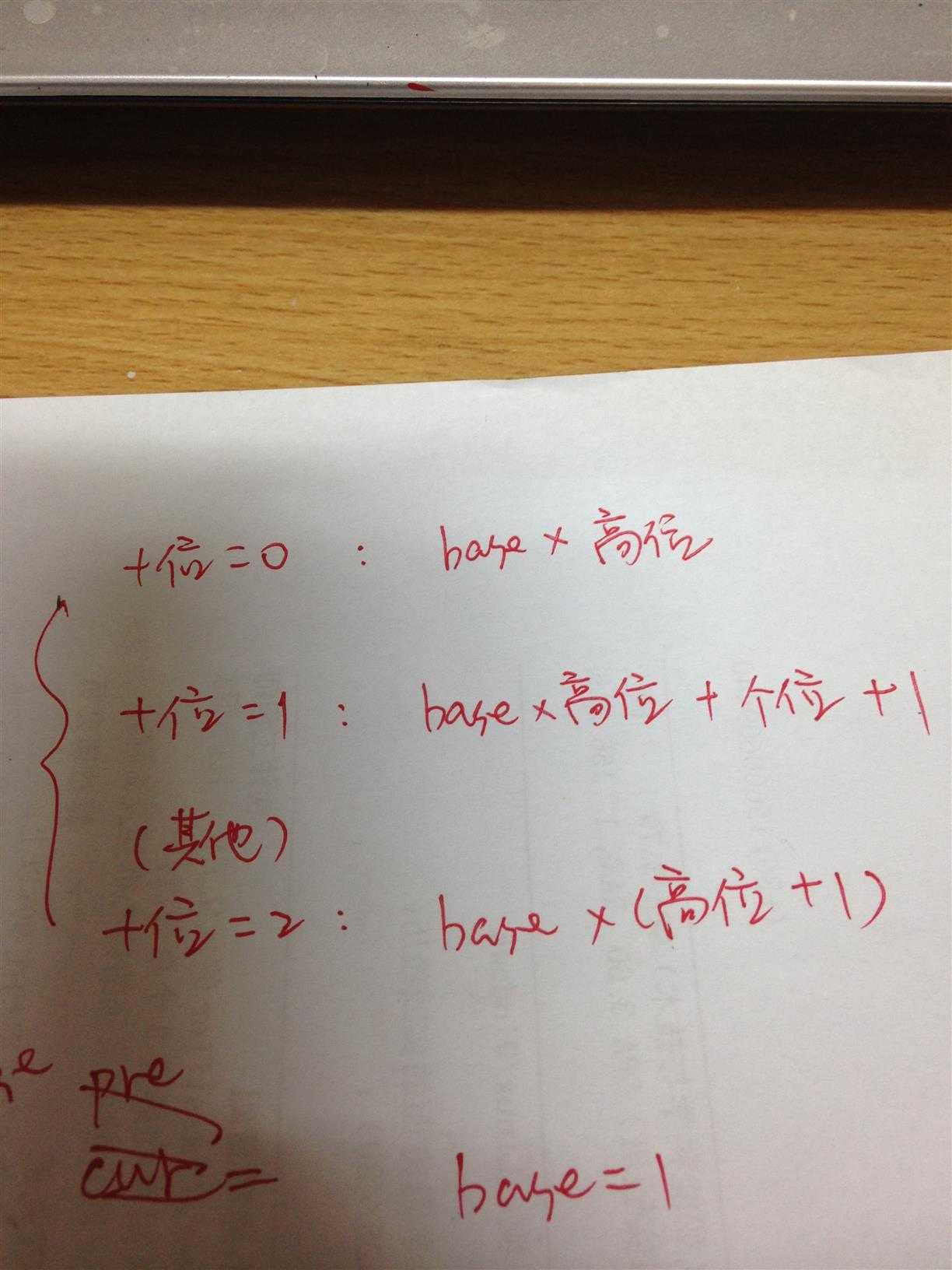
程序
第二种方法:
public class NumOfOnes {
public int countDigitOne(int n) {
long cnt = 0;
long base = 1;
while (n >= base) {
long low = n % base;
long cur = (n / base) % 10;
long high = n / (base * 10);
if (cur == 0) {
cnt += high * base;
} else if (cur == 1) {
cnt += base * high + low + 1;
} else {
cnt += base * (high + 1);
}
base *= 10;
}
return (int) cnt;
}
}
值得注意的是,需要使用long甚至更大位数的单位存储cnt,否则容易越界。
标签:
原文地址:http://www.cnblogs.com/harrygogo/p/4641548.html