标签:
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 1369 | Accepted: 542 |
Description
Input
Output
Sample Input
7 3 2 4 1 2 3 3 3 6 7 3 9 2 4 5 0 2 4 0 2 0 4 2 1 3 0 5 4 4
Sample Output
17
Hint
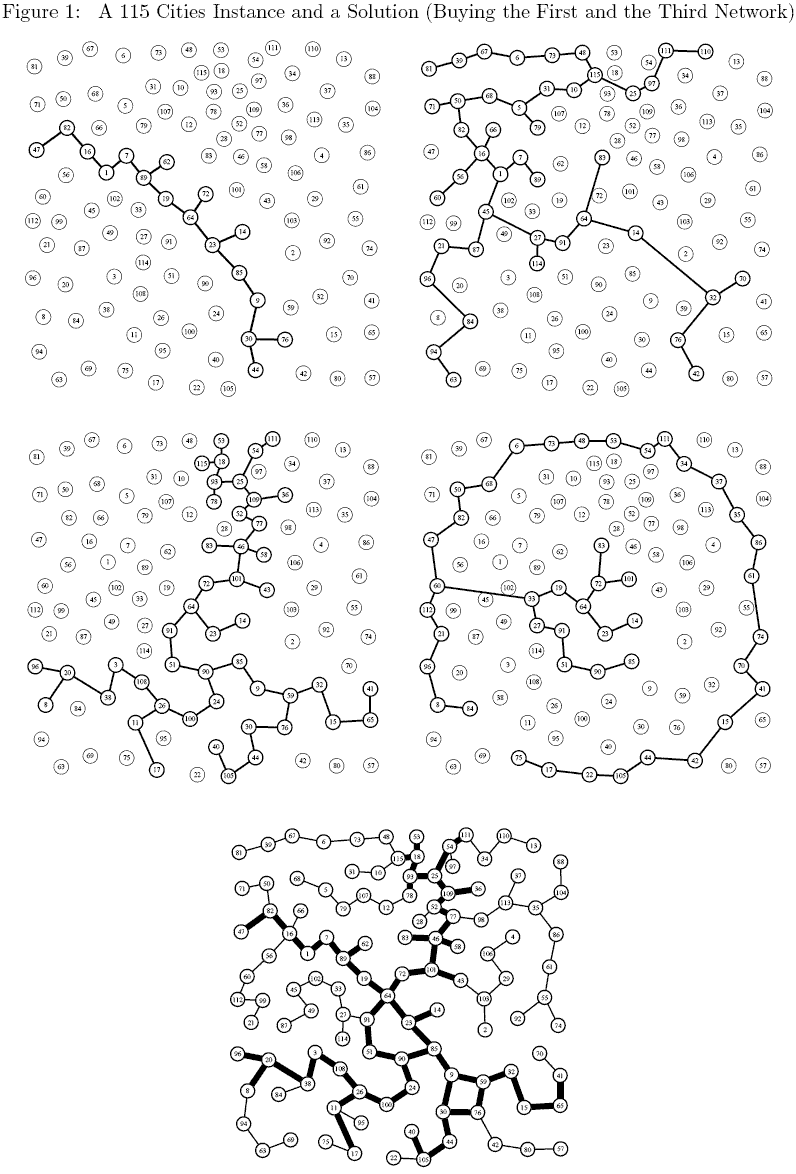
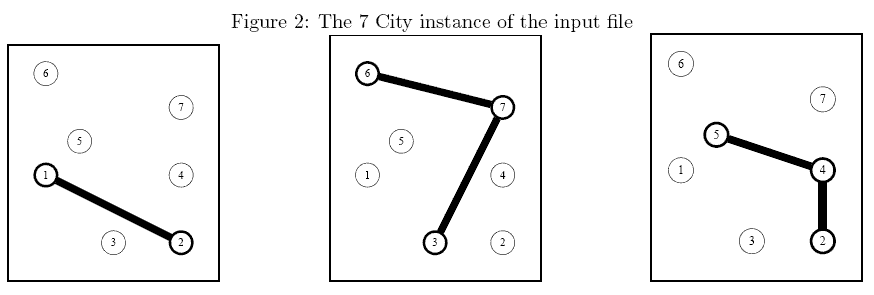
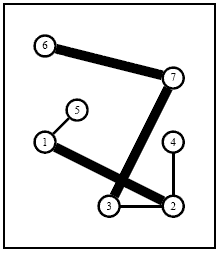
Source
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include<cmath> 6 #include<sstream> 7 #include<string> 8 using namespace std; 9 #define M 10000 10 int t,n,m,k,num; 11 int root[10005]; 12 struct Node 13 { 14 int x; 15 int y; 16 }; 17 Node node[1005]; 18 struct Buy 19 { 20 int a[10005]; 21 int cost; 22 int k; 23 }; 24 Buy buy[10005]; 25 int vis[10005]; 26 struct Edage 27 { 28 int u; 29 int v; 30 int len; 31 bool operator<(const Edage &a)const 32 { 33 return len<a.len; 34 } 35 }; 36 Edage edage[1000005]; 37 int cal(int a,int b) 38 { 39 int dis=(node[a].x-node[b].x)*(node[a].x-node[b].x)+(node[a].y-node[b].y)*(node[a].y-node[b].y); 40 return dis; 41 } 42 void add_edage(int a,int b) 43 { 44 edage[num].u=a; 45 edage[num].v=b; 46 edage[num].len=cal(a,b); 47 num++; 48 } 49 void init() 50 { 51 for(int i=1;i<=n;i++) 52 root[i]=i; 53 } 54 int fi(int x) 55 { 56 int k,j,r; 57 r=x; 58 while(r!=root[r]) 59 r=root[r]; 60 k=x; 61 while(k!=r) 62 { 63 j=root[k]; 64 root[k]=r; 65 k=j; 66 } 67 return r; 68 } 69 void uni(int a,int b) 70 { 71 int x=fi(a); 72 int y=fi(b); 73 if(x!=y) 74 root[x]=y; 75 76 } 77 int kruskal() 78 { 79 int ans=0; 80 int cnt=0; 81 for(int i=0;i<num;i++) 82 { 83 int x=fi(edage[i].u); 84 int y=fi(edage[i].v); 85 if(x!=y) 86 { 87 root[x]=y; 88 ans+=edage[i].len; 89 cnt++;} 90 if(cnt==n-1) 91 break; 92 } 93 return ans; 94 } 95 void solve() 96 { 97 init(); 98 int ans=kruskal(); 99 //int all=0; 100 for(int i=0;i<(1<<m);i++) 101 { 102 init(); 103 int all=0; 104 for(int j=0;j<m;j++) 105 { 106 if(!((i>>j)&1)) 107 continue; 108 for(int k=0;k<buy[j].k-1;k++) 109 uni(buy[j].a[k],buy[j].a[k+1]); 110 all+=buy[j].cost; 111 } 112 ans=min(ans,all+kruskal()); 113 } 114 printf("%d\n",ans); 115 } 116 int main() 117 { 118 scanf("%d",&t); 119 while(t--) 120 { 121 num=0; 122 memset(vis,0,sizeof(vis)); 123 scanf("%d%d",&n,&m); 124 for(int i=0;i<m;i++) 125 { 126 scanf("%d%d",&buy[i].k,&buy[i].cost); 127 for(int j=0;j<buy[i].k;j++) 128 scanf("%d",&buy[i].a[j]); 129 } 130 for(int i=1;i<=n;i++) 131 scanf("%d%d",&node[i].x,&node[i].y); 132 133 for(int i=1;i<=n;i++) 134 for(int j=i+1;j<=n;j++) 135 add_edage(i,j); 136 sort(edage,edage+num); 137 solve(); 138 if (t) puts(""); 139 140 } 141 142 return 0; 143 } 144 //1 145 // 146 //7 3 147 //2 4 1 2 148 //3 3 3 6 7 149 //3 9 2 4 5 150 //0 2 151 //4 0 152 //2 0 153 //4 2 154 //1 3 155 //0 5 156 //4 4
标签:
原文地址:http://www.cnblogs.com/ZP-Better/p/4642290.html