标签：
首先我们移动一下项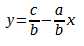
，并强行让a>b。
然后我们可以画出这样一个图像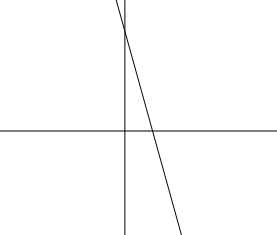
我们发现，在线段l与x轴交点处的下方，x，y的绝度值是递增的，所以我们不考虑那个最小点在下端。
之后我们发现在点的上端，因为斜率小于-1，x的减少远没有y加的快，所以我们知道极点在l与x轴的交汇处。
但是该点不一定是整点啊。。
所以我们只要找到它上面和下面最近的两个整点即可。
所以我们求ax+by=c最小的正整数解y即可，之后调出x，然后y减去a，再求x，比较两次min(|x|+|y|)，就可以得出答案了。
当然如果第一次求出来的y=0，答案就是它了。。
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<cmath> 5 6 #define ll long long 7 8 using namespace std; 9 10 ll gcd(ll a,ll b) 11 { 12 return b==0?a:gcd(b,a%b); 13 } 14 15 ll x,y; 16 17 void exgcd(ll n,ll m) 18 { 19 if(m==0){x=1,y=0;return;} 20 exgcd(m,n%m);ll t=x; 21 x=y;y=t-n/m*y; 22 } 23 24 int main() 25 { 26 ll a,b,d; 27 scanf("%lld%lld",&a,&b); 28 ll gd=gcd(a,b); 29 a/=gd,b/=gd; 30 exgcd(a,b); 31 while(~scanf("%lld",&d)) 32 { 33 if(d%gd){printf("BeiJu!\n");continue;} 34 d/=gd; 35 ll ans1=(y*d%a+a)%a,ans; 36 ans=abs(ans1)+abs((d-ans1*b)/a); 37 if(!ans1){printf("%lld\n",ans);return 0;} 38 ans1-=a; 39 ans=min(ans,abs(ans1)+abs((d-ans1*b)/a)); 40 printf("%lld\n",ans); 41 } 42 return 0; 43 }
代码略丑。。题目给出a，b，给出一堆c，求min(|x|+|y|).
关于ax+by=c的解x，y的min(|x|+|y|)值问题
标签：
原文地址：http://www.cnblogs.com/tuigou/p/4644057.html
