标签:
区间dp, 属于dp的一种,顾名思义,便是对区间处理的dp,其中石子归并,括号匹配,整数划分最为典型。
(1)石子归并
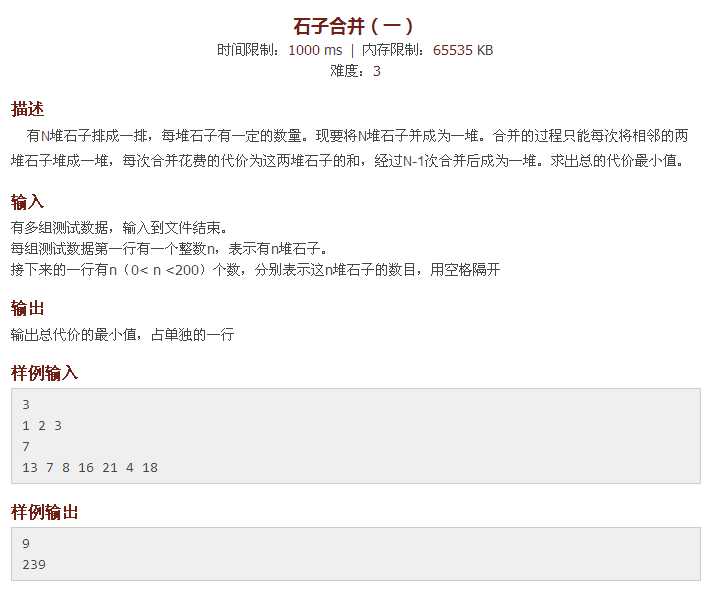
dp三要素:阶段,状态,决策。
首先我们从第i堆石子到第j堆石子合并所花费的最小费用设为dp[i][j], 然后去想状态转移方程,dp[i][j]必然有两堆石子合并而来, 那么我们很快就可以退出状态转移方程为dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j] + s);(s为两堆石子的总和)
下面附上代码

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 const int N = 200 + 5; 6 int a[N], dp[N][N], n, sum[N]; 7 8 void work(){ 9 for(int l = 1; l <= n; l ++){ 10 for(int i = 1; i + l <= n; i ++){ 11 int j = i + l; 12 for(int k = i; k <= j; k ++){ 13 dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j] + sum[j] - sum[i-1]); 14 } 15 } 16 } 17 printf("%d\n", dp[1][n]); 18 } 19 20 int main(){ 21 while(scanf("%d", &n) == 1){ 22 memset(dp, 0x3f,sizeof(dp)); 23 for(int i = 1; i <= n; i ++){ 24 scanf("%d", a + i); 25 sum[i] = sum[i-1] + a[i]; 26 dp[i][i] = 0; 27 } 28 work(); 29 } 30 return 0; 31 }
当然还有变形题
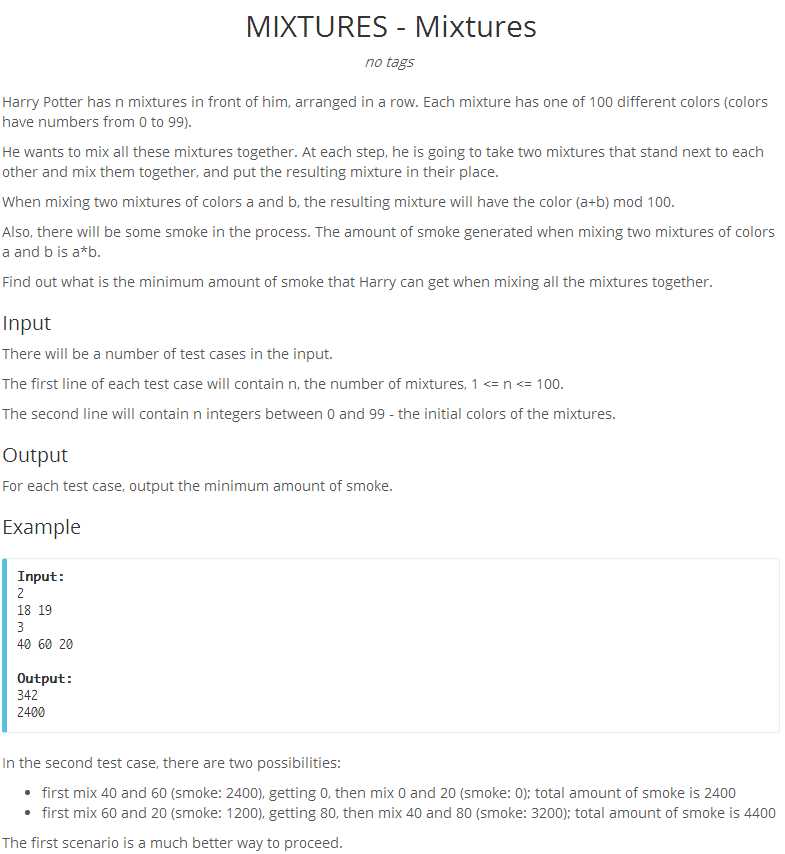
思路差不多只不过把两个数的和改成积(ps:在处理前缀和的时候千万别取余,否则可能出现负数)
附上代码:

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 const int N = 200 + 5; 6 int a[N], dp[N][N], n, ans, sum[N]; 7 8 void work(){ 9 for(int l = 2; l <= n; l ++){ 10 for(int i = 1; i <= n - l + 1; i ++){ 11 int j = i + l - 1; 12 for(int k = i; k < j; k ++){ 13 dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j] + ((sum[j] - sum[k])%100)*((sum[k] - sum[i-1])%100)); 14 } 15 } 16 } 17 printf("%d\n", dp[1][n]); 18 } 19 20 int main(){ 21 while(scanf("%d", &n) == 1){ 22 for(int i = 1; i <= n; i ++) 23 for(int j = 1; j <= n; j ++) 24 dp[i][j] = (1 << 30); 25 for(int i = 1; i <= n; i ++){ 26 scanf("%d", a + i); 27 sum[i] = sum[i-1] + a[i]; 28 dp[i][i] = 0; 29 } 30 work(); 31 } 32 return 0; 33 }
(2)括号匹配

这题解释括号匹配的例题,只要找到这个字符串中括号最大匹配量t,就可以得出答案,设长度为l,则ans = l - t;
我们设dp[i][j] 为第i位到第j位最大的括号匹配量, 则他的转移方程为
dp[i][j] = max(dp[i][j], dp[i][k] + dp[k+1][j]);
当然如果第i位刚好与第j位刚好匹配
则dp[i][j] = dp[i+1][j-1] + 2;
下面附上代码

1 #include <cstdio> 2 #include <iostream> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 7 string s; 8 9 int n, dp[105][105]; 10 11 int main(){ 12 int T; 13 scanf("%d", &T); 14 while(T--){ 15 cin >> s; 16 memset(dp, 0, sizeof(dp)); 17 for(int l = 0; l < s.size(); l ++){ 18 for(int i = 0; i + l < s.size(); i ++){ 19 int j = i + l; 20 if(s[i] == ‘(‘ && s[j] == ‘)‘) 21 dp[i][j] = dp[i+1][j-1] + 2; 22 if(s[i] == ‘[‘ && s[j] == ‘]‘) 23 dp[i][j] = dp[i+1][j-1] + 2; 24 for(int k = i; k <= j; k ++){ 25 dp[i][j] = max(dp[i][j], dp[i][k] + dp[k+1][j]); 26 } 27 } 28 } 29 printf("%d\n", s.size() - dp[0][s.size()-1]); 30 } 31 return 0; 32 }
(3)整数划分
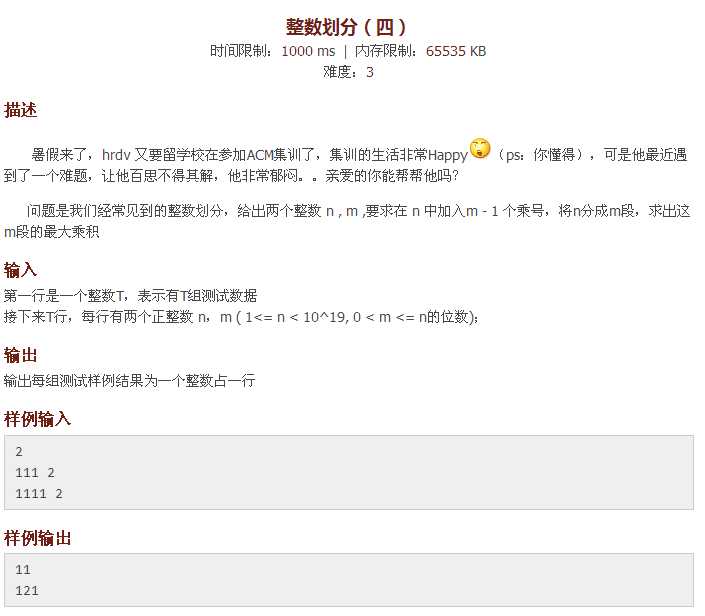
当初一看到这一题的时候感觉像是搜索题,仔细一想才明白是一道区间dp题,既然是dp,当然要先找到状态了,设dp[i][j]为前i位中存在j个乘号
我们以a[i][j]表示第i位到第j位的值,则可以推出状态转移方程为dp[i][j] = max(dp[i][j], dp[i][k] * a[k+1][j]);
附上代码

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 typedef long long ll; 6 const int N = 100 + 5; 7 8 ll a[N][N], dp[N][N]; 9 int n, T, c[N]; 10 char s[N]; 11 12 void work(){ 13 for(int j = 0; j < n; j ++){ 14 for(int i = 1; i <= strlen(s); i ++){ 15 for(int k = 1; k <= i; k ++){ 16 if(j==0) 17 dp[i][0] = a[1][i]; 18 else 19 dp[i][j] = max(dp[i][j], dp[k][j-1] * a[k+1][i]); 20 /*for(int p = 1; p <= strlen(s); p ++){ 21 for(int q = 0; q < n; q ++) 22 printf("%d ", dp[p][q]); 23 puts(""); 24 }*/ 25 } 26 } 27 } 28 printf("%lld\n", dp[strlen(s)][n-1]); 29 } 30 31 int main(){ 32 scanf("%d", &T); 33 while(T--){ 34 scanf("%s%d" , s, &n); 35 int flag = 0; 36 if(n > strlen(s)){ 37 printf("0\n"); 38 continue; 39 } 40 memset(a, 0, sizeof(a)); 41 memset(dp, 0, sizeof(dp)); 42 for(int i = 0; i < strlen(s); i ++) 43 c[i+1] = s[i] - ‘0‘; 44 for(int i = 1; i <= strlen(s); i ++){ 45 for(int j = i; j <= strlen(s); j ++){ 46 a[i][j] = a[i][j-1] * 10 + c[i]; 47 } 48 } 49 } 50 /*for(int i = 1; i <= strlen(s); i ++){ 51 for(int j = i; j <= strlen(s); j ++) 52 printf("%I64d ", a[i][j]); 53 puts(""); 54 }*/ 55 work(); 56 } 57 return 0; 58 }
标签:
原文地址:http://www.cnblogs.com/zyf0163/p/4645923.html