标签:
Given a large array of non-negative integer numbers, write a function which determines whether or not there is a number that appears in the array more times than all other numbers combined. If such element exists, function should return its value; otherwise, it should return a negative value to indicate that there is no majority element in the array.
Example: Suppose that array consists of values 2, 6, 1, 2, 2, 4, 7, 2, 2, 2, 1, 2. Majority element in this array is number 2, which appears seven times while all other values combined occupy five places in the array.
Keywords: Array, searching, majority, vote.
This problem can be viewed as the task of counting votes, where number of candidates is not determined in advance. Goal is to see if any of the candidates has collected more than half of all votes.
We could approach the problem in several ways. For example, we could sort the array and then simply count how many times each candidate appears. Since all occurrences of one value in sorted sequence are consecutive, determining the winner would be very simple. Here is the pseudo-code:
function FindMajoritySort(a, n) a - unsorted integer array n - number of elements in the array begin SortArray(a, n) -- use external function for sorting winner = -1 winCount = 0 curCount = 0 for i = 0, n - 1 begin if a[i] = cur then curCount = curCount + 1 else if curCount > winCount then winner = a[i - 1] winCount = curCount curCount = 1 else curCount = 1 end if curCount > winCount begin winner = a[n - 1] winCount = curCount end if winCount <= n - winCount then winner = -1 return winner end
This function is very efficient once the array is sorted. However, sorting the array takes time - O(NlogN) in general - and that will be the overall time complexity of this solution.
We might tackle the time complexity problem by somehow indexing the values while traversing the array. As long as data structure used to keep the counters runs in less than O(logN) time per read or write operation, we will be fine. And really, there is such a structure: hash table takes O(1) time to store a value or to find it. Here is the pseudo-code of the solution which relies on hash table to count how many times each element occurs in the array:
function FindMajorityHash(a, n) a - unsorted integer array n - number of elements in the array begin hashtable -- used to index counts for each value winner = -1 for i = 0, n - 1 begin count = 1 if hashtable.Contains(a[i]) then count = hashtable(a[i]) + 1 hashtable(a[i]) = count if winner < 0 or count > hashtable(winner) then winner = a[i] end if 2 * hashtable(winner) <= n then winner = -1 return winner end
This function runs in O(N) time, but suffers a problem of a different sort. It requires additional space for the hash table, which is proportional to N. For a very large array, this may be a serious obstacle.
By this point we have devised one solution which runs in O(NlogN) time and O(1) space; another solution runs in O(N) time and O(N)space. Neither of the two is really good. It would be beneficial if we could devise a solution that takes good parts of both, i.e. a solution that runs in constant space and completes in time that is proportional to length of the array. We will try to construct a solution that runs in O(N) time and O(1) space.
We could run through the array and let that number outperform all other numbers. For instance, whenever we encounter value M in the array, we would increment some counter. On any other value, we would decrement the counter. Current value stored in the counter is the information which survives during the array traversal. It would go up and down, or might even be negative sometimes. But when end of the array is reached, value in the counter will definitely be positive because there was more increment than decrement operations. Figure below shows an example in which we are proving that number 1 is the majority value in an array.
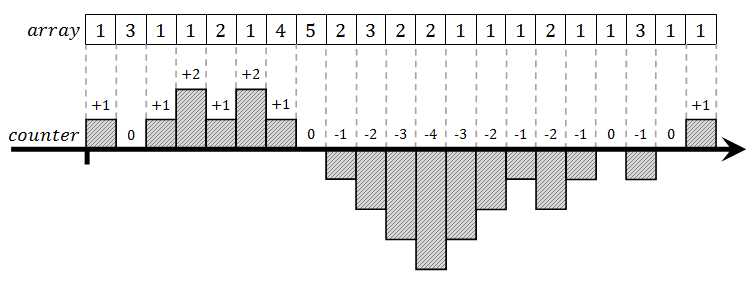
When this modified solution is applied to the whole array, we end up with a number which is the last majority candidate. We are still not sure whether this number is overall majority element of the array or not. But the selection process adds some qualities to that candidate. Let‘s observe the previous array when processed by this new algorithm.
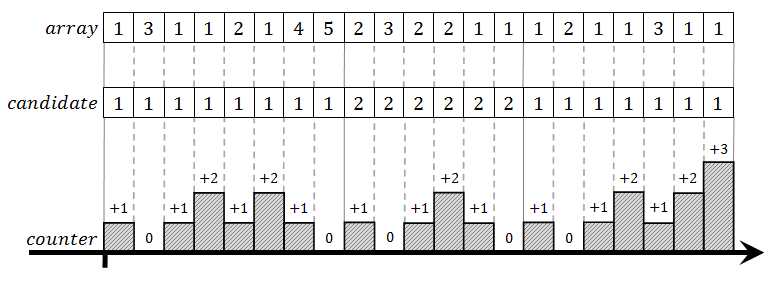
This time counter never goes into negative. It always bounces off the zero value and turns back into positive range, at the same time switching to the new majority candidate. The whole process now divides the array into segments. In each segment one number occurs as many times as all other numbers combined. In the worst case, those "all other numbers" will actually be a single number which occurs as many times as the candidate for that segment - we don‘t know whether that is the case or not, because we are counting only the candidate’s occurrences.
Anyway, when all segments align, the last segment alone decides the battle, and here is why. All segments except the last one look the same. First number in the segment is the special element and it occurs as many times as all other numbers in the segment combined. We know this fact because every segment ends with counter equal to zero (this is what candidate selection process guarantees). So all segments but the last one together are guaranteed not to contain a majority element. At best, there will be one number that occurs as many times as all the others combined, but not more than that. The only number that really could be the majority element of the array is the winner of the last segment, i.e. final majority candidate that remains when end of array is reached.
This complete solution requires a couple of variables to store current candidate and the counter. It passes the array once or twice. In the first pass, majority candidate is established. In the second pass we simply check whether the candidate is a solution or there is no majority element. This means that algorithm described runs in O(N) time and O(1) space.
Implementation will consist of two functions. First one will count occurrences of a number, subtracting other elements from the count. Majority element will be the value for which this function returns positive result. Another function will establish the majority candidate and then call the first function to decide whether it is the majority element or there is no majority element in the array. Here is the pseudo-code:
function GetCountForValue(a, n, x) a - array of non-negative integers n - number of elements in the array x - number for which count is required begin count = 0 for i = 0, n-1 begin if a[i] = x then count = count + 1 else count = count - 1 end return count end function FindMajorityElement(a, n) a - array of non-negative integers n - number of elements in the array begin count = 1 candidate = a[0] for i = 1, n-1 begin if a[i] = candidate then count = count + 1 else if count = 0 then candidate = a[i] count = 1 else count = count – 1 end if count > 0 then count = GetCountForValue(a, n, candidate) if count > 0 then return candidate return -1 -- there is no majority element end
Below are functions GetCountForValue and FindMajorityElement, coded in C#. The code is relatively simple, once all the analysis has been provided.
static int GetCountForValue(int[] a, int x) { int count = 0; for (int i = 0; i < a.Length; i++) if (a[i] == x) count++; else count--; return count; } static int FindMajorityElement(int[] a) { int count = 1; int candidate = a[0]; for (int i = 1; i < a.Length; i++) { if (a[i] == candidate) { count++; } else if (count == 0) { candidate = a[i]; count = 1; } else { count--; } } if (count > 0) count = GetCountForValue(a, candidate); if (count > 0) return candidate; return -1; }
Quote From:
标签:
原文地址:http://www.cnblogs.com/liao-hua/p/4646975.html