暑假到了!!小Hi和小Ho为了体验生活,来到了住在大草原的约翰家。今天一大早,约翰因为有事要出去,就拜托小Hi和小Ho忙帮放牧。
约翰家一共有N个草场,每个草场有容量为W[i]的牧草,N个草场之间有M条单向的路径。
小Hi和小Ho需要将牛羊群赶到草场上,当他们吃完一个草场牧草后,继续前往其他草场。当没有可以到达的草场或是能够到达的草场都已经被吃光了之后,小hi和小Ho就把牛羊群赶回家。
一开始小Hi和小Ho在1号草场,在回家之前,牛羊群最多能吃掉多少牧草?
举个例子:
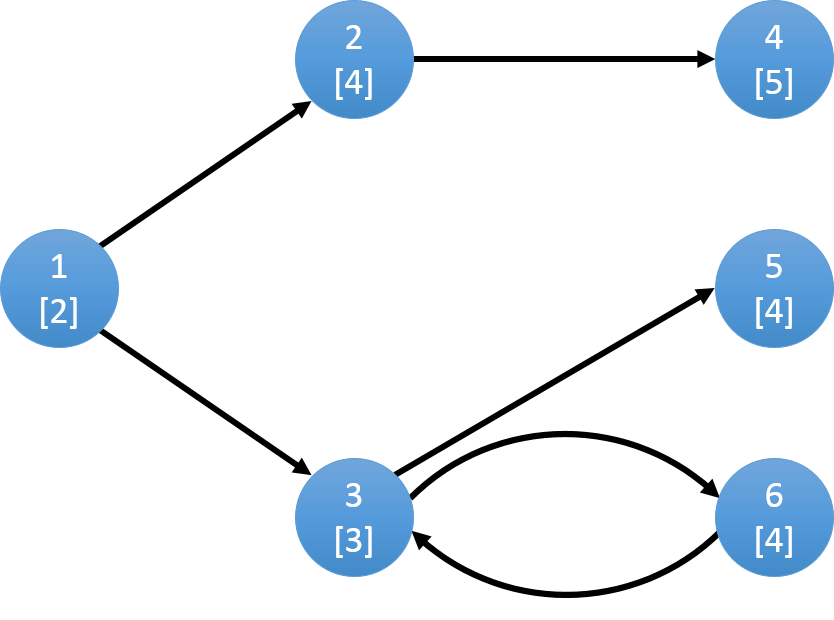
图中每个点表示一个草场,上部分数字表示编号,下部分表示草场的牧草数量w。
在1吃完草之后,小Hi和小Ho可以选择把牛羊群赶到2或者3,假设小Hi和小Ho把牛羊群赶到2:
吃完草场2之后,只能到草场4,当4吃完后没有可以到达的草场,所以小Hi和小Ho就把牛羊群赶回家。
若选择从1到3,则可以到达5,6:
选择5的话,吃完之后只能直接回家。若选择6,还可以再通过6回到3,再到5。
所以该图可以选择的路线有3条:
1->2->4 total: 11 1->3->5 total: 9 1->3->6->3->5: total: 13
所以最多能够吃到的牧草数量为13。
本题改编自USACO月赛金组
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2行:N个正整数,第i个整数表示第i个牧场的草量w[i]。1≤w[i]≤100,000
第3..M+2行:2个正整数,u,v。表示存在一条从u到v的单向路径。1≤u,v≤N
第1行:1个整数,最多能够吃到的牧草数量。
6 6 2 4 3 5 4 4 1 2 2 4 1 3 3 5 3 6 6 3
13
#include <iostream>
#include <vector>
#include <unordered_map>
#include <algorithm>
#include <queue>
using namespace std;
struct idTime{
int id; //结点id
int time; //结点结束访问时间
};
struct Cmp{
const bool operator()(const idTime &a, const idTime &b) const{
if(a.time != b.time) return a.time < b.time;
else return a.id < b.id;
}
};
//深度搜索有向图G,记录结束访问时间
void dfs1(int v, vector<int> ×, vector<int> &visited, vector<vector<int>> &edge, int &cur){
if(visited[v]) return;
visited[v] = 1;
for(int i = 0; i < edge[v].size(); i++)
if(!visited[edge[v][i]])
dfs1(edge[v][i], times, visited, edge, cur);
times[v] = cur;
cur++;
}
//深度搜索转置图Gt,记录访问的结点
void dfs2(int v, vector<int> &visited, vector<vector<int>> &edge, vector<int> &com){
if(visited[v]) return;
visited[v] = 1;
com.push_back(v);
for(int i = 0; i < edge[v].size(); i++)
if(!visited[edge[v][i]])
dfs2(edge[v][i], visited, edge, com);
}
//根据邻接表edge,求有向图G的强连通分量ret,算法参考《算法导论》
void SCC(vector<vector<int>> &ret, vector<vector<int>> &edge){
int n = edge.size();
if(n <= 1) return;
vector<int> times(n, 0);
vector<int> visited(n, 0);
int cur = 0;
//记录有向图G的各个结点在深度遍历时的结束访问时间
for(int i = 1; i < n; i++){
if(!visited[i])
dfs1(i, times, visited, edge, cur);
}
//for(int i = 1; i < times.size(); i++) cout << i << ": " << times[i] << endl;
//构造有向图G的转置图Gt
vector<vector<int>> reEdge(n, vector<int>());
for(int i = 1; i < n; i++){
for(int j = 0; j < edge[i].size(); j++)
reEdge[edge[i][j]].push_back(i);
}
for(auto &a : visited) a = 0;
//使用优先队列保存,队首保存结束访问时间最大的结点
priority_queue<idTime, vector<idTime>, Cmp> priQue;
for(int i = 1; i < times.size(); i++){
idTime tmp;
tmp.id = i;
tmp.time = times[i];
priQue.push(tmp);
}
while(1){
vector<int> com;
int maxId = -1;
//总是从队首取出未访问的结束访问时间最大的结点
while(!priQue.empty()){
if(visited[priQue.top().id]){
//cout << "pop: " << priQue.top().id << endl;
priQue.pop();
}
else{
//cout << "maxId: " << priQue.top().id << endl;
maxId = priQue.top().id;
break;
}
}
if(maxId == -1) break;
//以未访问的结束访问时间最大的结点,深度遍历转置图Gt,得到一个强连通分量com
dfs2(maxId, visited, reEdge, com);
ret.push_back(com);
}
}
//回溯深度遍历有向图G',更新访问路径经过结点的权值和的最大值
void dfs3(int v, vector<vector<int>> &edge, vector<int> &visited, vector<int> w, int &maxV, int cur){
if(visited[v]) return;
cur += w[v];
maxV = max(maxV, cur);
visited[v] = 1;
//cout << edge[v].size() << endl;
for(int i = 0; i < edge[v].size(); i++){
//cout << visited[edge[v][i]] << endl;
if(!visited[edge[v][i]])
dfs3(edge[v][i], edge, visited, w, maxV, cur);
}
visited[v] = 0;
}
//算法时间复杂度为O(VlgV+E),空间复杂度O(E+V)
int main(void){
#ifndef ONLINE_JUDGE
freopen("d://file.in", "r", stdin);
#endif // ONLINE_JUDGE
int N, M;
cin >> N >> M;
vector<int> w(N+1, 0); //权值
vector<vector<int>> edge(N+1, vector<int>()); //有向图G邻接表
for(int i = 1; i <= N; i++){
cin >> w[i];
}
for(int i = 0; i < M; i++){
int s, e;
cin >> s >> e;
edge[s].push_back(e);
}
vector<vector<int>> coms; //强连通分量
SCC(coms, edge);
/*for(auto a : coms){
for(auto b : a){
cout << " " << b;
}
cout << endl;
}*/
//根据强连通分量和连接表重构有向图G',对于每一个强连通分量,合为一个结点,假设即为u,
//结点u的权值为分量所有结点的权值和,结点u的边为与分量內结点与其他强连通分量连接的边
//有向图G'为DAG
int n = coms.size();
unordered_map<int, int> C; //有向图G结点id与强连通分量id(即有向图G'中结点)映射
vector<int> W(n, 0); //有向图G'中结点权值
for(int i = 0; i < n; i++){
for(auto a : coms[i]){
C[a] = i;
W[i] += w[a];
}
}
/*cout << endl;
for(auto itr = C.begin(); itr != C.end(); itr++) cout << itr->first << " " << itr->second << endl;
for(auto a : W) cout << " " << a;
cout << endl;*/
vector<vector<int>> EDGE(n, vector<int>()); //有向图G'邻接表
for(int i = 1; i <= N; i++){
for(auto a : edge[i]){
if(C[i] != C[a]){
//cout << C[i] << "->" << C[a] << endl;
EDGE[C[i]].push_back(C[a]);
}
}
}
/*cout << endl;
for(int i = 0; i < n; i++){
cout << i << ": ";
for(auto a : EDGE[i]){
cout << " " << a;
}
cout << endl;
}
cout << endl;*/
int maxV= 0;
vector<int> visited(n, 0);
//深度遍历有向图G'找到最大权值和
dfs3(C[1], EDGE, visited, W, maxV, 0);
cout << maxV << endl;
return 0;
}
版权声明:本文为博主原创文章,未经博主允许不得转载。
原文地址:http://blog.csdn.net/u011863942/article/details/46908263