标签:
tail recursion, 顾名思议,就是将递归放到函数的尾部,说到它的不一样,就得先说说一般的递归。对于一般的递归,比如下面的求阶乘,教科书上会告诉我们,如果这个函数调用的深度太深,很容易会有爆栈的危险。
int Factorial(int n){if(n < 0) { return 0; }else if(n == 1) { return 1; }else { return n * Factorial(n - 1); }}
该函数调用的大致过程
1)调用开始前,调用方(或函数本身)会往栈上压相关的数据,参数,返回地址,局部变量等。
2)执行函数。
3)清理栈上相关的数据,返回。
因此,在函数 A 执行的时候,如果在第二步中,它又调用了另一个函数 B,B 又调用 C.... 栈就会不断地增长不断地装入数据,
当这个调用链很深的时候,栈很容易就满 了,这就是一般递归函数所容易面临的大问题。
而尾递归在某些语言的实现上,能避免上述所说的问题,注意是某些语言上,尾递归本身并不能消除函数调用栈过长的问题,
那什么是尾递归呢?在上面写的一般递归函数 Factorial() 中,我们可以看到,Factorial(n) 是依赖于 Factorial(n-1) 的,Factorial(n) 只有在得到 Factorial(n-1) 的结果之后,
才能计算它自己的返回值,因此理论上,在 Factorial(n-1) 返回之前,func(n),不能结束返回。
因此Factorial(n)就必须保留它在栈上的数据,直到Factorial(n-1)先返回,而尾递归的实现则可以在编译器的帮助下,消除这个限制:
int FactorialTail(int n, int res){if(n < 0) return 0;else if(n == 0) return 1;else if(n == 1) return res;else return FactorialTail(n - 1, n * res);}
从上可以看到尾递归把返回结果放到了调用的参数里。这个细小的变化导致,FactorialTail(n, res)不必像以前一样,非要等到拿到了FactorialTail(n-1, n*res)的返回值,
才能计算它自己的返回结果 -- 它完全就等于FactorialTail(n-1, n*res)的返回值。因此理论上:FactorialTail(n)在调用FactorialTail(n-1)前,完全就可以先销毁自己放在栈上的东西。
这就是为什么尾递归如果在得到编译器的帮助下,是完全可以避免爆栈的原因:每一个函数在调用下一个函数之前,
都能做到先把当前自己占用的栈给先释放了,尾递归的调用链上可以做到只有一个函数在使用栈,因此可以无限地调用!
尾递归的调用栈优化特性
但是尾递归的实现依赖于编译器的帮助(或者说语言的规定)。
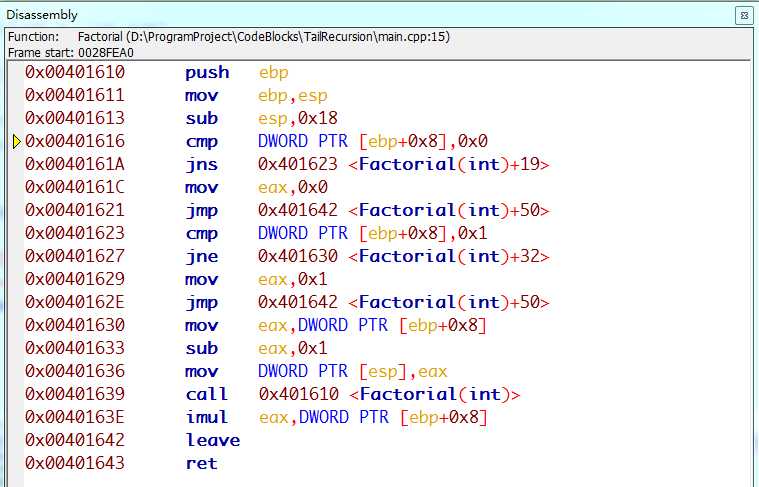
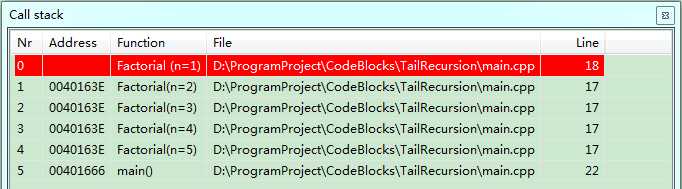
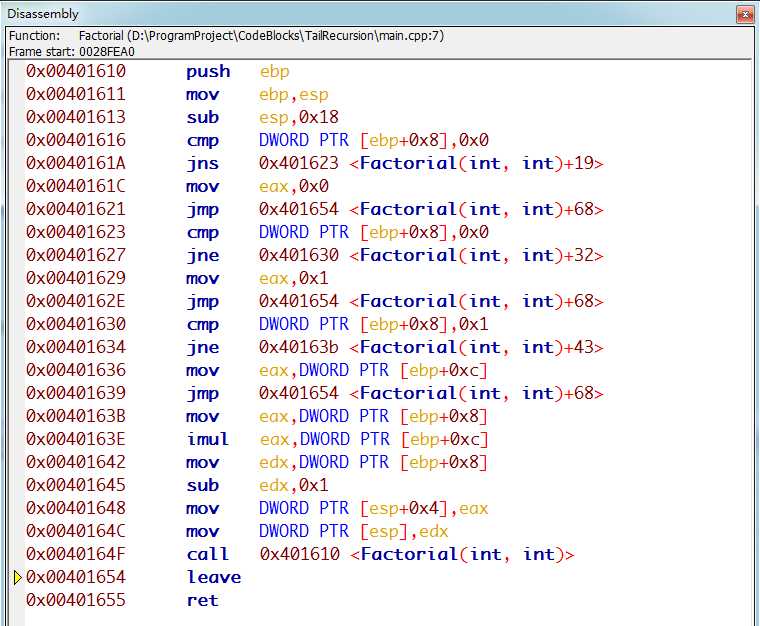
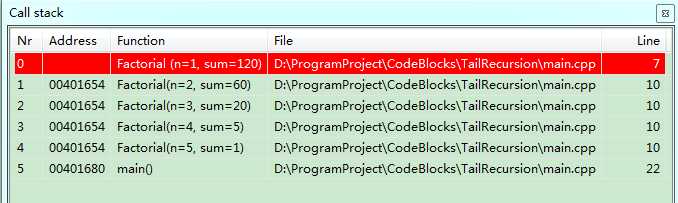
我在code:blocks开发环境中先后测试了这两个函数,分别显示了各自的汇编代码以及栈的调用情况。
测试的主函数如下:
int main(){cout << FactorialTail(5, 1) << endl;cout << Factorial(5) << endl;return 0;}
g++ -g -Wa,-adlhn hello.cpp > out.sg++ -O2 -g -Wa,-adlhn hello.cpp > out.s

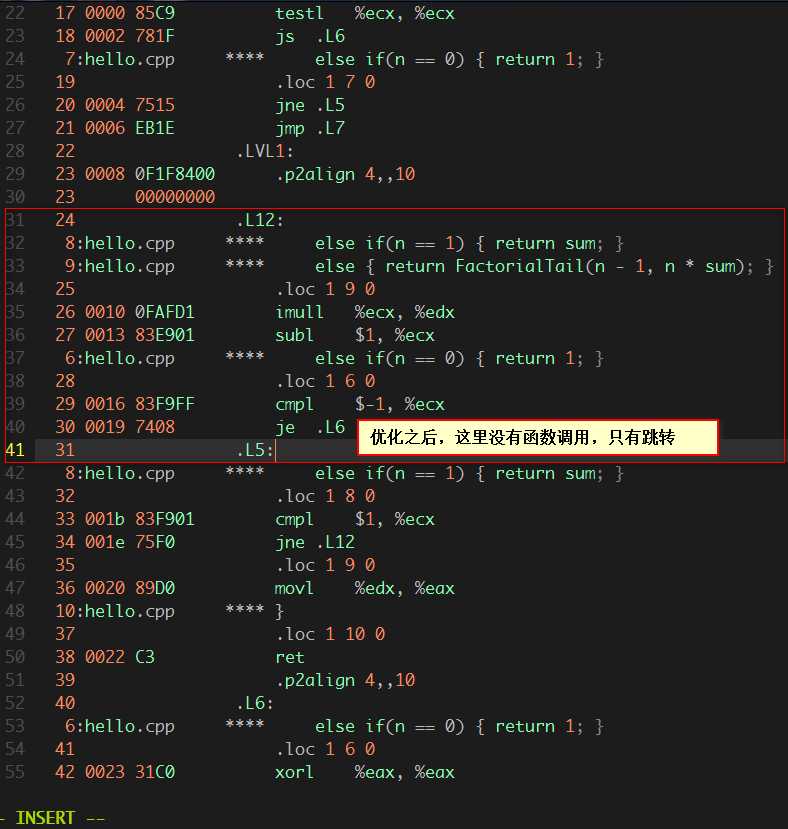
通过上述两个汇编代码可以看出,在开启了编译器优化之后,尾递归不用每次进行压栈操作,所有的递归都是在同一栈空间内进行的。
标签:
原文地址:http://www.cnblogs.com/fengkang1008/p/4652201.html