《有限元分析基础教程》（曾攀）笔记二-梁单元方程推导

标签：

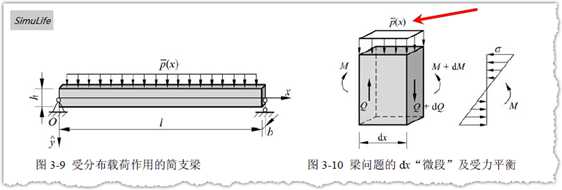
上图是《有限元分析基础教程》中的图。

这是《材料力学》（孙训方）里面给出的图。

    之所以给出这两幅图，是因为在推导公式的时候，第一幅图让我误解了：红箭头标注的微端中的外荷载$\bar{p(x)}$，看起来像是面荷载，实际推导公式的时候，$\bar{p(x)}$是个线荷载。由于两幅图中的一些符号不一致，我下面的推导均采用曾攀老师书中的符号，有的时候也将$\bar{p(x)}$简写成$\bar{p}$。

    我们取梁的挠度方程$v(x)$作为整个推导的基本量，同时也是整个推导的核心，所有的推导其实都是围绕这个$v(x)$来展开。至于为什么要将$v(x)$作为基本量，按照我个人的理解：

1. 首先，对于梁，最关心当然是承受外力作用下的变形，也就是挠度沿着梁长度方向的变化规律，即$v(x)$。
2. 如果我们建立了挠度的微分方程$v(x)$，那么在梁的两端的挠度是已知的，也就是有非常明确的边界条件的。

    因为图中梁只受到外力荷载$\bar{p(x)}$的作用，所以建立挠度方程$v(x)$关键就是建立挠度$v(x)$与外荷载$\bar{p(x)}$之间的关系。这个关系的建立可以很直观的想到对于微段运用$Y$方向的合力平衡，即

\begin{equation}
(Q+dQ)+\bar{p(x)}-Q=0
\end{equation}

化简后，可以得到

《有限元分析基础教程》（曾攀）笔记二-梁单元方程推导

标签：

原文地址：http://www.cnblogs.com/SimuLife/p/4652633.html